О некоторых оценках для критерия начала фрагментации молекулярных ионов в электрогазодинамических полях

Взаимодействие ионов с молекулами газовой среды широко используется в современной масс-спектрометрии. Метод столкновительной ячейки оказался эффективным в получении информации о структуре молекул, а также в исследовании многокомпонентных смесей.

С возникновением масс-спектрометрии ЭРИАД (разновидности электроспрея, Еlectrospray Ionization — ESI) [1] появилась возможность управляемой фрагментации молекул в области совмещения газового потока и электрического поля (область электрогазодинамического поля) путем варьирования напряжения между соплом и скиммером системы ионообразования и формирования пучка ионов. Метод ЭРИАД с использованием управляемой фрагментации оказался перспективным в элементном и изотопном анализах [2].

Интерес к процессам фрагментации молекул в электрогазодинамических полях повысился в последнее время в связи с развитием исследований сложных биоорганических молекул (белки, протеины, липиды, углеводороды и т. д.) в системах, совмещающих спектрометр ионной подвижности и масс-спектрометр (Ion Mobility Spectrometry— Mass Spectrometry, IMS—MS) [3, 4].

Все эти новые тенденции в развитии экспериментальных методов исследования биоорганиче-ских молекул делают актуальным построение математических моделей процессов транспорта и фрагментации молекулярных ионов в электрогазодинамических полях различной структуры.

В настоящей статье рассматривается задача о критериях начала фрагментации молекулярных ионов в электрогазодинамических полях, образованных потоками спутного газа и электрическими полями, в условиях больших градиентов как газодинамических, так и электрических параметров.

1. ПОСТАНОВКА ЗАДАЧИ

Хорошо известно, что скорости ионно-молекулярных реакций сильно зависят от величины электрического поля. Если предположить, что фрагментация молекулярного иона происходит, когда кинетическая энергия относительного движения, набираемая ионом на длине свободного пробега, превышает энергию связи E ₀ , то для величины напряженности электрического поля ε , начиная с которой эта связь начинает разрываться, получаем следующую оценку:

с ^ m + M EN. , (1)

Me где m и M — массы иона и молекулы спутного газа соответственно; N — число молекул в единице объема; σ — сечение столкновения иона с молекулой; e — величина элементарного заряда.

В данной оценке не учитывается распределение молекул и ионов по скоростям, которое в сильном электрическом поле может сильно отличаться от максвелловского. Не учитывается также энергетическая зависимость сечения фрагментации молекулярного иона. Кроме того, эта оценка выполнена для фрагментации в результате конкретного единичного столкновения. Нас же будут интересовать оценки для критерия фрагментации на определенном промежутке дрейфа.

В общем случае вероятность диссоциации (фрагментации) молекулярного иона, дрейфующего в буферном газе под действием электрического поля, определяется неравновесной функцией распределения иона по энергетическим состояниям [5]. Последняя является решением основного кинетического уравнения — линейного интегродиф-ференциального уравнения, описывающего изменение функции распределения по энергиям в результате мономолекулярного превращения [6]. Спутный газ при этом играет роль активатора. Решение этого уравнения представляется очень сложным и является основной задачей теории мо-номолекулярных реакций [7].

С целью получения простых зависимостей константы скорости диссоциации от напряженности электрического поля с учетом распределения ионов и молекул по скоростям представим процесс диссоциации в виде бимолекулярной реакции иона с молекулой спутного газа

A + + B ^ C + + D + B,(2)

константа скорости которой определяется в терминах функций распределения скоростей ионов и нейтральных молекул:

K = J f (Ui MUB )ad (Ur )Ur d3Uid3UB , где иr = иi — иB — скорость относительного движения;

. х ( м i

Ф(иB) = I I exp — ^-TB I —(4)

V 2 nkT )     V 2 kT )

максвелловская функция распределения молекул по скоростям; f ( υ _i ) — неизвестная функция распределения ионов по скоростям; σ_d ( υ_r ) — сечение диссоциации.

Для модели твердой сферы взаимодействия иона с молекулой газа ( a = const) безразмерным параметром задачи является отношение энергии, набираемой ионом на длине свободного пробега, пропорциональной отношению ε N (размерному параметру, принятому в теории подвижности ионов в газах [8]), к тепловой энергии молекул газа:

5 = ^ hr- .           (5)

Nσ

Для модели Максвелла (среднее время между столкновениями т = const) таким параметром является отношение энергии, набираемой ионом за время свободного пролета τ , пропорциональное ( ε N )² , к тепловой энергии молекул газа

5 = ке;;П 1_кт .                (6)

2 m

Основной вклад в интеграл (3) при достаточно больших значениях параметра δ дает область изменения направления скорости иона вблизи направления напряженности электрического поля ε . Поэтому в качестве функции распределения f ( υ _i ) в выражении (3) можно взять асимптотическое решение уравнения Больцмана для ионов в сильном поле, полученное в работе [9] (см. также [10]) для различных моделей сечения взаимодействия ионов с молекулами газа.

1. Для модели твердой сферы ( с = const):

f ^{( и )} =

32     12

m | [ 1 |

2nkT ) V 5 )

x exp <

x

m ^{( u} X ⁺ ^

2 kT

1 mυ_z ² δ 2 kT

^ 29(u_z ),

θ ( υ_z ) — функция Хевисайда.

2. Для модели Максвелла, в которой σ ~ 1 υ_r и среднее время между столкновениями т =

= ( Nu r a ) ^{- 1} = const:

^{f ( u} z ) JJ ^{f ( u )d u} x ^{d u} y =

m I mu   mkT

----exp <--- +------ 2

2 еет    [ еет 2( еет )

В формулах (7) и (8) ось Z выбрана вдоль направления поля ε .

2. КОНСТАНТА СКОРОСТИ ДИССОЦИАЦИИ И ЧИСЛО ФРАГМЕНТИРУЮЩИХ СТОЛКНОВЕНИЙ. ОСНОВНЫЕ ОЦЕНКИ

Рассмотрим случай a = const. Подставляя распределения (4) и (7) в формулу (3) и проводя интегрирование по скоростям молекулы газа, получаем:

к = ^ 2 πkT

-^- I x V 2 nkT )

^x J ^d 3 ^{u e}xp <

—

ц ^{( и} Х ^{+ и 2)}

2 kT

—

µυ_z ²

2 kT_i

^{> ua} d ^{( u} ),

mM где ц =--приведенная масса.

m + M

В формуле (9) введена эффективная ионная температура

T = m f T + M e ^£ ‘ m + M ( m Nok

=        /'I1 + M 5 I, m + M I m )

учитывающая вклад электрического поля в кинетическую энергию иона.

При больших значениях параметра δ (сильное поле) можно считать, что скорость иона направлена вдоль оси Z и и = ^иХ + uy + uZ ~ uz . Проведя в выражении (8) интегрирование по переменным υx и υy , получаем к =----1—йт fdEo(E)expf" — I    (11)

( 2n^kT, )^v 2 j      d ¹ kT, )

В качестве сечения диссоциации σ_d ( E ) возьмем выражение, обычно используемое для сечения реакции, имеющей энергетический порог [11]:

n = (v ( s ) d ⁵ = ^Z' N ( s)к(s ) d s ,        (16)

z ^J ₀        U d ( s )     J               U d ( s )’          ' '

где v = N к — частота фрагментирующих столкновений, υ_d — скорость дрейфа ионов в газе под действием электрического поля.

В случае сильного поля, когда 5 >>  1 и эффективная температура (10) в основном определяется величиной поля

T ~ M   ее i m + M kN о ’ а для величины дрейфовой скорости можно взять соотношение [8]

1 ( µM )¹⁴

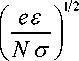
используя соотношение (15) для константы скорости фрагментирующих столкновений, из выражения (16) получаем od (E) = °0(1 - E0IE)V при E > E0 и od (E) = 0           при E < E0,

n = о

( µM )¹⁴ (2 πm )^{1 2}

x

где E ₀ — энергетический порог реакции.

Тогда интегрирование в выражении (11) может быть проведено до конца, и константа скорости диссоциации выразится через вырожденную гипергеометрическую функцию T ( a , b , z ) [12]:

Z        [ m + M E₀N ( s ) o 1

N ( s )exp ^----- 0-^т²- ^ d s .

Z ₀           I ^{M     е е ( s} )

Eσ

К = ------ 0 0 1 /7 ^x

( 2n^kT ) ¹²

x Г (1 + v ) T (1 + v , 2, E ₀ / kT )exp

k

E 0

kT

Фактор exp( - E ₀ JkTi ) соответствует фактору Аррениуса—Больцмана в равновесной кинетике [11]. Он содержит в отличие от классической формулы эффективную температуру, зависящую от напряженности электрического поля.

В качестве условия начала фрагментации можно принять условие n >  1. Это условие вместе с выражением (17) решает в принципе задачу об определении порогового значения величины электрического поля, начиная с которого происходит разрыв связи с энергией связи E ₀ на промежутке ( z ₀ , z ) , если известны пространственные распределения концентрации молекул газа N ( z ) и электрического поля ε ( z ) .

Рассмотрим случай v = 0 , означающий, что в качестве сечения диссоциации взята "ступенчатая" функция

o d = о ₀, при E >  E ₀ и o_d = 0 при E <  E ₀.   (14)

Тогда

• 2.    ЧАСТНЫЕ СЛУЧАИ

  • 2.1.    Свободно расширяющаяся газовая струя, однородное электрическое поле

Согласно этим условиям,

N ^{( z} ) = AN 0 ^{( d} */ ^{z ) 2} при ^z >  ^z 0 ,       (18)

• е( z ) = const.

f kT, V ^к = ^о о I ~I ^exP

^ 2пц )

- -0- I . I kTJ

Число фрагментирующих столкновений на промежутке ( z ₀ , z )

В качестве значения z ₀ берут расстояние от критического сечения сопла (диаметр d * ), начиная с которого истечение газа соответствует истечению из точечного источника, обычно z ₀ ® 3 d * [13].

В этом случае число фрагментирующих столк-

новений, вычисленное по формуле (17), может быть выражено через функцию ошибок:

n = О о

Ц 34 M  ^f ee N ⁽ z 0 ) z 02 T _х

величины электрического поля, ни от энергии связи. Соотношения (20) и (21) соответствуют (с точностью до множителя) простой оценке числа столкновений с фрагментацией

2 m

( E о    2o

^Х { ^{Ф (} a ) ^{-ф (} az 0 / z ) } ,

где a =

m + M E 0 N ( z ₀) o Y2

E ₀

z ds n = zJ0 M s)

z

= J N (s )o 0ds = z0

M

eε

I ^ИАz о ) )

,

z

z

= AN 0 dО 0/- = о 0 N ( z 0 ) z 0 1 1 - z 0 ^{s                   V}

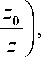
При a <<  1, что соответствует приближению очень сильного поля, получаем

( цМ )^v 4           f z ₀ )

n = ^О 0        12 N ^{( z} 0 ) ^z 0 1 ¹-- I ,

(2nm )'            V z )

или

( µM )¹⁴

n = о ₀       12

(2 πm )^{1 2}

N ( z 0 ) z°- A = ^{( цМ} ^ z A A , z     (2 πm )^{1 2} z λ ₀

где z = z ₀ + A , A₀ = ( N ( z ₀ ) o ₀ ) ¹ — длина свободного пробега по отношению к фрагментации в начальной области струи.

Отметим, что в этом случае n не зависит ни от в которой не учитывается скоростное распределение как молекул газа, так и фрагментирующих ионов.

Подобное асимптотическое поведение числа фрагментирующих столкновений на промежутке дрейфа в свободно расширяющейся струе подтверждается результатами компьютерного моделирования. Они представлены на рисунке, где приведены рассчитанные методом статистического моделирования гистограммы распределения координаты точки фрагментации для ряда значений напряженности электрического поля.

Значения остальных параметров: масса молекулы иона m = 100 а.е.м.; масса молекулы газа M = = 28 а.е.м.; диаметр критического сечения газовой струи d * = 0.2 см; z 0 = 0.6 см; N ( z 0 ) = 2∙10¹⁶ см^–3; kT ( z ₀) = 0.02 эВ; о = 10 ^{- 15} см². Для указанных значений параметров и при e = 2000 В/см получаем

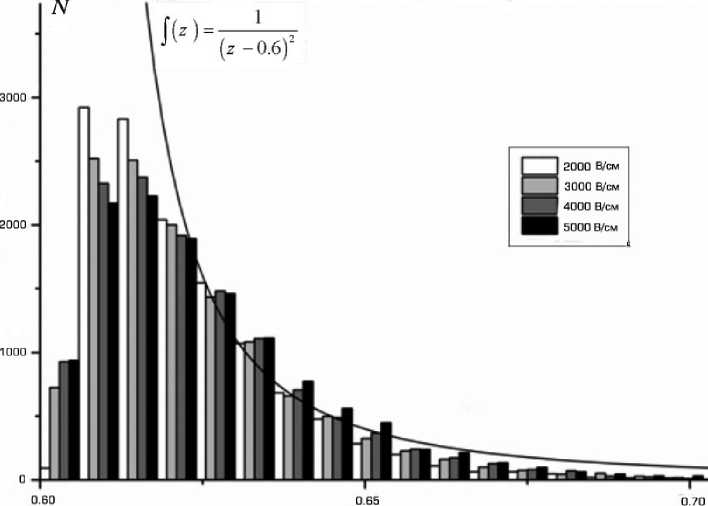
Распределение z -компоненты точки фрагментации для диапазона сильных полей

52. см

e£N ( z 0 ) 7 = 100 эВ. Параметр задачи (5) много больше единицы — 5 = 5 • 10 3 .

Из рисунка видно, что в пределах статистической погрешности вычислительного эксперимента распределения действительно не зависят от величины электрического поля, а "хвост" распределения аппроксимируется обратноквадратичной зависимостью от z -компоненты координаты точки фрагментации в полном соответствии с соотношением (20), из которого следует, что плотность распределения координат точек фрагментации d n / d z ~ V z 2 .

• 2.2.    Однородный газовый поток, однородное электрическое поле

Условия:

N = const, £ = const.          (22)

n = ^{( ц М )} ₁ ^/ 7N A exp L E 0 ) .    (23)

(2nm )¹² 0         ( kT, J

Условие начала фрагментации n >  1 и выражение (23) для n дают следующее значение пороговой величины электрического поля:

_{е а} m+M E 0 N7 /n | < ^M )11 _А1    (2₄)

M e I   [ (2 nm )^1/2 Л ₀

что отличается от элементарной оценки (1) наличием логарифмического члена в знаменателе, учитывающего длину промежутка дрейфа в однородном электрогазодинамическом поле.

ВЫВОДЫ

• 1.    Получены аналитические оценки для критерия начала фрагментации молекулярных ионов при их движении в газовой среде под действием электрического поля. А именно, получены выражения для константы скорости диссоциации, а также для числа фрагментирующих столкновений на заданном промежутке дрейфа в предположении сильного поля, когда распределение ионов по скоростям значительно отличается от максвелловского теплового распределения.

• 2.    Предложенные выражения позволяют оценить величину критического поля, при котором начинается процесс фрагментации в заданной газовой среде и при заданном распределении электрического поля, а также при заданных свойствах иона (масса, сечение столкновений, порог диссоциации).

• 3.    Рассмотрены предельные случаи и получены простые оценки для критерия начала фрагментации в сильных полях для некоторых конфигураций электрогазодинамического поля: однородный газовый поток—однородное электрическое поле и свободно расширяющаяся сверхзвуковая газовая струя—однородное электрическое поле.