О некоторых особенностях формирования напряженно-деформированного состояния в стенке подкрановых балок при движении крана

Сложное напряженное состояние верхней зоны стенки (ВЗС) сварных подкрановых балок формируется крановыми нагрузками через подкрановый рельс и верхний пояс балки. Мостовые краны перемещаются по подкрановому пути с некоторым перекосом и колея крана формируется перед движущемся колесом крана (рис. 1).

При этом крановый рельс смещается, и таким образом возникает эксцентриситет вертикальной нагрузки с учетом пятен контакта на подошве рельса и верхнего пояса. Взаимодействие колеса и рельса – это пример реализации принципа «единства и борьбы противоположностей». Этот принцип всегда проявляется индивидуально, т. е. при изменении направления движения крана и формировании колеи эксцентриситет может менять знак на противоположный.

Рельс всегда стремится к статическому положению на поясе балки, а колесо занимает то пространственное положение по отношению к рельсу,

Рис. 1. Взаимодействие реборды колеса крана с крановым рельсом

которое отвечает минимальному сопротивлению движения колеса и крана. Износ рельса и колеса, показанный на рис. 2, характеризует их взаимную приспособляемость на подкрановом пути, и, как правило, износ головки рельса носит несимметричный односторонний характер (рис. 3).

Рис. 2. Пример износа кранового рельса и колеса крана

Рис. 3. Крановый рельс с односторонним износом головки

Боковой износ головки занимает почти 30 % в общей статистике повреждений рельса [1]. Износ рельса приводит к уменьшению его геометрических характеристик на изгиб ( I x ) и кручение ( I d ), а это в свою очередь увеличивает местные напряжения сжатия (о _1ос ,_у ) и изгиба (о у ,_у ) в ВЗС. Причем износ рельса больше влияет на величину з^_у , так как момент инерции рельса на кручение входит в расчетную формулу без снижения, в то время как момент инерции на изгиб входит в степени 0,3, т. е. (I x )^0.3. Отечественные нормы проектирования [2] не учитывают факт физического износа крановых рельсов при эксплуатации и уменьшения их служебных геометрических характеристик. Европейские нормы [3], напротив, при расчете прочности подкрановых конструкций рекомендуют учитывать физический износ крановых рельсов и приводят предельные нормативы износа для крановых рельсов различного типа.

Крановый рельс в подкрановом пути представляет собой бесконечно длинную балку на уп- ругом основании, нагруженную локальными вертикальными и горизонтальными силами. Локальный изгибающий (крутящий) момент, перпендикулярный продольной оси балки, формируется действием этих сил и рекомендуется определять по формуле [2]:

M t = γ f γ f1 F n e + 0,75 Q t h r ,                   (1)

где е – эксцентриситет приложения вертикальной нагрузки от колеса крана относительно вертикальной оси стенки балки и условно принимаемый равным 0,2 b_r , где b_r – ширина подошвы рельса; Q_t – боковая сила, вызываемая перекосом мостовых кранов при движении и непа-раллельностью крановых путей. Величина боковой силы условно принимается равной Q _t = 0,2 F_n .

Преобразуем формулу (1), используя значения входящих в неё параметрв для проверки статической и усталостной прочности ВЗС для балки с краном режима работы 7К:

– при расчете на статическую прочность

M t = F n h r (0,384 + 0,15);                   (1а)

– при расчете на усталостную прочность

M t = F n h r (0,192 + 0,09).                  (1б)

Из формул (1а) и (1б) видно, какое влияние на величину изгибающего момента оказывает боковая сила (второе слагаемое).

Формула (1) может быть использована только при проверке статической прочности ВСЗ, так как оба слагаемых имеют параметры с некоторой неопределенностью по величине ( е и Q t ), что нерационально, на наш взгляд, для оценки усталостной прочности ВЗС по формуле (173) [2].

В этом случае более достоверные результаты при проверке на выносливость ВЗС может дать использование угла поворота верхнего пояса балки для вычисления местных локальных напряжений σ f _y при поперечном изгибе стенки. Угол поворота интегрально включает в себя и состояние подкрановых путей при движении крана с перекосом, и степень износа крановых рельсов, и состояние креплений рельса к поясу балки, и величину вертикального давления колес крана, и эксцентриситет его приложения. Т. е. угол поворота пояса балки – это интегральная характеристика локального крутящего момента.

Местные напряжения изгиба O f _y в стенке балки, соответствующие максимальному углу поворота полки, могут быть вычислены по формуле [4]:

° f- = ^fc ^Q0 = 2,2 ^Q0 ,         (2)

где t_w и h_w – толщина и высота стенки балки; 6 0 - угол поворота пояса балки.

Экспериментальные исследования В.И. Кам-барова [5] в цехах тяжелого режима работы на сварных подкрановых балках показали, что среднестатистическое значение угла поворота пояса в середине панели d изменяется в широком диапазоне 6 = 0,001^0,007 рад. Корреляционная зависи- мость угла поворота полки от отношения F/I с коэффициентом корреляции γ = 0,92 имеет вид:

0 = 0,1875 ( F / I f ) - 0,00255 (рад). (3)

В формуле (3) F – среднее давление от колес кранов, перемещающихся по балке; I f – суммарный момент инерции рельса и пояса на кручение.

Высокая степень корреляции зависимости (3) свидетельствует о том, что поворот полки происходит в основном за счет давления колеса крана F при эксцентриситете е, равном расстоянию от оси балки до центра тяжести пятна контакта подошвы рельса с поясом. Только незначительная его часть реализуется за счет боковой силы Q t . Это подтверждает высказанную гипотезу о механизме формировании колеи подкранового пути.

Для выяснения механизма формирования угла поворота пояса балки 0 при движении колеса крана с учетом её геометрических размеров и типа рельса рассмотрим крановый рельс как бесконечно длинную балку на упругом основании, загруженную в середине панели d локальным крутящим моментом M t (рис. 4), перпендикулярным к продольной оси балки. В качестве упругого основания принимаем стенку балки, упругие свойства которой характеризует коэффициент податливости при поперечном изгибе (кручении) k_t . Считаем, что при кручении отрыва подошвы рельса от пояса балки не происходит благодаря работе креплений рельса. Из этой предпосылки следует, что угол поворота рельса совпадает с углом поворота пояса балки.

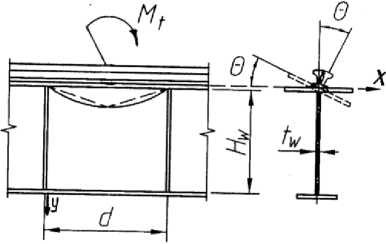
Рис. 4. Расчетная схема ВЗС и рельса на кручение

Согласно [6], дифференциальное уравнение кручения балки на упругом основании имеет вид:

EI ф 0^ - GI d 0^ ) = m ₍ х ) ,

где EI _φ и GI_d – жесткость рельса соответственно при стесненном и свободном кручении; 0 (_Х ) - угол поворота рельса; m ( _x ) – реактивный момент упругого основания, который можно представить в виде

m ( х ) = - k t 0 (_Х )                                     (5)

Подставив (5) в (4) и выполнив некоторые преобразования, получим дифференциальное уравнение в виде

9^ ) - 2 r ² 9 (Х) + 5 ⁴ 9 ( х ) = 0, (6) где r ² = GI d / EI φ ; s ⁴ = k t / EI φ . (7)

Решение уравнения (6) будем искать в виде

9 ( х) = е ^ах ,                                          (8)

где α – неизвестный множитель, который необходимо определить.

При заданной функции угла поворота (8) дифференциальное уравнение (6) примет вид:

а4 еах - 2 r2 а2 еах + 54 еах = 0.(9)

Сократив на общий множитель е ^ах уравнение (9), получим характеристическое уравнение для определения множителя α :

а4 - 2 r2 а2 + 54 = 0.(10)

Корни биквадратного уравнения (10) вычисляются по формулам (11) и зависят от соотношения параметров s и r :

ах_4 = ± Jr2 ±/г4 ± s4 .

Выполним анализ фактических соотношений между параметрами s и r. Из выражений (7) следует, что параметра r² определяется отношением геометрических характеристик крановых рельсов при кручении. Приняв во внимание, что G = E / 2(1 + ц ) и коэффициент Пуассона μ = 0,3, получим:

г² = ^/41 ф (1+р) = 0192 I_d/ 1 ф .           (12)

Воспользовавшись значениями I d и 1_ф из [7], определим параметр r для крановых рельсов, используемых в подкрановых путях (табл. 1).

Таблица 1

Значения параметра r для крановых рельсов

Рельс	КР70	КР80	КР100	КР120	КР140
т      4 Id , cм4	253	387	765	1310	2130
I φ , см6	14100	26400	76400	191000	384000
I d / Iφ	0,018	0,015	0,010	0,007	0,006
_ -1 r , см–	0,059	0,053	0,044	0,036	0,033

Параметр s ⁴ (см. (7)) зависит от коэффициента податливости упругого основания при кручении k_t . Используя (5), выразим k_t в виде:

k t =  - ^ (х)^{/ 9} (х) .

Угол поворота пояса балки 9 _(Х) , согласно [4], при действии сосредоточенного крутящего момента М t , приложенного в середине панели балки, равен:

М         _e j(x-0.5d) __e -T(x+0.5d)

^(x)    2 р [             y (1+e^{- Y d} )

где γ = ( p / q )^0,5;

p =       + 2(1-ц) Dfbf + g Id;(15)

q =      + d_^ + e(16)

q     105       12

В формулах (15)-(16) D w =     Е ‘^w 2 и

^{12 (1-} H )

Df =    Е^{t f} 2

f 12 (1- h ²)

– цилиндрическая жесткость стенки и полки соответственно; hw – высота стенки балки;

t w – толщина стенки; b f – ширина верхней полки; t f – толщина верхней полки; d – длина панели.

Расчеты по формулам (14)–(16) типовых подкрановых балок показали, что доля стенки балки в восприятии локального крутящего момента составляет от 0,8 до 7,2 % крутильной жесткости верхней зоны балки, т. е. стенка практически не сопротивляется повороту пояса в середине панели. Локальный крутящий момент воспринимается исключительно за счет крутильной жесткости кранового рельса и пояса, доля которого составляет всего 6–15 %, т. е. в формировании угла поворота пояса основную роль играет крановый рельс и его крепления к поясу.

Реактивный момент m (X) распределяется по длине панели балки d по криволинейной эпюре, совпадающей с законом изменения местных из-гибных напряжений. Для упрощения расчетов принимаем вместо криволинейной эпюры изменения m ( _X ) треугольную эпюру (см. рис. 4). Эта предпосылка дает возможность записать, что 0,5 ·m ( _X ) · d = М_t , откуда

m ( Х ) = 2 M t / d . (17)

Подставив значения (14) и (17) в (13), получим выражение для вычисления коэффициента упругой податливости стенки подкрановой балки при местном кручении:

k t =

4 рГ        у (1+ е ^-yd)        "

d [х-у (1+ е ^-y^d )- ( е ^-У^(х+0^У) _

Из (18) следует, что при x = 0 и x = d k_t →∞, а при x = 0,5 d (середина панели) коэффициент податливости при кручении имеет минимальное значение.

kt

4-р Г        у(1+e-Yd)        1    8^р d [o,5d^y(1+e-Yd)—(1—e-Yd)]    d2 *

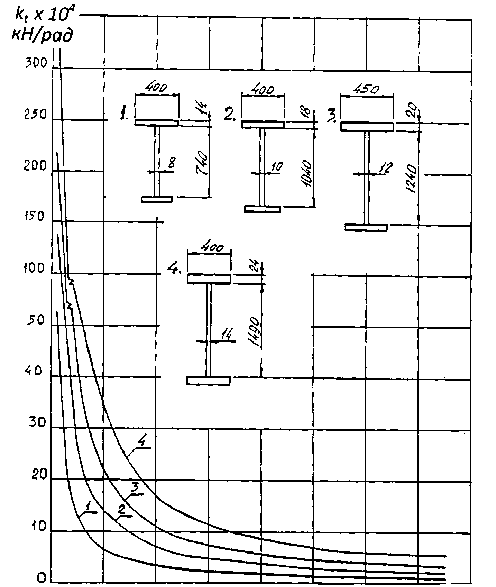
Это подтверждается расчетом подкрановых балок разного поперечного сечения с длиной панели d = 1,5 м и рельсом КР 70. Результаты расчета представлены в табл. 2 и на рис. 5.

Зависимости, представленные на рис. 5, показывают, что максимальный угол поворота пояса и наибольшие изгибные напряжения будут в середине панели d .

Таблица 2

К расчету коэффициента k t для подкрановых балок

№ балки на рис. 5	Характеристики балок
	D w · 104, кН · см	D f · 104, кН · см	G I d · 104, кН · см2	E I φ · 104, кН · см4	p · 104, кН · см2	q · 104, кН · см4	γ, см–1
1	0,0961	0,515	КР 70 199,5	КР 70 28905,0	230,2	32023,0	0,085
2	0,188	1,095			266,0	36756,0	0,085
3	0,324	1,054			304,8	41194,0	0,081
4	0,515	2,595			365,3	58969,0	0,079

16    20    ?0    40 JO 60     70 d, CM

Рис. 5. Изменение коэффициента податливости стенки балки при действии местного крутящего момента

На рис. 6 представлена зависимость коэффициента k t , min , т. е. в середине панели d от её длины. Из рис. 6 следует, что с увеличением длины панели стенки d коэффициент податливости стенки на кручение уменьшается. Поэтому учитывать в расчетах жесткостные характеристики стенки балки рационально только при расстоянии между ребрами жесткости не более 2 метров.

С учетом выражения (19) параметр s4 примет вид:

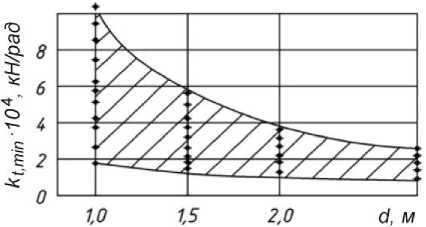
Рис. 6. Зависимость минимального значения коэффициента k t от длины панели d

s4 _   8-Р d 2 -Ely

Расчеты по формуле (20) сварных подкрановых балок пролетом 6 и 12 м под краны грузоподъёмностью не более 500 кН показали, что параметр s изменяется диапазоне s = 0,041…0,047. В практических расчетах можно использовать среднее значение s = 0,044.

Для большинства сварных подкрановых балок, эксплуатируемых с крановыми рельсами КР 70 – КР 100, r >  s , что позволит вычислить корни биквадратного уравнения (7):

a1 = Jr2 + Vr4 — s4; a2 = —Vr2 + Vr4 — s4

<       \------ (21)

a3 = Jr2 — Vr4 — s4; a4 = —^2 — Vr4 — s4

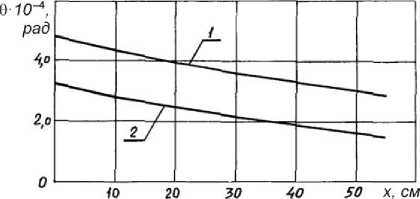
Рис. 7. Распределение угла поворота 9 по длине панели d рельса КР 80 при действии M t = 10 кН·м: 1 – рельс на балке l = 6 м ( k t = 9,7·10⁴ кН/рад);

2 – рельс на балке l = 12 м ( k t = 21,2·10⁴ кН/рад)

Зная корни характеристического уравнения, можно записать решение однородного дифференциального уравнения (8) в виде:

9(х) = C1 • eaiх + C2 • e—a2х + C3 -е“зх +

+C4 • e—a4X,

где С 1 , С 2 , С 3 , С 4 – постоянные интегрирования, определяемые из граничных условий:

при x = 0 θ ( x ) = 0; х → ∞ θ ( x ) = 0.        (23)

Следовательно, постоянные интегрирования С ₂ и С ₄ в выражении (22) обращаются в нуль благодаря множителю e^—ax, а два других слагаемых обращаются в нуль лишь при С ₁ = С ₃ = 0. Постоянные интегрирования С 2 и С 4 найдем из граничных условий (а).

C 2

М t 2EIya i [a² —a²]

, C 4

М t 2EIy -a 3 [a²—a²]

Подставив (24) в (22), получим выражения для вычисления угла поворота θ ( x ).

Угол поворота:

⁹ ( х )

M _t       / e^—a 1 ^х e^—a 3 ^х

2EIy[a² —a²]    a i        a g

С использованием выражения (25) вычислены значения угла поворота рельса КР80 и верхнего пояса балок пролетом 6 и 12 м при действии сосредоточенного момента М_t = 10 кН·м. Из эпюр, представленных на рис. 7, следует, что угол поворота распределяется на расстояние большее, чем длина панели, т. е. рельс за счет неразрезности передает часть локального крутящего момента на соседние панели стенки.

Заключение

Учет совместной работы рельса и пояса подкрановой балки позволяет приблизить расчетную модель к фактической работе рельса в подкрановых путях производственных зданий. Расчеты показали, что величина локальных напряжений от кручения ВЗС с использованием угла поворота пояса меньше, чем по методике СП в 2,0–2,8 раза. Это вызвано тем, что экспериментальные углы поворота пояса действительно отражают фактическую нагруженность ВЗС балок и отмеченные выше факторы, а в расчетной модели принята совместная работа рельса и пояса. Однако реализовать такую расчетную модель в производстве невозможно из-за отсутствия как креплений рельсов, так и рельсов с нужной геометрией подошвы. Стандартные крепления прижимными планками не отвечают условиям эксплуатации при режимах работы кранов 7К и 8К.

Кардинально решить вопрос об усталостной прочности ВЗС сварных подкрановых балок можно только при использовании под подошвой рельса низкомодульных прокладок [8–10] или применяя сварные балки с верхним поясом из широкополочных тавров [11].