О некоторых особенностях определения качества продукции на примере данных одного из ведущих отечественных автопроизводителей

EDN: PSUWIX

Экспоненциальный характер распределения вероятностей безотказной работ. В анализе данных эмпирические частоты тех или иных событий получаются непосредственно из датафрейма путём подсчёта частот соответствующих записей. Однако интересен вопрос, можно ли аппроксимировать эмпирическое распределение при помощи какой-либо теоретической функции. В этом разделе ключевой характеристикой служит пробег автомобиля, а ключевая задача — описать распределение вероятностей обнаружения дефектов в зависимости от пробега.

Характеристики выборки. Датафрейм содержит 65 534 записей о дефектах автомобилей, обнаруженных в первого года эксплуатации автомобилей года. Объектами датафрейма служат обращения владельцев в сервисные центры, признаки описывают различные характеристики обращения. Каждый объект описывается при помощи 22 признаков, из которых для решения нашей задачи нам понадобятся только два: id — уникальный идентификатор изделия, и distance — пробег автомобиля на момент обращения в сервисный центр.

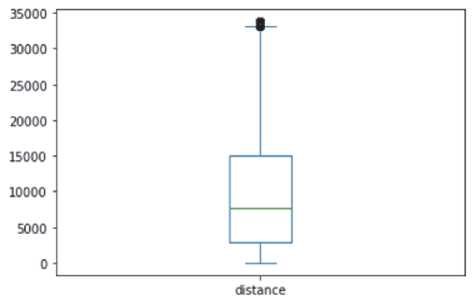
Подавление выбросов (рисунок 1). Максимальная величина пробега в исходной выборке — 91 124. Используя процентиль на уровне 99.5, обнаруживаем, что 99.5% всех пробегов не превосходят 33 815. Нетипичные величины пробега могут привести к искажениям, поэтому мы проводим локализацию датафрейма на типичные пробеги, удаляя все записи, пробеги

которых превосходят 33 815. При этом удаляется только 0.5% всех записей, после чего в датаф-рейме остаётся 65 204 объектов.

Эмпирические вероятности. Обозначим DF множество всех записей датафрейма, D — множество всех значений признака distance, n — объем выборки, k — число интервалов, на которые разбивается D . Шаг разбиения вычисляется:

, max (d)— min (D)

/1 = -----------—.        (1)

к

Пусть m_i — объем локализации, в который попадают первые i шагов разбиения. Тогда эмпирические вероятности того, что на пробеге min(D) + (i + l)/i было совершено хотя бы одно обращение в сервисный центр вычисляются так:

Pi =

n —m:

Используя идентификатор изделия, выделяем из общего массива обращений DF записи, соответствующие первым обращениям, до которых изделие работало безотказно. Получаем датафрейм DFioc объёмом 23 901, для которого получаем ещё одну серию эмпирических вероятностей (рисунок 2).

Теоретическое распределение вероятностей. Безотказная работа подчиняется однопараметрическому экспоненциальному распределению с плотностью

f(x) = ae “^x. (3)

Однако, поскольку горизонтальная координата имеет порядок 10 ⁴ , мы ее масштабируем

f(x) = ae ^ах’,гдех = —--^      . (4)

max(o)-min(D)

Вводим ещё один параметр 5 для тонкой настройки коэффициента масштабирования:

О о о

dstance

а) Выборка до подавления

b) Выборка после подавления

Рисунок 1 – Подавление выбросов

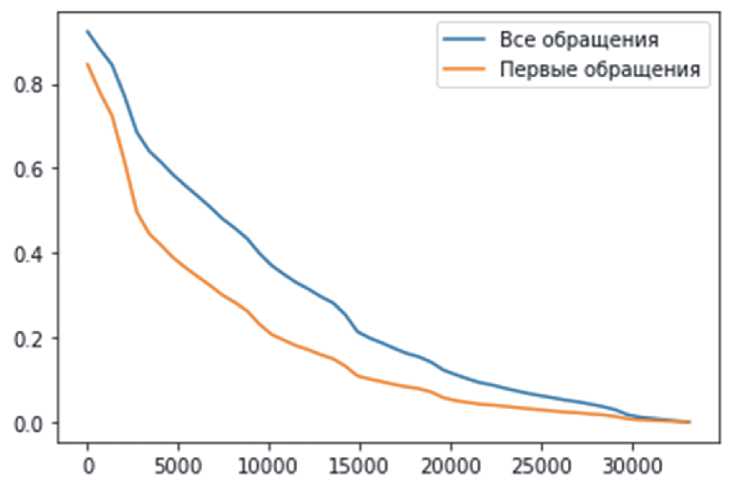
Рисунок 2 – Распределения вероятностей a) всех случаев обращения и b) первых случаев обращения в сервисные центры, отнесенные к пробегу (км). Здесь и везде далее k = 50

а ,

.

Таким образом, получается двухпараметрическое экспоненциальное распределение. Наша дальнейшая задача состоит в подборе таких значений параметров и , что при их подстановке в формулу для теоретические распределения будут наиболее точно приближать полученные выше эмпирические распределения.

Сеточный метод подбора параметров. Будем подбирать параметры и , исходя из минимизации среднеквадратичной ошибки :

<7 = -Z^oCfUt) - Pi)2 -» min ,

. (6)

Для этого используем серию последовательных приближений. Сначала зададим рандомно промежутки для изменения и и с грубым шагом пройдём по двумерной сетке, в каждом узле которой построим массив и сравним его с массивом в смысле заявленной выше оценки. Затем выберем узел с наименьшей ошибкой и в его окрестности снова зададим двумерную сетку с более мелким шагом. И так далее до тех пор, пока среднеквадратичная ошибка не перестанет уменьшаться.

Подбор параметров теоретического распределения для случая всех обращений.

Проход 1. Параметры:,

, шаг сетки:           . Оптимальные значения параметров,

, при этом ошибка.

Проход 2. Локализуем значения параметров в окрестности значений, найденных на предыдущем этапе. Параметры:,

, шаг сетки:             . Оп-

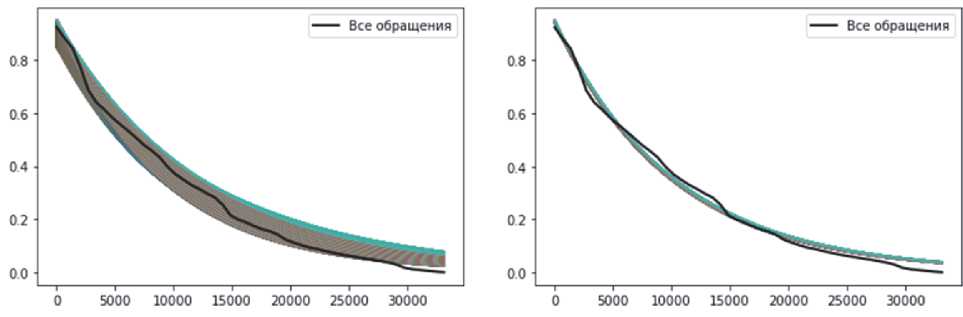
а) Грубый шаг сетки (второй проход)            b) Тонкий шаг сетки (третий проход)

Рисунок 3 – Сеточный метод последовательных приближений.

Вероятности безотказной работы (ось y), отнесенные к эксплуатационному пробегу (ось x), км

тимальные значения параметров           ,

, при этом ошибка               .

Ошибка уменьшилась.

Проход 3. Локализуем значения параметров в окрестности значений, найденных на предыдущем этапе. Параметры:

,                   , шаг сетки:            . Оптимальные значения параметров           ,

, при этом ошибка              .

Ошибка перестала уменьшаться, выходим из процедуры.

Таким образом, теоретическая плотность распределения вероятностей для случая всех обраще- ний в сервисные центры имеет следующий вид:

.

Подбор параметров теоретического распределения для случая первых обращений. Аналогично поступаем с датафреймом , составленным из первых обращений.

Проход 1. Параметры:,

, шаг сетки:         . Оптимальные значения параметров         ,, при этом ошибка.

Проход 2. Локализуем значения параметров в окрестности значений, найденных на предыдущем этапе. Параметры:,

, шаг сетки:            . Оптимальные значения параметров,

, при этом ошибка.

Ошибка уменьшилась.

Проход 3. Локализуем значения параметров в окрестности значений, найденных на предыдущем этапе. Параметры:,

, шаг сетки:            . Оптимальные значения параметров,

, при этом ошибка.

Ошибка перестала уменьшаться, выходим из процедуры.

Таким образом, теоретическая плотность распределения вероятностей для случая всех обращений в сервисные центры имеет следующий вид:

.                 (8)

Сравнивая среднеквадратичные ошибки для двух полученных теоретических плотностей, замечаем, что в случае первых обращений она ниже. Это вполне согласуется с общей теорией вероятностей, так как экспоненциальное распределение описывает именно отрезок до первого наступления какого-либо события, в нашем случае – до первого обращения в сервисный центр. Экспоненциальный характер плотности распределения вероятностей всех обращений является менее выраженным.

Время, затраченное на гарантийное обслуживание в течение первого года эксплуатации, как показатель качества продукта. Говорить, что основным (или даже единственным) показателем качества продукта является его надёжность, вполне допустимо, и об неоднократно писали многие авторы. Но в современных условиях производства и потребления такая точка зрения становится все более архаичной. Примем в качестве постулата, что качество продукта определяет не производитель, а потребитель. Мы не можем провести опрос среди потребителей, у нас нет таких возможностей. Но, если отталкиваться от имеющихся у нас данных, мы можем вычислить среднее время, которое тратит потребитель на гарантийное обслуживание изделия в течение первого года его эксплуатации. Косвенно это время характеризует надёжность продукта (чем оно меньше, тем надёжнее продукт), но самое главное — оно оценивает удовлетворённость потребителя: чем меньше время, в течение которого изделие вынужденно не эксплуатируется, тем лучше для потребителя, тем качественнее, с его точки зрения, оказывается продукт.

Итак, с большими оговорками и только в пределах этой работы под качеством мы бу- дем понимать определённое выше время. Кроме того, мы будем считать, что продукт — не конкретное изделие, а совокупность сразу нескольких систем: a) производства, b) сервисной инфраструктуры, c) логистики этой инфраструктуры и даже d) её юридической базы.

Характеристики выборки. Датафрейм содержит 1 230 475 записей о дефектах автомобилей, обнаруженных в течение двух лет эксплуатации автомобилей. Объектами датафрейма служат обращения владельцев в сервисные центры, признаки описывают различные характеристики обращения. Каждый объект описывается при помощи 22 признаков. Для решения задачи будем использовать следующие признаки:

product_id — уникальный идетнификатор изделия, sale — дата продажи изделия в формате YYYY-MM, date_in — дата обращение в сервисный центр для устранения дефекта по гарантийному соглашению в формате YYYY-MM-DD, date_out — дата устранения дефекта в формате YYYY-MM-DD, cities — название города, в котором расположен сервисный центр, model — номер модели конкретного изделия.

Кроме того сгенерируем дополнительный признак, характеризующий разность между временем поступления изделия в сервисный центр и временем полного выполнения всех работ по устранению дефекта (или нескольких дефектов):

diff_days — время в днях, потраченное потребителем на устранение дефекта, получается как разность date_out – date_in.

Псевдокод алгоритма

Шаг 1. Определяем пустой список T_list. В этот список мы будем заносить среднее время, которое потратили пользователи продукта на гарантийное обслуживание в течение первого года эксплуатации.

Шаг 2. Присваиваем счётчику месяца стартовое значение.

Шаг 3. Производим локализацию исходного датафрейма df до датафрейма df_year_month по следующим условиям: a) год продажи, b) месяц продажи равен счётчику, c) год обращения не превосходит следующий после продажи год, d) месяц обращения равен счётчику.

Шаг 4. Выделяем все уникальные идентификаторы из получившейся локализации df_year_ month в виде списка product. Так получаются все изделия выпущенные в указанном месяце в анализируемом году.

Шаг 5. Формируем пустой датафрейм DF с двумя признаками: a) идентификатор изделия и b) суммарное время, потраченное пользователем на гарантийное обслуживание в течение первого года эксплуатации.

Шаг 6. Присваиваем счётчику изделия стартовое значение.

Шаг 6.1. Проводим локализацию датафрей-ма df_year_month до датафреймаdf_loc по условию: идентификатор изделия равен текущему значению из списка product,

Шаг 6. 2. Заносим в датафрейм df_loc строку с текущим значением идентификатора и суммой элементов второго столбца.

Шаг 7. Повторяем шаг 6 до исчерпания списка product.

Шаг 8. Добавляем в список T_list среднее значение второго столбца датафрейма DF.

Шаг 9. Увеличиваем счётчик месяцев на 1.

Шаг 10. Повторяем, начиная с шага 3, до тех пор, пока счётчик месяцев не примет значение 12.

Таким образом, возникает список из 12 значений T_list. Первый элемент: пользователи, купившие изделие в январе первого исследуемого года, а в течение первого года эксплуатации в среднем затратили столько времени (в днях) на гарантийное обслуживание. Второй элемент: пользователи, купившие изделие в феврале в течение первого года эксплуатации в среднем затратили столько времени (в днях) на гарантийное обслуживание. И так далее.

Сравнение качества по категориям. Если локализовать датафрейм df_year_month дополнительно по ещё одному признаку, то можно сравнивать качество продукта в какой-либо отдельной категории (например, по городам или по моделям).

Сравнение по городам (рисунок 4). Добавим в пункт 3 алгоритма ещё одну дополнительную локализацию: e) значение cities равно названию конкретного города, и реализуем алгоритм дважды — для Самары и для Москвы. В результате получим два списка: T_list_Samara и T_list_ Moscow.

Мы видим, что пользователи, купившие изделие в январе года и обслуживавшие его в Самаре, потратили за первый год эксплуатации 3.9285 дня на гарантийное обслуживание, в то же время, при обслуживании в Москве на это уходило 0.8641 дня, то есть — в разы меньше. И так далее по месяцам покупки. В чем причина столь значительных различий — открытый вопрос, требующий дополнительных исследований. Возможно, все дело в логистике, которая в Москве лучше, чем в Самаре, и запчасти в сервисы поставляются гораздо быстрее. Возможно, дело не в этом, а в чем-то другом. Но, так или иначе, разница в качестве продукта налицо. Подчеркнем еще раз, что под продуктом мы понимаем не отдельно взятое изделие, а целую совокупность различных систем, в частности — сервисное обслуживание.

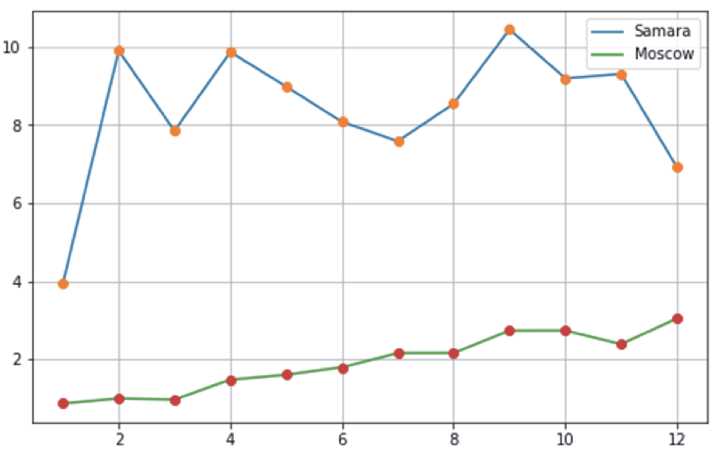
Рисунок 4 – Сравнение по городам.

Количество дней, затраченных на обслуживание автомобилей (ось Y), отнесенные к месяцу года (ось X)

Сравнение по моделям (рисунок 5). Аналогично, выполняя дополнительную локализацию по двум моделям, получим два списка: T_ list_21140 и T_list_21074.

Здесь преимущество не столь ярко выражено, но, тем не менее, оно очевидно: модель 21074 является более качественной по сравнению с моделью 21140. Видимо, при сравнении по моделям выигрыш одной из них получается за счёт конструктивных решений. Хотя, возможно, все дело опять в логистике: просто запчастей для выигрышей модели больше, и сервисы не испытывают дефицита. А может быть, работает комплекс причин.

Другие категории. Можно сравнивать и другие категории, например, отдельные сервисные центры в пределах одного города, отдельные сервисные центры разных городов, и т. д.

Рейтинги качества по категориям. Если усреднить введённый нами показатель по году, то получится, что каждый элемент категории (город, модель и т. д.) описывается не списком из 12-то позиций, а одним числом. Тогда все элементы категории упорядочиваются по этому числу и возникает рейтинг элементов категории.

Рейтинг по городам

Например, так выглядит рейтинг по городам, в которых представлены сервисные центры (таблица 1).

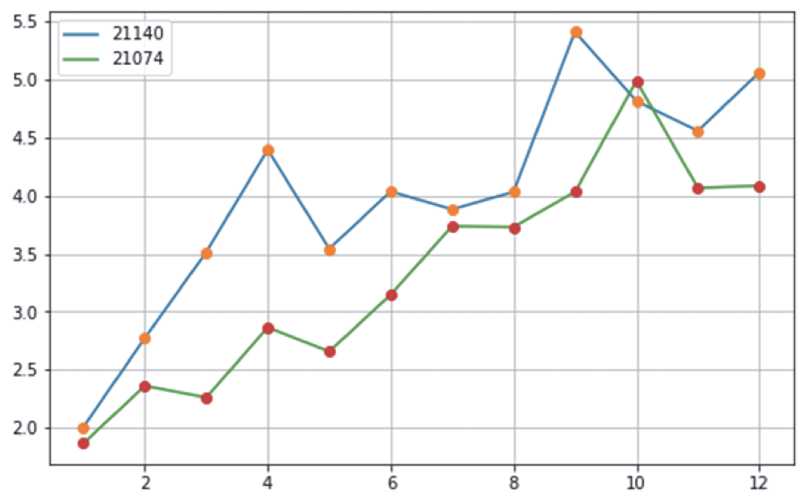
Рисунок 5 – Сравнение по моделям.

Количество дней, затраченных на обслуживание автомобилей (ось Y),

отнесенные к месяцу года (ось X)

Таблица 1 – Рейтинг по городам

	cities	times			cities	times
1	Yakhroma	0.006944		42	Surgut	1.405442
2	Elista	0.008621		43	Naberezhnye Chelny	1.426851
3	Salsk	0.011111		44	Ukhta	1.458390
4	Irkutsk	0.020125		45	Shadrinsk	1.471642
5	Syzran	0.022975		46	Ufa	1.659502
6	Tula	0.034136		47	Moscow	1.906411
7	Kirov	0.044102		48	Krasnodar	1.949471
8	Kulakov	0.059942		49	Ivanovo	2.203782
9	Syktyvkar	0.093531		50	Chelyabinsk	2.301574
10	Chita	0.132246		51	Ryazan	2.326658
11	Tomsk	0.132438		52	Tambov	2.345489
12	Bryansk	0.135313		53	Novocheboksarsk	2.524652
13	Oryol	0.159401		54	Novosibirsk	2.579909
14	Vladimir	0.160241		55	Chekhov	2.948030
15	Tver	0.161153		56	Volgograd	3.245606
16	Tyumen	0.179465		57	Sochi	3.254884
17	Ulan-Ude	0.180556		58	Kazan	3.595801
18	Blagoveshchensk	0.185419		59	Engels	3.629520
19	Veliky Novgorod	0.232429		60	Omsk	3.936059
20	Kostroma	0.282750		61	Izhevsk	4.080257
21	Vladikavkaz	0.319444		62	Krasnoyarsk	4.403866
22	Nizhnekamsk	0.389729		63	Stary Oskol	4.496346
23	Kuznetsk	0.462068		64	Vologda	4.778492
24	Kaspiysk	0.498859		65	Yekaterinburg	5.061532
25	Barnaul	0.527353		66	Petrozavodsk	5.362451
26	Ulyanovsk	0.652053		67	Severodvinsk	5.656526
27	Taganrog	0.692261		68	Belgorod	5.994623
28	Kursk	0.757976		69	Voronezh	6.826864
29	Yaroslavl	0.886420		70	Armavir	7.250200
30	Penza	0.956379		71	Saint Petersburg	7.465268
31	Maykop	0.963014		72	Samara	8.382268
32	Astrakhan	0.966997		73	Tolyatti	8.885434
33	Saransk	0.997983		74	Nizhny Novgorod	8.941720
34	Rostov-on-Don	1.087247		75	Kaluga	10.432756

Таблица 1 – Рейтинг по городам (окончание)

35	Arkhangelsk	1.149043		76	Smolensk	10.668645
36	Sarov	1.187686		77	Yoshkar-Ola	11.939166
37	Yuzhnouralsk	1.221315		78	Voskresensk	13.428175
38	Timofeevka	1.257528		79	Novokuznetsk	14.715561
39	Stavropol	1.269960		80	Lipetsk	14.750209
40	Lermontov	1.356052		81	Orenburg	18.630320
41	Perm	1.397743		82	Orsk	18.889513

Таблица 2 – Рейтинг по моделям

	models	times			models	times
1	21114	3.256550		8	21101	4.055908
2	21053	3.261485		9	21124	4.325127
3	21074	3.315351		10	21121	4.358504
4	21150	3.341051		11	21104	4.928510
5	21112	3.342298		12	21310	5.039310
6	21130	3.834625		13	21214	5.414846
7	21140	4.002050		14	11183	5.773512

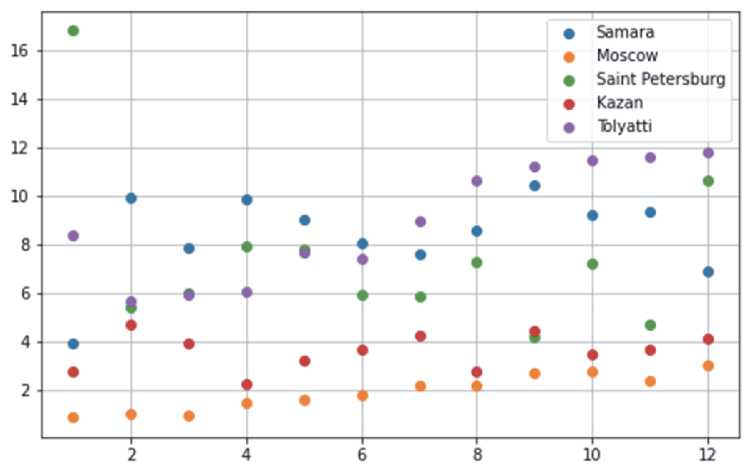
Рисунок 6 – Динамический рейтинг по городам.

Количество дней, затраченных на обслуживание автомобилей (ось Y), отнесенные к месяцу года (ось X)

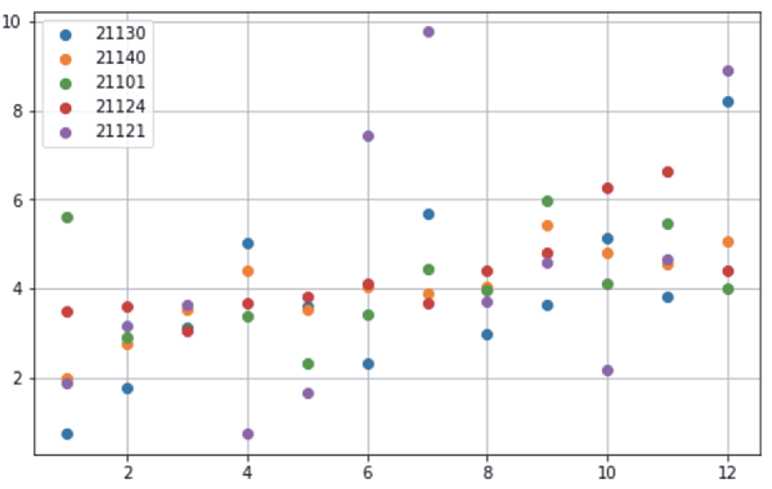
Рисунок 7 – Динамический рейтинг по моделям.

Количество дней затраченных на обслуживание автомобилей (ось Y), отнесенные к месяцу года (ось X)