О некоторых особенностях структурирования металлических жидкостей

Исследования структуры жидкостей Дебаем и Шеррером с помощью рассеяния рентгеновских лучей впервые показали, что расположение частиц в жидкости не беспорядочно и имеет сходство с их расположением в кристалле. Это принципиально отличало их результат от геометрического подхода Дж. Бернала.

Физическое обоснование рентгеноструктурных данных предложено Я.И. Френкелем [1], а дальнейшее их развитие принадлежит Эйрингу [2]. Так появилась теория дырочного строения в виде квазирешетки с частично вакантными узлами.

Однако еще в 1931 году Стюарт представил на обсуждение модель строения жидкости в виде связанных между собой сиботаксисов, в которых после плавления кристалла сохраняется упорядочение частиц. Сиботаксисы неустойчивы и характеризуются высокой динамичностью: разрушаясь в одном месте, они возникают в другом. Продолжительность их существования, а также соотношение объемов разупорядоченной и упорядоченной частей жидкости определяются параметрами состояния системы [3]. Основные положения модели нашли применение при разработке таких многоатомных ансамблей, как микрогруппировки, рои, кластеры и т. д.

Прошли годы и, благодаря активным исследованиям строения и свойств жидких металлов и сплавов различными научными школами, можно считать установленным, что металлические жидкости по своей структуре являются микронеоднородными и неравновесными [4, 5]. Как следствие, эти особенности структуры расплава оказывают влияние на эффективность технологических процессов и формирование качественных показателей металлопродукции [6, 7].

Согласно представлениям, сложившимся в физике металлических жидкостей, тепловое движение атомов в основном составляет их колебательное (волновое) движение вокруг положения равновесия с постоянной частотой ћ с /λ, где λ – длина волны колебательного движения, с – скорость света и ћ – постоянная планка к периодам колебаний 10^–14–10^–18 с. Квант энергии теплового колебательного движения атомов назван фононом. Время его жизни 10^–11 с, что на 2–3 порядка превышает продолжительность колебаний одиноких атомов. При нагреве до температуры Дебая количество фононов определяется как N ф ~ Т ³, а выше температуры Дебая N ф ~ Т [8].

Плотное расположение атомов в жидкости способствует тому, что любое колебательное движение произвольно выбранного атома может происходить только в том случае, если соседствующий с ним атом в своем колебательном движении будет двигаться в том же направлении. Область жидкости, в пределах которой тепловые колебания атомов согласованы – это кластер. Размеры таких микрообластей превышают несколько координационных сфер. От центра кластера к периферии степень атомной упорядоченности уменьшается, что обеспечивает плавное структурное сопряжение с разупорядоченной зоной.

Под влиянием флуктуаций тепловой энергии в одних микрообъемах жидкости кластеры распадаются, а в других – зарождаются. Локальная неустойчивость кластеров характеризуется средней продолжительностью их жизни τ_кл ≥ 10 ^{- 9} с, тогда как среднее время жизни термодинамических флуктуаций плотности, по мнению Ашкрофта [9], составляет 10^–13 с, а по данным работы [10] τ_фл = 10^–15–10^–14 с. Приведенные значения τ _кл и τ_фл хорошо согласуются с размерами обсуждаемых микрообъемов. Флуктуации плотности не превышают двух координационных сфер, а кластеры, по мнению многих авторов, обладают значительно большими размерами R _кл ≥ ( 10…25 ) ⋅ 10^–10 м.

Действительно, образование таких больших областей упорядочения в расплавах с упаковкой частиц, близкой к кристаллической, трудно объяснить с позиций флуктуа- ции плотности в жидких металлах, имеющих ту же частоту, что и тепловые осцилляции атомов [9].

При повышении температуры расплава объем и размеры кластеров уменьшаются. Интенсивность этого процесса определяется химическим составом кластера, т. е. зависит от энергии межатомного взаимодействия и внешних воздействий.

Разупорядоченная зона представляет собой непрерывную трехмерную ячеистую структурную составляющую жидкости, заполняющую промежутки между кластерами. Атомы этой зоны колеблются практически независимо от окружения, т. е. переход атома в разупорядоченную зону можно рассматривать как результат исчезновения (испускания) фонона.

Таким образом, состояние жидкости может быть описано в физических терминах, если известны: долевое соотношение ее составляющих, количество, состав и размеры кластеров, число атомов, входящих в кластеры, время жизни кластеров, длина свободного пробега электронов и т. д.

Поэтому в дальнейшем остановимся на тех возможностях количественного описания структурных параметров, которые вытекают из анализа известных публикаций и наших предложений по их использованию. Отметим лишь, что наибольшее внимание в нашем описании уделено не феноменологическим теориям, а работам, в которых предлагаемые на обсуждение модельные представления опираются на результаты экспериментальных исследований.

С целью изучения температурных и концентрационных зависимостей, как правило, используются методики анализа теплопроводности, магнитной восприимчивости, кинематической вязкости, поверхностного натяжения, термо-э.д.с., плотности, отличающихся высокой чувствительностью к структурным изменениям при плавлении и дальнейшем нагреве. Наиболее обоснованными выводами о структурных превращениях и изменениях характера химических связей являются те, которые вытекают из результатов комплексных исследований свойств на одном и том же объекте, а также из результатов рентгеноструктурных, нейтронографических и других прямых методов.

Детальное описание и количественная оценка структурной и химической микроне- однородности жидкостей является задачей многих исследований. В частности, В.И. Архаровым и И.А. Новохатским предложена квазикристаллическая модель строения расплавов [11, 12]. Для количественного описания микронеоднородности авторы ввели характеристику (v), выражающую относитель-

ные доли отдельных структурных составляющих жидкой фазы. В случае многокомпонентной (поликластерной) жидкой фазы эти

доли связаны уравнением вида

К^ кл ) i + ^v раз ^_ 1,

где у кл и V _раз — относительные (атомные или мольные) доли кластеров разных типов и общей разупорядоченной зоны соответственно [13].

Величины у кл и V pai зависят от природы

жидкости и температуры. При достижении жидкостью равновесной для данной температуры структуры между всеми ее составляю-

щими устанавливается состояние динамиче-

ского равновесия.

С ростом температуры равновесное значение относительной доли кластеров уменьшается. При определенной (для каждого типа кластера) температуре ( t раз ) соответствующие

кластеры вырождаются.

Температурная зависимость

У раз имеет

вид [12]

У раз

= А ■ ехр

I

R ■ То)

,

где А - постоянная; А Н ра_з - тепловой эффект процесса термического разупорядочения 1 моля кластеров по схеме

( Ме ) кл = ( Ме ) раз + А Н раз . (3)

Из анализа выражений (1)–(3) следует, что для полного количественного описания структурной микронеоднородности однокомпонентной жидкости необходимо определить тем или иным способом у _раз при какой-либо температуре и А Н ра_з .

Относительную долю разупорядоченной зоны при температуре плавления рассчитывают с привлечением справочных термодинамических данных [14].

Используя зависимость (2) по значениям ( у _раз ) пл и А Н _раз , оценивают температуру полного разупорядочения и относительные

доли структурных составляющих жидкости при различных температурах.

Другие методы расчетов описаны в работах [15, 16] и основываются на первом следствии модели об аддитивности распределения свойств жидкости Ф у по ее структурным составляющим.

Для однокомпонентной жидкости при всех t <  t _раз следует

^Ф У ^{_ ф}_ю ■V _Kn ⁺ Ф раз ■ У раз ,              ⁽⁴⁾

где Фкл , Фраз – парциальные значения какого-либо свойства для кластеров и разупорядо-ченной зоны.

Температура полного разупорядочения жидкого металла разделяет две различные области температурной зависимости и свойства Ф^ . В области t > tраз последняя представляет собой температурную зависимость парциального свойства для разупорядоченной зоны. Экстраполяцией в область t < tраз рассчитывают все значения Ф и для более раз низких температур.

Таким образом, для развития количественной теории квазиполикристаллической модели необходимы экспериментальные методы определения относительных долей структурных составляющих расплавов: раз-упорядоченной зоны и зоны кластеров. Можно полагать, что именно этими характеристиками определяются многие структурночувствительные свойства расплавов и процессы, связанные с изменением их структуры [16–19].

Принципиальные основы разработанного экстраполяционного термодинамического метода определения в расплавах относительных долей кластеров и разупорядоченной зоны в широком интервале температур хорошо описаны в работе [4]. Метод основан на допущении, что при больших перегревах расплавов кластеры полностью исчезают, т. е. жидкость становится структурно однородной, состоящей только из разупорядоченной зоны. Существо экстраполяционного метода проиллюстрируем с помощью рис. 1, на котором в полулогарифмических координатах приведена температурная зависимость растворимости водорода в никеле в интервале температур 1200–2630 °С.

На рис. 1 хорошо виден скачок растворимости Н₂, наблюдаемый при плавлении никеля (при 10⁴ Т = 5,79), а также нелинейный

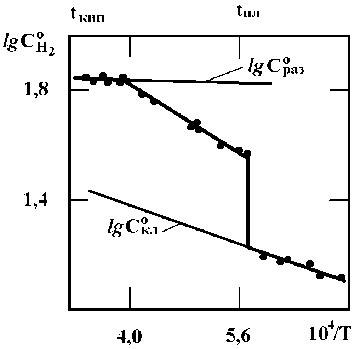
Рис. 1. Температурная зависимость растворимости водорода при Р Н = 1 атм ( С Н см ³ /100 г) в никеле

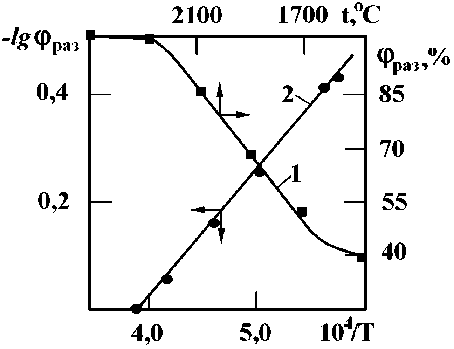
Рис. 2. Температурная зависимость относительной доли разупорядоченной зоны у _раз для жидкого никеля в координатах у _раз - t , ° C (кривая 1)

и lg У раз - 10 4 / Т (кривая 2)

температурный ход растворимости газа в жидком никеле. В общем же температурная 0

зависимость С _Н для рассматриваемого случая может быть представлена в виде двух линейных участков. Изменение угла наклона соответствующей кривой наблюдается при 2300 °С.

Такой температурный ход растворимости водорода в жидком никеле (см. рис. 1) можно представить как результат двух различных температурных зависимостей вкладов в общую растворимость газа, вносимых растворимостью его в кластерах и в разупорядочен-ной зоне.

Предположим, что левый линейный участок кривой рис. 1 отвечает температурной зависимости растворимости Н 2 в полностью разупорядоченном расплаве. Тогда, экстраполируя (линейно) этот участок в область более низких температур, можно получить для них значения растворимости водорода ( С _р ⁰ _аз ) в разупорядоченной зоне. Аналогично, экстраполируя температурную зависимость для твердого никеля (правый линейный участок графика рис. 1) в область более высоких температур, можно получить растворимость Н₂ в кластерах ( С _к⁰_л ) для области существования жидкого никеля.

Определив из графика (см. рис. 1) величины парциальных растворимостей водорода в структурных составляющих расплава ( Ср0аз и Ск0л ) и общую растворимость СН0 , рассчи- таем для любой заданной температуры относительные доли разупорядоченной зоны и зоны кластеров (соответственно ураз и Укл) с помощью уравнений:

/ С Н = С раз -У раз + С кл -У кл ;

^У раз ⁺ У кл = 1.

На рис. 2 (кривая 1) приведены полученные таким образом значения ураз для жидко го никеля при 1453-2500 °С. Величины ураз изменяются от 39 % при 1453 °С (Тпл) до ~ 100 % при 2300 °С.

Как видно из рис. 2, полное разупорядо-чение расплава наступает при температуре, которой отвечает излом на кривой растворимости Н 2 для области жидкого никеля. При этой температуре величины С _Н ⁰ и С _р ⁰ _аз совпадают. Приведенные на рис. 2 результаты по

Ураз прежде всего свидетельствуют о том, что кластеры (сиботаксисы) являются довольно стабильными ассоциациями в расплавах переходных металлов.

Энергия активации в процессе термического распада кластеров, рассчитанная по наклону прямой 2 (см. рис. 2), составляет величину (11,0 ± 3,0) ккал/г∙атом. Найденное значение Ераз в пределах ошибок определений совпадает с таковыми для процессов термического расширения жидкого никеля (7,4–7,9 ккал/г·атом [20]) и его вязкого течения (8,65 ккал/г·атом [21]). Таким образом, определяющим фактором для температурных зависимостей плотности и вязкости является термическое разупорядочение металлического расплава [22].

Применимость экстраполяционного метода ограничивается металлами, не имеющими полиморфных превращений в высокотемпературном твердом и жидком состояниях, и сохраняющих в кластерах тип и параметры атомов кристаллической упаковки. Рассчитанная [16] по политерме стандартной растворимости водорода в никеле температурная зависимость ^ _раз в Ni_ж описывается экспоненциальной функцией

V _раз = 6,7623 ехр ( -4885,2/ R ) . (6)

Найденные величины ^ _раз изменяются от

40 ат. % при t раз = 1450 °С до 100 % при t раз = 2180 °С.

В общем же, по-видимому, экстраполяционный метод (в термодинамическом или кинетическом варианте), может быть применен для аналогичных систем и на основе других объемных структурночувствительных свойств, при распределении которых по структурным составляющим расплавов выполняется правило аддитивности [4].

Учитывая возможность возникновения и весьма длительное существование квазирав-новесных метастабильных состояний жидкости, Б.А. Баум с сотрудниками предложили квазихимический вариант модели микронеод-нородного строения металлических расплавов [6, 23]. В этом варианте прежде всего учитываются три основополагающие идеи: равномерность двух типов движения частиц жидкости, существенная роль сил межатомного притяжения в формировании конденсированного состояния и особенности силовых полей конкретных атомов расплава. При этом особое внимание уделяется учету энергетической неравноценности межатомного взаимодействия атомов разных элементов, что является причиной возникновения кластеров разного состава и строения, обладающих разной устойчивостью во времени.

Результаты изучения температурных, временных и концентрационных зависимостей физико-химических свойств и данные рентгеноструктурных исследований позволили создать физическую модель структуры расплава, рассчитать размер кластеров, определить тип ближнего упорядочения и коэффициент микронеоднородности, температур-

ный интервал устойчивости первичной (после плавления) структуры жидкого металла, температурный интервал и коэффициент интенсивности высокотемпературной перестройки структуры [24, 25].

Дискуссионными являются вопросы, связанные не только с оценкой доли кластерного объема и разупорядоченной зоны, но и с ха-

рактером изменения этих зон при нагреве. Так, по вычислениям Г.С. Ершова и В.А. Чернякова [26] объем разупорядоченной зоны вблизи температуры плавления составляет 3–6 %, а по расчетам И.А. Новохатского и В.И. Архарова [24] – 68 % [15]. По теоретическим предположениям И.А. Новохатского, В.И. Ладьянова и других представителей ква-зиполикристаллической модели строения

жидкости, кластеры полностью разрушаются и жидкость переходит в газообразное состояние при Т раз > 1,55 Т пл , но опубликованы и другие варианты. Однако рентгеноструктурные исследования А.М. Скребцова свидетельствуют лишь об уменьшении размеров кластеров с ростом температуры [27].

Варианты поликристаллической модели жидкости, предложенные Г.С. Ершовым с сотрудниками [26, 28], имеют достаточно разработанный аппарат для количественной оценки структурной и химической микронеоднородности. Получены выражения для

определения количества атомов в кластере ( n ) и его радиуса ( R ) при различных типах

решетки.

В кластере с ОЦК-упаковкой:

n

9 Г А Я исп У

^ОЦК = 16 А Н.

R ОЦК =

к

пл У

( R k

I ³ n ОЦК

V 4

—

к

1 d

1 ' i,

У

где d – межатомное расстояние в жидком ме-

талле.

Для кластеров с гранецентрированной упаковкой атомов:

n ГЦК = 4

R ГЦК =

•

^{< А Я} исп кА Я пл

^{3 П} ГЦК

к

;

У к

—

1 d

¹ ч-

У

Приведенные уравнения можно использовать и для металлов, имеющих гексоганаль-ную плотноупакованную структуру [4].

Анализ выражения (2) приводит к выводу, что для полного количественного описания структурной микронеоднородности однокомпонентной жидкости необходимо располагать лишь двумя величинами: ураз (при какой-либо температуре) и АНраз [29, 30]. С уче- том принципа аддитивности доля разупорядо-ченной зоны при температуре плавления оп- ределяется соотношением

(v раз l

А Н пл А Н раз .

Теплоты разупорядочения жидких металлов в общем случае близки к их энергиям активации самодиффузии и, следовательно, каз L

А Н пл

( Е д)

Д сам

Если величины ЕД неизвестны, то для их оценки можно использовать значения энергии активации вязкого течения (Еп) расплавов. Согласно модифицированному уравнению Стокса – Энштейна [31], коэффициенты само-диффузии Дсам и динамической вязкости (η) связаны соотношением

Д =

к • Т

4 п-р- r

где r – радиус диффундирующих частиц.

Изучая характер температурных зависимостей самодиффузии и динамической вязкости, Д.К. Белащенко пришел к выводу [32]:

Е д = Е _п+ Т .                        (14)

Известно [33, 34], что различным типам кристаллических структур соответствуют и различные механизмы их разупорядочения при плавлении. В.И. Ладьянову, например, удалось использовать характерные значения энтропий плавления. С учетом энтропийного коэффициента аэ = R]AS каз L

R • Т пл

^{( Н} кр L

При таком способе расчета ( ^_раз ) для разных типов кристаллов составляет 0,23–0,46, а температура полного разупорядочения t _раз ~ 1,55 t _пл.

Таким образом, степень структурного ра-зупорядочения при фазовом переходе «кристалл – жидкость» определяется двумя величинами: температурой плавления, которую можно рассматривать как интегральный па- раметр прочности межатомной связи в кристалле, и энтальпией кристалла при этой температуре, характеризующей предельный уровень полученной им тепловой энергии.