О некоторых проблемах преобразования информации в физике твердого тела

Как известно [1], многие физические свойства кристаллов определяет «тонкая структура» их энергетических спектров. Так как энергетические спектры кристаллов недоступны прямому измерению, то для их косвенного определения используют экспериментальные данные о теплоемкости. Связь фононного спектра кристалла с его теплоемкостью, зависящей от температуры, описывается интегральным уравнением первого рода [1]. Поскольку задача численного решения такого уравнения сильно неустойчива, то это осложняет определение «тонкой структуры» фононного спектра кристалла. Как следует из работы [2], применение известных методов регуляризации заглаживает «тонкую структуру» энергетического спектра кристалла. В настоящей работе предложена двойная регуляризация, позволяющая получить равномерное приближение фононного кристалла, а также оценку погрешности этого приближения.

да / \

Sn (е) = [SI - I

i x2

где S ( x ) =----

- , 2 I X

2 sh

d е   C ( 6 )

— = ——; 0 <6<да , е6

; C ( 0 ) - теплоемкость системы; 6 = kT ;

;

T – абсолютная температура;

k - константа, определяемая системой, а n ( е ) - спектральная плотность [1].

Обозначим через H действительное пространство измеримых на [0, да ) функций f ( x ) с нормой, определяемой формулой

C ( ° ) C n ( °)  „                                   _            ,

Предложим, что при —— = ——- е Н существует точное решение n0 (е) е Н П C [0,да) °° уравнения (1), которое единственно и удовлетворяет соотношению n0(е) е Gr, где да 2/ х да

G_r = <  n ( е ) : n ( е ) е Н , j ^{П S} d е + j [ n '( е )]² е d е< r ² > , I                         о ^е о                        ,

а число r предполагается известным, n '( е ) обобщенная производная Соболева от функции n ( е ),

Co ( ° )

но вместо точного значения правой части 0 уравнения (1) известны некоторое приближение

е

C₅ (⁹) _тт                             я a

—^— е Ни уровень погрешности 8 > 0 такие, что

C 8 ( ° )    C о ( ° )

е е

<8 ,

H

где H определено в (2).

Кроме того, предположим, что существует число ео > 0 такое, что для любого е > ео n 0(е) = 0.                                                                                                    (5)

Требуется по исходным данным е0, r, 8 и 8 (@), удовлетворяющим соотношениям (3)-(5), е определить приближенное решение n8(е)еC[0;е0] уравнения (1) и оценить его уклонение от точного решения в метрике max |Vs n8(е)— Vsn0(е)|.                                                                           (6)

• 2.    Метод регуляризации А.Н. Тихонова первого порядка

Метод регуляризации А.Н. Тихонова первого порядка [3] заключается в сведении уравнения (1) к вариационной задаче inf

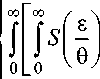
е , _d е - ^{n (е)}— ° е

—

^C 8 ( ° ) I ² °

— + а[[ n '( е )]² е d е + а f n ²( е) — : n ( е ) е Н 1 [0, да ]

°      0                0 ^е

>

где Н 1[0, да] — гильбертово пространство, определяемое нормой да                    да          j

II n ^(е)11 Н ¹ _{[0 да )} = j ^{[ n ,(е)] 2 е d е+} 1 ^{n 2 (е)}”^{, а}> 0.

’       0                    0          е

C ( ° )

В [3] доказано, что для любых значений ——-еН и а>0 существует единственное решение ° nа (е) вариационной задачи (7).

Для определения параметра а в задаче (7) используем принцип невязки [4], который сводит- ся к решению уравнения да

d е- C ₈ ( ° )   d ° =₈

—

°

°

относительно а .

В работе [4] доказано, что при выполнении условия даг cw 1 do >62

0 L ° J ° уравнение (8) имеет единственное решение а(C8,8), а в [5], что при выполнении условия 48 < r справедлива оценка

”r                       -12

J n ₆ « < C ^(E ) - n o^(Е)

_ 0

d E1 2 <

Е

2 r

1 r

1 + JiT—

п2    48

.

Из (5) и (9) следует, что

^Е 0⁰Г                          12

J n 5 ⁵ , ( ^Е ) - n 0^(Е)

d E <    4 r2

^e "i + 4in² - п ²    4 8

.

В решениях n o( e ) и n ^a C ^{8 , 8 )}( e ) сделаем замену переменных, обозначив через x величину

^e/^e o ,

V o^{( x} ) = ⁿ 0 ( ^E/^E0 ) ,

^V 8 ( ^x ) = ^{n a} ( C ^{8 , 8 )} ( ^E/^E0 ) ^.

Из (10)–(12) следует, что

12 dx < x

4 r ²

1     2 r

1 +ln --- п2    48

.

Так как

1                            ₂       1                     dx

J[ 4xv ₅ ( x ) - xV V o ( x ) ] dx <  J[ V ₅ ( x ) - V o ( x ) ]² — ,

0                                0x то из (13) следует, что

4 r ²

1     2 r

1 +у ln --- п2    48

.

При этом условии (3) перейдет в следующее

¹ v ²( x )       ¹ '

f —--- dx + J [ v ₀ ( x )]² xdx <  r ².

₀ x        ₀

Теперь оценим норму    xv ₀ ( x ) ₁ в пространстве W ₂¹[0,1] функции x v ₀( x ).

2      1                  1 г

I W 1 = J x^V 0 ( ^x ) ^{dx +} f (v x ^V 0 ( x ) )

²    0               0 L

dx =

¹              1 ¹ v ² ( x )

= J xv ₀ ( x ) +—j —--- dx +

0           4 0 x

J v ₀ ( x ) v ₀ ( x ) dx + J Г v ₀ ( x ) J xdx . 00

Из неравенства Коши – Буняковского следует, что

¹          _'              1 ¹ v ² ( x )        1

I ^V 0 ( ^x ) ^V 0 ( ^x ) ^dx < - I----- ^{dx +} -

₀                 8₀ x 2

Из (16) и (17) следует, что

₂     1              12          1         ₂

11^ ^V 0^{( x} )L < J ^xV 0^{( x} ) ^{dx +}o J dx ⁺ 7J [ ^V 0 ( ^x ) ] ^xdx .

^W 2    ₀            8 ₀ x 2 ₀

Так как

^{1                1} v ²( x )

j xv 0( x ) dx <  j —--- dx ,

0              0x то из (18) следует, что

xv 0 ( x ) _W ² ₂1

3 ¹ v ² ( x )      3 ¹_'      ²

< — I ⁰    dx + — I I v ₀ ( x ) I xdx ,

2 0 X 2 0 ^{L J}

а из (15) и (19), что

и v o ( ^x ) W <  2 r ².

• 3.    Решение задачи восстановления непрерывной функции,

заданной со среднеквадратичной погрешностью

Из (14) и (20) следует, что нашу задачу свели к известной задаче восстановления непрерывной функции, заданной с погрешностью в пространстве L ₂[0,1].

В дальнейшем введём обозначения

и(x) = Vxv(x);   x е[0,1], r = . /| r, ц = .   22=

1 + -vln

V   п24

Предположим, что неизвестная функция и о ( x ) е C [0,1] и удовлетворяет условию 11

J и 0 ( x ) dx + J [ и ₀ ( x )]² dx <  r 1 ²

и известна функция g _ц ( x ) е L ₂[0,1] и уровень погрешности ц такие, что

||g ц ^{( x} ) - ^и о^{( x} )| L <ц .

Требуется по исходным данным g _ц , ц и r 1 , удовлетворяющим (21) и (22), определить функцию и _ц ( x ) е C [0,1] и оценить величину уклонения Ц и _ц ( x ) - u ₀( x )||_с.

Для решения данной задачи используем метод усредняющих функций, описанный в [6].

Рассмотрим усредняющую функцию

ю( y)= •

1 e

Y

1 - У ²

,

0,

I у1 ^ 1,

1 где y = J e

- 1

^{1 - У 2} аУ .

По функции ю ( у ), определенной (23), для любого h >  0 зададим функцию

^ю h ⁽ У ) = ¹ ®f— h

v h J

у е R.

Теперь, используя функцию ю h ( у ), определим регуляризующее семейство { P h : h >  0 } линейных ограниченных операторов, отображающих пространство L ₂[0,1] в C [0,1]

P h g ⁽ У ) = J g ⁽ У ) ^ю h ^{( x -} У ) dy ;      ^{и (} У ) ^е L 2^[0,1].

.

В одной из лемм, доказанных в [6, с. 47], следует, что для любого h >  0 PP_h || < — V Y h

Обозначим через M_r множество из пространства C [0,1] и определяемое формулой

1                         1

M r 1

< u ( x ): u ( x ) e ^[0,1], j u ²( x ) dx + j [ u '( x )]² dx <  r^ > ,

0              0

а через u ₀ ^h ( x ) – функцию, определяемую формулой u h ^{( x} ) = P h u 0^{( x} ).

В [6, с. 67] доказано, что

II u o ^{( x}) - u o h ^{( x} )|| _{c [01]}<  ^r 1 V h .

Окончательно, в качестве приближенного значения uц (x) восстанавливаемой функции u0(x) возьмем функцию u ц ( x ) = Ph (ц) g ц ( x ), в которой hц определено формулой

h (Ц) =-ц

.

r iV Y

Учитывая, что

I ^u ц ^{( x} ) ^{- u} 0^{( x} )| L [0,1] < | u 0^{( x} ) ^{- u} 0 h ^{( ц ) ( x} )|| ⁺ I P h ( ц ) 11 • Ц , где h ( ц ) определено формулой (24), получим

II u ц ⁽ x ) ^- u ^{о (} x )|| _с [0,1] < ²^2" .

Теперь, сделав замены, обратные (11) и (12), мы получим решение n 5 ( е ) уравнения (1)

n5(е) =

Vе? uц (Е/Е0 )

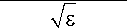
Тогда из (6), (25) и (26) следует, что

max I E n n 5 ( е ) - VE n ( е ) I < , Ee [0, E 0 ]l                  ⁰ I ^О? ¹²

1 r

1 + —7 ln²-- п ²     4 5.

- 1

.