О некоторых свойствах амплитуды рассеяния

В теории рассеяния важная роль отводится амплитуде рассеяния (ар), или как ее еще называют в англоязычной литературе "фактору углового распределения" (far field pattern) (см., например, [1]). Использование понятия амплитуды рассеяния, как показывает практика, может существенно упростить решение многих задач и сделать его гораздо более прозрачным физически. При этом весьма полезно использовать различные представления амплитуды рассеяния и ее аналитические свойства. В настоящей работе приводится ряд полезных определений и свойств амплитуды рассеяния, рассматривается влияние ее спектра на расчет поля в волновой зоне.

РАЗЛИЧНЫЕ ОПРЕДЕЛЕНИЯ АР

Математическое определение ар следует из следующей теоремы (см., например, [2]): всякое решение уравнения Гельмгольца, удовлетворяющее уравнению Гельмгольца и условию излучения Зоммерфельда на бесконечности, имеет следующее асимптотическое представление через уходящую сферическую волну

u ( x ) =

ikx e

x

u „ ( x ) + O

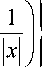
| x| > ^,

где u _m ( x ) — фактор углового распределения поля. u _т ( x ) в общем случае определяется выражением [1, с. 499], [2, с. 20]

^u » ^{( x} ) = 7- f j ^{u (} У ) ^{4 п} aD I

d e "^ikx y ^{d n (} У )

d u ( y ) ^{d n (} У )

e ~^ikx^y ^ d s ( y ). (2)

Здесь x = ( x 1 , x ₂, x 3 ) e R ³ — точка наблюдения;

x = p x - eQ — единичный вектор на сфере Q единичного радиуса; D — некая ограниченная область, включающая рассеиватель или излучатель с границей d D ; n — внешняя нормаль к d D ; k = to / c — волновое число. Если u ( x ) обозначает давление, то для u _т ( x ) из (2) справедливо равенство [3, с. 109]

^u „^{( x} ) = ^- 7- ^х

4 п х j {ikx - n(y)p(y) + itopn(y) • v(y)} e-ikxyds(y). (2а) ad

Здесь v ( y ) — вектор колебательной скорости на поверхности d D .

Когда речь идет о рассеянии, то подразумевается наличие суммы падающей и рассеянной волн u (x) = ui (x) + us (x), где падающая волна обычно полагается плоской

_ ikx • d ui = e , а рассеянная волна us (x) удовлетворяет условию излучения Зоммерфельда. В этом случае фиксируется зависимость рассеянной волны от направления распространения падающей волны d us(x) = us(x,d)

и, следовательно, аналогичная зависимость ар u „ (xc) = u „ (^x, d).                 (3)

Очевидно, что в случае, когда падающая волна представляет собой совокупность плоских волн

u ( x ) = j g ( d ) e kx'd d s ( d ),           (4)

Q '

ар вычисляется следующим образом u„ (x) = J g(d)u„ (x, d)ds(d) •           (5)

Q '

Здесь Q ' — область определения падающей волны.

Известно [4, с. 83], что любое дважды дифференцируемое решение однородного уравнения Гельмгольца есть аналитическая функция своих аргументов. Решение однородного уравнения Гельмгольца, определенное на всем пространстве x е R3, называется целым решением [2, с. 19]. Отсюда: целое решение уравнения Гельмгольца, удовлетворяющее условию излучения Зоммер-фельда, равно тождественно нулю. Решение однородного уравнения Гельмгольца, область определения которого лежит вне некоторой сферы конечного радиуса, называется излученным решением (radiation solution), если оно удовлетворяет условию излучения Зоммерфельда lim r I--iku | = 0, r = Ixl r^ю

и предел достигается равномерно для всех направлений x / x .

Справедливо утверждение [2, с. 33]: пусть u(x) есть излученное решение уравнения Гельмгольца вне шара |x| < R, R > 0. Тогда для u(x) справедливо разложение по сферическим функциям to n

u ( x ) = k ZZ ah ⁽¹⁾( k|x|)Y„ ^m ( x ).      (7)

n = 0 m =- n

Здесь h _n ⁽¹⁾( kx ) — сферическая функция Ханкеля первого рода; a _n ^m — постоянные коэффициенты; Y _n ^m ( x ˆ) — сферические функции на единичной сфере, равные

Y n^m ( θ , ϕ )

2 n + 1 ( n - у 4 к ( n +

m )!

P_n ^m ( θ ) e ^{im ϕ} . m )!

Полю (7) отвечает амплитуда рассеяния [2, с. 34]

to 1 n u.(x) = Z n Z a."Y."(x)■         (9)

n = 0 i     m =- n

Если излученное поле обладает сферической симметрией, то справедливы следующие выражения [5, с. 223, 224]:

to

^{u ( x} ) = ^k Z a n h n ^<1)( k l x l) P n (cos ⁶ ) ,         ^(7а)

n = 0

to ₁

^u to ^{( 6} ) = Z- n + a n P n (cos ⁶ ).              ^(9а)

n = 0 i

Справедливо следующее равенство [2, с. 31], [1, с. 434]:

e- i-d = Z i n (2 n + 1) j n ( k|x |) P n (cos Y ) = n =0

to n                                             *

= 4кZin Z jn(—W)Ynm(x)(Ynm(d)) = n=0 m=-n

= Z {in (2n + 1)Z £m (n m)! cos m(Ф - в) x n=0            m=0 (n + m)!

x j n ( k| x |) P n^m (cos 6 ) P n^m (cos а )},           (10)

x е R ³.

Здесь γ — угол между векторами x и d ;

[ 1, m = 0

£_m = <          — множитель Неймана. В (10), в

m

[ 2, m ^ 0

частности, использована теорема сложения [2, с. 26]:

'ZY . ^m ( x ) ( Y, " ( d ) ) ' = 2 n ^{+ 1} P n (cos Y ). m =- n                      ^{4 П}

Уиттекером установлена следующая формула разложения по плоским волнам для целых решений однородного уравнения Гельмгольца [6]:

u ( x ) = — j n d e J й(d ) e kd ' ^x sin а d а ,    (11)

4 π ₀₀

где d = (sin а cos в ,sin а sin в ,cos а). Причем для элементарных целых решений Л m (x) = = jn(k|x|)Ynm(jx) имеет место равенство л m (x)=j; (—\x\) y" (6, Ф)=

2 ππ

= ( - i ) ⁿ — J d в J Y n^m ( а , в ) e ^-kdx sin а d а .   (12)

4 π ₀₀

Тогда, если разложить образ uˆ(d) по сферическим гармоникам ton i/(d) = u(а, в) = Z Z (-i)na:Y„m (а, в),    (13)

n=0 m=-n то окажется, что прообраз равен ton u (x) = kZZ amЛm (x).         (14)

n = 0 m =- n

Для a _n ^m имеем:

2ππ anm = i" J dв J( Y™ (а, в) )* u (а, в )sin а d а .    (15)

Как видно, решению (14) соответствует образ (13) с коэффициентами, определяемыми из (15). Разложение осуществляется по однородным плоским волнам с углами распространения из так называемого круга видимости 6 е[0, п ], ф е[0,2п ], что отвечает компонентам волнового числа kx. = ksin 6 cos ф и ky = k sin 6 sin ф, не превосходящим   k , т. е. лежащим внутри круга kx 2 + ky 2 < k2. xy

Равенство (12) означает, что с точностью до постоянного коэффициента функция Y _l ^m ( α , β ) является Фурье-образом функции j _l ( kr ) Y _l ^m ( θ , ϕ ) в круге видимости. Преобразование Фурье от функции Y, ™ ( а , в ) на всей плоскости ( k _x , k y ) е R ² равно [6]:

П m ( x ) = h " « ( k\x\ ) Y "m ( 6 , Ф ) =

π

• 2 п 2

= (- i ) n +1 _L [d в f Y nm ( а , в ) e kd " x sin а d а .     (16)

2π 00

По мнению автора, в последнем выражении в работе [6] ошибочно фигурирует множитель ( - i ) " вместо ( - i ) " ^{+ 1}, что легко проверяется рассмотрением асимптотик обеих частей выражения при | x | ^ да .

Показатель экспоненты в (16) равен d • x = |x| (sin 6 sin а cos(ф - в) ± cos 6 cos а), а знак + соответствует положительной ординате точки наблюдения x , знак "минус" — отрицательной. Если теперь ввести преобразование Фурье [6]

π

"k 2      2

u ( x ) = — I'd в  I" й ( d ) e ikd " ^x sin а d а =

2π 00

. CO CO

=-и

2 π

-да -да

u ˆ( k _x , k _y ) k _z

ek'x d k_x d k_y xy

и воспользоваться разложением образа uˆ(d) по сферическим гармоникам да 1 n

Ui(d) = й(а, в) = EE aXm (а, в), (18) n=0i    m=-n то получаем для поля u(x):

да n u (x)=kee amn m (x)= n=0 m=-n да n

= k EE a^ n ⁽¹⁾( k|x|Y ( 6 , Ф ).     (19)

n = 0 m =- n

В (17) k z = ^ k ² - k _x ¹ - ky¹ = k cos а — вертикальная составляющая волнового вектора.

Сравнивая (19) и (7), а также (18) и (9), делаем ожидаемый вывод о том, что амплитуда рассеяния в области видимости совпадает со спектром поля (19) в разложении (17):

U да ( DC ) = ?ⁱ( DC ).

Отметим, что a _n ^m из (18) определяется так:

a m = i ^{n + 1} J d в J ( Y _n ^m ( а , в ) ) * й( а , в )sin а d а . (20) 00

Отметим также, что поле (19) удовлетворяет при x ^ 0 однородному уравнению Гельмгольца и условию излучения Зоммерфельда, что означает, что u ( x ) является излученным полем.

Сравнивая выражения (11) и (17), видим, что в представлении целого решения (11) присутствуют только однородные плоские волны. В аналогичном представлении излученного решения (17), кроме того, присутствуют неоднородные плоские волны, что обеспечивает соответствующее поведение решения при | x | ^ 0 . Для изучения влияния вклада неоднородных плоских волн в представлении (17) при | x | ^да перепишем (17) в следующем виде:

π ik 2 п      2 - iда

u (| x |, 6 , ф ) = — jd в J й( а , в ) e ikd • ^x sin а d а = 2 π ₀₀

= u p ^{+ U} e ,

•    sin а d а ,

Up = iT" f d в J й( а , в ) e

2π00

ik 2 п     2- i 'i ue =— [ d в [ ui (а, в) eikd' x sin а d а.

2тг

π _{0 π}

Здесь u p — составляющая поля, включающая только однородные плоские волны; ue — составляющая поля, включающая только неоднородные плоские волны. Оценка асимптотического поведения up и ue при |x| ^да изучена в работах [3, 7], где получены следующие результаты (поведение поля равномерно по ϕ ):

In П I

— при ti e 0,—  имеет место асимптотика

( 2 J

U p = O (| х |^_1) и U e = O ( х ' J;

π

— при ti = 0 и при ti = — имеет место асимптотика U p = O (| х | ') и u_e = O (| х | *).

Поскольку выбор направления осей координат носит произвольный характер, то аномальное по-π ведение ue при ti = 0 и ti = — носит нефизический характер. Поэтому следует признать, что асимптотика общего поля и при |х| ^ да в целом совпадает с асимптотикой поля up , в котором присутствуют только однородные плоские волны.

АНАЛИТИЧЕСКИЕ СВОЙСТВА АР

Аналитические свойства амплитуды рассеяния рассматривались в работах [3, 4] и независимо в работах [8, 9]. При изучении аналитических свойств амплитуды рассеяния исходят из ее формального определения (2а) либо из определения через объемный потенциал [1, 2, 3 и др.]:

^и да^{( х} ) = ^-     J g ⁽ У ) ^e"k™'y d У .

4 π _D

Исходя из этих определений, получены следующие свойства амплитуды рассеяния как аналитической функции, представляемой поверхностным или объемным интегралом:

— амплитуда рассеяния и _да ( к _х , k y ) в переменных k _x , k _y является аналитической функцией комплексных переменных k _x , k _y , исключая точку ветвления а = 0 функции а = ^ к ² - к _х ² - k y ² , т. е. на круге к_х ² + k y ² = к ²;

— амплитуда рассеяния и _да ( ti , ф ) в переменных θ , ϕ является аналитической функцией комплексных переменных θ , ϕ при всех значениях θ , ϕ , т. е. является целой аналитической функцией этих переменных.

Отсюда важное следствие: если амплитуда рассеяния задана внутри области видимости ti e [0, п ], ф e [0,2 п ], то вне этой области она может быть продолжена аналитически единственным образом. Это в том числе означает, что если и _да ( 9 , ф ) не равна тождественно нулю внутри области видимости, то она не может быть равна тождественно нулю вне области видимости.

Существует альтернативное определение аналитических свойств амплитуды рассеяния [4, 10].

Введем обозначение и „ (X) = F0(9, ф).                (23)

Справедлива следующая теорема, полученная Аткинсоном и Уилкоксом [4, с. 84]: пусть u(x) — излученное решение (т. е. удовлетворяет уравнению Гельмгольца вне сферы радиусом R и условию излучения Зоммерфельда при |х| ^да). Тогда при |х| > R справедливо равенство eiM   f (0, ф)

и ( х ) = —- >   ----,

Iх £ И"

где F ₀ ( θ , ϕ ) определяется из (23), а функции F _n ( θ , ϕ ) определяются из следующего рекуррентного соотношения:

F n = — ^х 2 ink

I z п 1 d        д 1 d2 I х n(n-1) +--(sinti —) +---5--IFn-1. (25)

v sin ti дti       Sti    sin2 ti дф J

Равенство (24) при | х | >  R сходится абсолютно и равномерно, его можно дифференцировать по x , θ , ϕ почленно любое число раз, и полученные после этого ряды также сходятся абсолютно и равномерно.

Справедливо также следующее утверждение (теорема Мюллера) [10], [4, с. 201]. Пусть ида (ti, ф) = F0(ti, ф) — амплитуда рассеяния (диаграмма направленности), соответствующая объекту, расположенному внутри сферы |х| < R. Тогда существует гармоническая функция h , определенная во всем пространстве R3 и такая, что а) h (1, ti, ф) = и да (ti, ф);

б)

2 ππ

J J h ( r , ti , ф )|2 sin ti d ti d ф — есть целая функ- 00

ция переменной r экспоненциального типа, не превышающего R , (целая функция есть функция

экспоненциального типа, если ее модуль при |r | ^да на комплексной плоскости r растет не быстрее e° r ; а >  0 — есть тип этой функции).

РАССЕЯНИЕ В СЛУЧАЕ, КОГДА ПАДАЮЩАЯ ВОЛНА ОТЛИЧНА ОТ ПЛОСКОЙ ВОЛНЫ

Выше выражениями (4), (5) была установлена зависимость результирующей амплитуды рассея- ния u∞(xˆ), когда известна амплитуда рассеяния u∞(xˆ,d) при падении на рассеиватель плоской волны по направлению d и спектр g(d) падающих на рассеиватель плоских волн. Кроме того, выше было установлено, что вкладом неоднородных плоских волн в амплитуде рассеяния при расчете поля рассеяния в волновой зоне можно пренебречь. В связи с этим откорректируем выражение (5) применительно к расчету поля рассеяния в волновой зоне при падении на рассеиватель волны (4) со спектром g(d). Рассмотрим два случая. Случай, когда падающей волной является однородная плоская волна, и случай падающей неоднородной плоской волны. Для дальнейших рассуждений полезным окажется соотношение взаимности [1, с. 127], [2, с. 53], [3, с. 261]:

u _∞ ( x ˆ, d ) = u _∞ ( - d , - x ˆ).             (26)

Во-первых, в силу сказанного выше об отсутствии влияния на асимптотику поля в волновой зоне спектра u _∞ ( x ˆ) вне области видимости сразу ограничим спектр x ˆ в (5) областью видимости x ˆ ∈ Ω _p . Здесь Ω _p — область видимости θ ∈ [0, π ], ϕ ∈ [0,2 π ]. Далее с учетом (26) преобразуем (5):

u _∞ ( x ˆ) = ∫ g ( d ) u _∞ ( - d , - x ˆ)d s ( d ) =

Ω ^'

= ∫ g ( d ) u _∞ ( - d , - x ˆ)d s ( d ) + ∫ g ( d ) u _∞ ( - d , - x ˆ)d s ( d ). Ω p Ω e

Из этого равенства следует, что последним интегралом можно пренебречь, т. к. он представляет собой сумму амплитуд рассеяния с областью определения вне зоны видимости: Ω _e — область, лежащая вне зоны видимости. Таким образом, с учетом сказанного для расчета асимптотики поля в волновой зоне в (5) достаточно ограничиться областью интегрирования Ω _p :

u _∞ ( x ˆ) = ∫ g ( d ) u _∞ ( x ˆ, d )d s ( d )

Ωp при условии xˆ ∈Ωp .

ВЫВОДЫ

Приведенные в работе данные позволяют эффективно пользоваться аппаратом амплитуд рассеяния в интересах решения различных волновых задач, включая и такие задачи, как расчет радиа- ционного давления на частицы в произвольном акустическом поле.

Настоящая работа выполнена при поддержке фонда РФФИ, грант № 05-03-33108 и целевой научно-технической программы Российской Федерации "Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007–2012 годы", лот 2, шифр "2007-2-2.2-04-08".