О некоторых свойствах бигармонических функций в R2

polyharmonic functions, Green's

Шароф Ярмухамедов занимался исследованием классической интегральной формулы Грина для гармонических функций в неограниченной пространственных областях. Задача заключалась в получении формулы Грина для растущих гармонических функций. Здесь вместо классического фундаментального решения уравнения Лапласа надо было построить новое фундаментальное решение, которое достаточно хорошо убывает на бесконеч- ности. Ш.Ярмухамедовым было построено требуемое фундаментальное решение в явном виде, которое выражается через целой функции комплексного переменного. Им получена интегральная формула Грина в неограниченной области в классе растущих гармонических функций. В этом направлении им было установлено теорема типа Фрагмена - Линделефа для гармонических функций.

В этой работе используя ядро Ярмухамедова получая интегральное представление для неё получаем оценку роста функции внутри области т.е теоремы типа Фрагмена – Линделефа.

Интегральное представление в R2 для бигармонических функций заданные в области D которую мы намерены получить, иными словами, по граничным значениям функции восстановить ее значения всюду внутри области выражает фундаментальное свойство для бигармонических функций.

Пусть R² - двухмерное вещественное евклидово пространство, x = (x i > Х 2 )> x ' = (x i > 0), r = |x - y|> s = |x ' - y ' |> a² = s>

d = {y:y = (У1,У2),yi e R, о < У2 < О = П> P > о}.

Функцию Ф ^ Су, x) при s > 0, ст > 0, a > 0, определим:

oo     exp(aw+w²)-achip₁(w- h )

Фа(у, x) = Cn,m f^ Im I----I (u2 - s)du, w = iu + Vs             Ы-Х2

У 2 ,(3)

где C_n , _m = (8пГ²(2))  , можно доказать что эта искомая функция.

Теорема 1. Ф ^ Су, х) является полигармонической функцией порядка 2 по у при s > 0 и для этой функции имеет место

Фа(у,х) = ^o(r2 for + С^у)), где  Ga(y,x)  регулярная по переменному у и непрерывно дифференцируемая на D.

Доказательство.

Для того, чтобы получить утверждение теоремы, рассмотрим подынтегральное выражение

J_i = Im

exp (a" + " 2 — acosp_i

("-й)

w -% 2

имея ввиду свойства гиперболических функций, получим

exp( a" + "2 — acospi (" — h)) =

= exp [a(iu + y 2 ) + (iu + У 2 )² — acosp i (iu + У 2 — h )] = exp [ay 2 + У 2 ² — u² —

—a⁽chp i u⁾ (cosp i (y 2 — h )) + i (au + 2uy 2 — a ⁽ shp i u) (sinp i (y 2 — h )))] =

= exp [ay 2 + У 2 ² — u² — achp i ucosp i (y 2 — ^h)] exp i (au + 2uy 2 — ashp i usinp i (y 2 — ^h)) = exp [ay 2 + y 2 ² — u² — achp i ucosp i (y 2 — ^h)]

( cos (au + 2uy 2 — ashp_iusinp_i (y₂ — -))

+ isin (au + 2uy 2 — ashp_iusinp_i (y₂ — 2)))

^i = ay2 + y22 — u2 — achpiucospi (y2 — h)

^ 2 = (au + 2uy 2 — ashp i usinp i (y 2 — ^))

Применяя некоторые свойство комплексных чисел

а+ib   cb-ad

Im = ——- = Im c+id    c2-d2

получим:

а+1-l+ib _ cb-(a+i-i)d

c+id

c²-d²     ,

| exp( ----

aw+w²-acosp !

W-X 2

H)) ] = _Im|.

exp(aw+w²-acosp !

W-X 2

(^-^-i+ij

Поэтому

| exp( ----

aw+w²-acosp !

W-X 2

нН+кпШ.

W-X 2

Ф^У^) =

СО

С о I Im vs

exp

(ow + w2

— acosp 1

^(w— 2))

— 1

W — X 2

(u2 — s)du

+ cA Im [ —] (u²

— s)du

VS    w —X2

Кроме того разделяя последний интеграл на две части и вычисляя

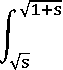
u u² + ⁽ У 2

—

^V 1 ^+S       u

I TV7------VI (u2 — s) du

_V S    u² + ⁽ У 2 ^{— x}2^{) 2}

u² + ⁽ У 2 — X 2^{) 2} = t, u² — s = t — r²

-^2 (u2 — s)du = I x2)2                   r

^1+r 2 (t-r²)dt__i

—

. 2

t

r2

f ^1+r 2 dt r^{2      t}

= 1 + 2r2lnr — r2ln(1 + r2)

имеем

Ф a⁽ У,x ⁾ = С о

О

| Im vs

exp

(ow + w2

— acosp 1

^(w— 2))

—

w — x2

(u2 — s)du +

[-------] (u2 — s)du + c0 I Im [-------] (u2 — s)du

Lw — x₂                   i+s w — x₂

Если обозначим

О

G a⁽ У,x ⁾ = C о^| Im vs

exp (ow + w2

— acosp 1 (w — h)) — 1

w — x 2

(u2 — s)du + 1

— r2ln(1 + r2) + c0 I Im [-------] (u2

— s)du

V1+S    w —x2

то

Фa(y,x) = c0(r2lnr + Gст(y,x))

где G 2 (x,y, ст)-будет в свою очередь гармонической, легко доказать что это функция полигармонической функцией порядка 2 по у при s > 0.

Теперь мы докажем утверждение:

Ф^(у,*) = c0(r2 lnr + G1(х,y, ^))-бигармоническая функция.

Лемма 1.1.2. Если ф_а(у,х) гармоническая функция в R ^m по переменной у включая и точку х, то справедливо равенство

^гкфа(у,х) = гк-2фа,1(у,х) где

фа,1(у,х) = к(т + к — 2)фа(у,х) + 2к%т=1(У] — Xj)^^

функция тоже является гармонической функцией в Rm по переменному у включая и точку х.

Теорема 2. Для функции Фа(у, х), имеет место неравенства:

№„(y,x)l < (1+1);zj7, A = achapi \ Г      /X X J (A )

Доказательство.

m

Фо(У,х) = Со1 Im vs

exp (o⁽iu + y 2 ) + ⁽iu + y 2 ^{) 2} — achip 1 (⁽iu + y₂) — h)))

⁽iu + У 2 ) — Х 2

r ² dt

u2 — s = r2t, udu = r2dt, du = , „

Vr ² t+s Ф а СУ^Х)

m

= I Im

(u² — s)du,

exp (o(iJr²t + s + y₂) + (iJr²t + s + y₂) — acosp 1 (iJr²t + s +y₂ —

5)1

(i-JrH+s + y 2 — Х 2 )

r4tdt

Vr2t + s

При A1 = ay2 + y22 — r2t — s — achp1Vr2t + scosp1 (y2 — h) ^2 = ((^ + 2y2)4r2t + s + —ashp1^r2t + ssinp1 (y2 — -))

Фя(У,х)

Q = exp(vy2 + У22}

= I Im

Q(cosA₂ + isinA 2 )(y₂ —x₂— iVr²t + s)

^exp (^J^⁰^ ^(y 2 ^{— 2} ) ⁾ e ^xp( r 2 _t + _S )( ^y ₂ ^{— x} 2 + .S^^ ^{— x} 2 ^— ;..  +•■

r4tdt

Vr2t + s

O

Фа^х) = r² I 0

Q(y2 — x2)sinA2 — Vr2t + scosA2

tdt

CO

= r2 I

exp (achp₁Sr²t + scosp 1 (y₂ — h)) (t + 1)exp(r²t + s') ^^{r t + s}

Q⁽y 2 — X 2 )sinA 2

tdt

exp (achp^rt + scosp 1 (y₂ — h)) exp(r²t + s)(t + 1) ^^{r t + s}

--

O

—r2 I

QcosA2

tdt

(                      (     h\\ ,     , exp(r2t + s')

exp achp₁\r²t + scosp 1 {y 2 ^-2))^{(t + 1)}

Обозначая

Фo(У,x} = r2]1 -r2J2

где

J 1= £

Q(y2-x2)sinA2

tdt

exp(achp 1 Vr² t+scosp 1 (y₂ - h ))exp(r² t+s)(t+1) ^Sr 2 ^t+s

CO

Ji=]

QcosA2

tdt

/                            h\\       . exp(r2t + s')

exp I achp₁vr²t + scosp 1 (y 2 -2)) ^{(t + 1)}

4 = 0У2 + У22

- S

-

achp1acosp1 (у - -)

l/ 1 \= J o”

1 (y 2 -X 2 )Vt

QsinA 2

(t+1) Vr2t+s

exp( achp-^r ² t+scosp₁(y₂ - h ))

Vtdt exp(r ² t+s)

<

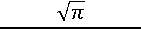
r ²⁽¹⁺2) exp(A)

_ 1

” t ^p 2 dt

⁰   exp(at)

1^11    r3 exp(4)

...(2p-1) ул    ”     dt

2 ^p     „Р+ ,  0 exp(r ² t+s)

a 2

c

”

\J 2 \ = I

t

^(t + 1) exp

QcosA 2

(achp₁4r²t + scosp 1 (у₂ — h))

dt

co

exp(r²t + s')   r² exp(A)

Итак, \Фа(у, x)\ < (4 + 4) ^2^ = (1+ 1) ^77, °             r3   r2 exp(A)     r       exp(A)

Вывод: В этой работе используя свойств ядро Ярмухамедова построив функцию Карлемана получим интегральное представление т.е интегральная формула Грина в неограниченной области в классе растущих бигармонических функций. Интегральное представление в R2 для бигармонических функций заданные в области D которую мы намерены получить, иными словами, по граничным значениям функции восстановить ее значения всюду внутри области выражает фундаментальное свойство для бигармонических функций и для неё получаем оценку роста функции внутри области т.е теоремы типа Фрагмена – Линделефа.