О некоторых свойствах газовых течений с осевой симметрией

Закрученные осесимметричные течения представляют собой важный частный случай пространственных течений, описывающихся двумерными уравнениями. С одной стороны, в них в полной мере проявляется сложная связь радиально-осевого и окружного движений. С другой стороны, осевая симметрия накладывает дополнительные связи на параметры движения, которые упрощают исследование по сравнению с общим трехмерным случаем. Реальные конструкции редко бывают полностью осесимметричными. Но проверка закономерностей осесимметричных потоков может быть полезна для верификации численных методов расчета трехмерных схем, когда такие схемы используются в осесимметричном случае. Поэтому исследование закрученных осесимметричных течений представляет не только теоретический, но и практический интерес.

В дальнейшем все рассматриваемые функции считаются достаточно гладкими, насколько это требуется проводимыми математическими операциями и рассуждениями. Это относится либо целиком ко всему течению, если в нем нет скачков уплотнения, тангенциальных или слабых разрывов, либо к зонам течения, расположенным между скачками и разрывами. Для краткости будем называть такие зоны зонами гладкости .

Рассмотрим осесимметричное течение идеального газа в потенциальном поле внешних сил. Обозначим: V - вектор скорости, р - плотность, p - давление, И - потенциал массовых сил, Q = rotV - завихренность. Движение газа описывается уравнениями Эйлера, которые можно записать в форме Громеки–Ламба [1]:

£ + q х V = -^V-V (V 2 + и) , (1) at р \ 2

дР + div( р V ) = 0 . (2)

Введем цилиндрическую систему координат r, ϕ, z с началом в точке O и осью Oz , совпадающей с осью симметрии. Пусть e _r , e ϕ , e _z – правая тройка единичных векторов в радиальном, окружном и осевом направлениях соответственно. Вектор скорости имеет вид суммы: V = V r e _r + V ^ e _ф + V z e z = V _r + V _ф + V z , где его компоненты по осям V r , У ф и V _z , как и другие газодинамические функции, зависят только от координат r , z и от времени t . Очевидно, в этом случае градиент в правой части уравнения (1) имеет нулевую ϕ -компоненту. Закрученное осесимметричное течение имеет отличную от нуля окружную скорость У ф . Величину ү = 2 nrV ^ назовем окружной циркуляцией.

В силу осевой симметрии ( дф = о), меридиональная составляющая завихренности Q _rz , равная векторной сумме радиальной и осевой составляющих ( Q _rz = Q _r + Q _z ), является ротором окружной скорости V ϕ . Аналогично, окружная составляющая завихренности Ω ϕ является ротором меридиональной скорости V _r + V z :

Q rz = rot V _ф ,     Q ф = rot ( V r + V z ) .

Учитывая, что

Q ф х V ф — 0 ,    Q rz x

V ' = -v( V O - R -

получим

Q х V = Q _rz х ( V _r + V _z ) + Q _ф

' (V "  ^V ' -V (V ²) - (V ²) e■

Первое слагаемое в правой части направлено вдоль e _ϕ , а последние три лежат в меридиональной плоскости, проходящей через ось симметрии. Поэтому уравнение (1) равносильно системе двух уравнений:

^^ + Q ф х (V.r + V z ) = ^V-V (V4 + V4 +и) + ('Я e Г,(3)

dt                                      р \ 2      2

-dt^ + Qrz x (Vr + Vz)= 0.(4)

Уравнение неразрывности (2) в цилиндрической системе координат имеет вид др + d ( рУг ) + !V + 4 (рVz ) = 0.(5)

∂t ∂r         r ∂z

Уравнения (3) – (5) являются основными уравнениями, описывающими закрученные осесимметричные течения сжимаемого газа. Для замыкания их нужно дополнить еще одной связью, например выражающей адиабатичность течения, то есть сохранение в движущейся частице энтропийной функции _ρ ^p _k ,где k – показатель адиабаты.

Иногда течение считают потенциальным, то есть безвихревым: Q = 0. Иногда - баротропным: р = f ( p ). И так далее. Но некоторые общие свойства осесимметричных течений следуют из уравнений (3) – (5) без каких-либо дополнительных предположений. Поэтому ниже, если не оговорено иного, рассматривается самый общий случай, когда течение считается неадиабатичным, небаротропным и завихренным.

3.    Закрученность и завихренность

Рассмотрим течение в зоне гладкости (см. выше). Если зона гладкости содержит (хотя бы частично) ось симметрии, то на оси, в силу непрерывности, окружная компонента скорости V ϕ должна обращаться в нуль. Воспользуемся этим обстоятельством.

Легко проверить, что меридиональная составляющая завихренности: Q rz = Q r + Q z и окружная циркуляция: ү = 2 nrV ^ связаны между собой соотношением

Q rz = - 2ППГ [ e ф ^х^ү ] • (6) При отсутствии завихренности равна нулю любая ее составляющая, в частности: Q rz = 0. Поэтому из (6) следует, что в безвихревом течении окружная циркуляция ү = 2 nrV ^ постоянна по пространству.

Если ось симметрии (на которой V ^ = 0) расположена внутри поля течения, то и постоянная по пространству величина окружной циркуляции ү = 2 nrV ^ должна всюду обращаться в нуль. Поэтому окружная скорость V ϕ равна нулю не только на оси, но и во всем поле течения. А это значит, что течение является незакрученным. Таким образом, приходим к следующему выводу.

Если осесимметричное течение газа потенциально и ось симметрии находится в поле течения, то такое течение лишено закрутки.

Заметим, что при осесимметричном обтекании тел вращения конечной длины можно указать часть оси симметрии, находящуюся внутри течения. Поэтому обтекание таких тел безвихревым потоком обеспечивает отсутствие закрутки. Наличие скачков уплотнения не меняет ситуацию. Действительно, в осесимметричных течениях поверхности скачков представляют собой поверхности вращения. Любая частица газа движется в составе осесимметричного кольца, являющегося фигурой вращения этой частицы вокруг оси симметрии Oz . Момент импульса этого кольца сохраняется при переходе через скачок уплотнения. Поэтому после прохождения частицей скачка уплотнения окружная циркуляция не изменится и останется равной нулю.

Итак, внешнее безвихревое закрученное обтекание тела вращения возможно, только если во всей рассматриваемой области течения ось симметрии находится внутри обтекаемого тела.

В качестве примера рассмотрим течения в осесимметричных каналах. На рис. 1 схематически изображено течение в осесимметричной области, ограниченной стенками канала, входным ( A — A ) и выходным ( C — C ' ) сечениями, а также поверхностью обтекаемого тела. Внутренность тела изображена серым цветом. Осесимметрично расположенные точки обозначены одной и той же буквой (например, точки A ).

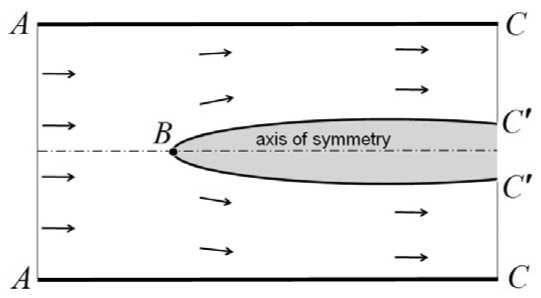
Рис. 1. Часть оси симметрии находится внутри течения

Часть оси симметрии, расположенная левее точки B , находится внутри течения, а не внутри обтекаемого тела. Поэтому при любых параметрах течения во входном и выходном сечениях и при наличии закрутки течение будет вихревым.

Подобный вывод нельзя сделать для течения в области, изображенной на рис. 2 (несмотря на то, что рис. 2 можно считать частью рис. 1). В этом случае ось симметрии целиком лежит внутри обтекаемого тела.

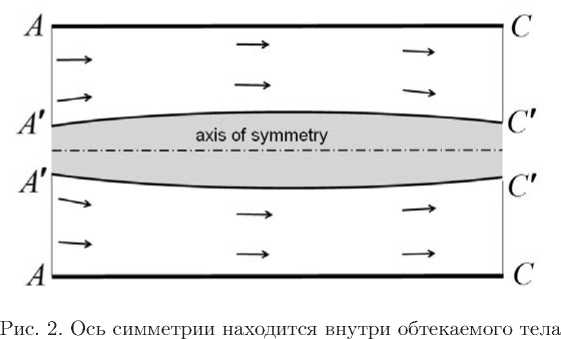
В изображенной на рис. 2 части осесимметричного канала ни одна точка течения не лежит на оси симметрии. Следовательно, полученный в данной статье результат не исключает возможности задать такие параметры течения во входном ( A — A ) и выходном ( C — C ' ) сечениях, которые могут обеспечить реализацию безвихревого обтекания с закруткой. Например, если обтекаемое тело представляет собой цилиндр радиуса r о >  0, то одним из возможных течений является так называемый потенциальный вихрь. Это стационарное течение вне цилиндра ( r > r о ), компоненты скорости которого V r = 0, V _v = C 1 / r , V _z = C 2 , где C 1 , C 2 = const.

Следует подчеркнуть, что полученное выше необходимое условие существования закрутки в потенциальном течении (ось симметрии должна быть внутри тела) не является достаточным. Как и другие необходимые, но недостаточные условия, оно может эффективно использоваться только в случаях, когда это необходимое условие нарушено. То есть для утверждения о невозможности существования закрутки в потенциальном течении. Выполнение этого необходимого условия (как, например, в ситуации, изображенной на рис. 2) еще не означает, что потенциальное течение с закруткой обязательно может быть реализовано. Обсуждение возможности реализации потенциального течения с закруткой при выполнении полученного выше необходимого условия выходит за рамки данного исследования.

4.    Эквивалентность стационарных тотально закрученных

и незакрученных течений в потенциальном поле массовых сил

В работе [2] без предположений о баротропности или адиабатичности показано, что для осесимметричных течений идеального газа окружная циркуляция ү = 2 nrV ^ сохраняется в частице газа, то есть является первым интегралом движения:

∂γ дү + (V -V) ү = 0.

В частности, для стационарных течений это означает, что окружная циркуляция ү = 2 nrV _v может быть различной на разных линиях тока, но сохраняет постоянное значение на каждой линии тока.

Тотально закрученным течением назовем течение, в котором нет точек с нулевой окружной скоростью Vϕ. Рассмотрим стационарное тотально закрученное течение в отсутствие внешних сил. В стационарном случае окружная циркуляция γ постоянна вдоль линий тока (V - V) ү = 0 и не обращается в нуль. Поэтому ее можно использовать в качестве функции преобразования Мунка–Прима [3], связывающего параметры течений газа с одинаковой картиной линий тока и идентичным распределением давления. Эта связь выражается формулами

V = Y V 1 , Р = ^ , p = p 1 .                          (7)

γ ²

Непосредственной проверкой можно убедиться, что функции нового течения (с индексом 1) удовлетворяют стационарным уравнениям Эйлера:

div( р 1 V 1 ) = 0 ,

« 1 x V 1 = -^ -v (V 2) , р 1        V ² /

Q ₁ = rotV ₁ .

Обозначим V 1 = V 1 r e _r + V 1 y e y + V 1 z e z = V 1 _r + V 1 y + V 1 z . Замена (7) подобрана таким образом, что в новом течении окружная циркуляция постоянна:

V 1 v = 2ПГ и Y 1 = 2 nrV ^L v = ¹ .

Поэтому, согласно (6),

O1 rz = - — [ev x Vy 1] = 0, и, следовательно, в силу стационарности, уравнение (4) вырождается. Оставшиеся уравнения (3), (5) для нового течения (V1 r, V1V, V1 z, p 1, р 1) в отсутствие массовых сил (П = 0), с учетом равенства V1 у = ^^r, выглядят следующим образом:

П 1 v x ( V 1 r + V 1 z ) = - ^ -V ( V r + V ² ) + ¹ (-¹- V • e r , р ₁       \ 2     2 r \2 nr

⁽ р 1 V 1 r ) ⁺ Р ^{1 1} r ⁺ — ⁽ р 1 V 1 z ) = ⁰ .

∂r           r ∂z

Эти уравнения идентичны уравнениям незакрученного течения с параметрами V 2 r = V 1 r , V 2 _v = 0 , V 2 _z = V 1 _z , p 2 = p 1 , р ₂ = р 1 в поле массовых сил с потенциалом ^П = 8 n ¹ r 2 ^:

• ^{fi 2 v x (} V ² r ⁺ V ² z ) = "^Vlp 2r ^-v ( V 2 r ⁺ V 2 z ⁺ 8 П 2 Г 2 ) ,               ⁽⁸⁾

• I" ( р 2 V 2 r ) + ^р 2^ + ^d ( р 2 V 2 z ) = 0 .                        (9)

∂r           r ∂z

Таким образом, каждому решению ( V 2 _r , V 2 v = 0 , V 2 _z , p 2 , р 2 ) какой-либо двумерной задачи незакрученного осесимметричного обтекания с потенциалом внешних массовых сил 8 Пr ₂ (уравнения (8) и (9)) соответствует семейство решений ( V, V ^ ,V _z , p, р ) задач закрученного обтекания в отсутствие внешних массовых сил:

V r = yV 2 r ,  V z = yV 2 z ,  V v = -^ ,  р = ^р 2 ,  p = p 2 ,              (10)

• 2 nr ү²

5.    Инвариант линий тока стационарных закрученных осесимметричных течений

где ү = 0 - произвольная функция постоянная вдоль линий тока. При этом каждая конкретная функция γ задает такое решение из указанного семейства, в котором величина γ является окружной циркуляцией 2 nrV _v .

Только что установленная связь удобна тем, что поверхности вращения линий тока незакрученных и тотально закрученных течений, связанных отношениями (10), совпадают. Поэтому все эти течения соответствуют обтеканию одних и тех же конфигураций. Любое тотально закрученное течение ( V y = 0) внутри выбранной пространственной конфигурации может быть получено соответствующим подбором функции γ, постоянной вдоль линий тока, по формулам (10) из незакрученного решения задачи с уравнениями (8), (9) и с «незакрученными» граничными условиями.

При отсутствии радиально-осевого движения, когда все частицы вращаются вокруг оси Oz , инвариантом линии тока является любой параметр жидкой частицы. Поэтому содержательным является исследование инвариантов при наличии радиально-осевой скорости: V r + V z = 0.

Для стационарных течений баротропного газа справедлива теорема Эйлера–Эртеля [4], которая позволяет получить инвариант линий тока с использованием другого известного инварианта. Так, например, в работе [5] с помощью теоремы Эйлера–Эртеля был получен новый инвариант течений газа. Но в рассматриваемом течении применение теоремы Эйлера–Эртеля к энтропии, к полной энтальпии и к окружной циркуляции дает тривиальный результат. В осесимметричных течениях место инвариантов, получаемых с помощью теоремы Эйлера–Эртеля, занимает другой, нетривиальный инвариант. При этом в отличие от инвариантов Эйлера–Эртеля не предполагается баротропность или адиабатичность течения.

В стационарном случае при условии V r + V z = 0 из формулы (4) следует существование скалярного поля λ , такого, что

А ( V r + V z ) = Q rz .

Применение оператора дивергенции к этому уравнению дает

А div ( V r + V z ) + ( V r + V z ) VA = 0 .

С другой стороны, из уравнения неразрывности следует, что p div (Vr + Vz) + (Vr + Vz) Vp = 0.

Следовательно,

( V r + V z ) V A = 0 ,

( V r + V z ) V    ’^Q rz ¹    =0 .                            (11)

p I V r + V z I

Поэтому отношение _{ρ| V} ^{| Ω} _{r +} ^rz _V ^| _{z |} постоянно вдоль линий тока.

Подчеркнем, что формула (11) получена без предположений о баротропности или адиабатичности течения. Более того, при ее выводе не использовалось уравнение импульсов (1), а только уравнение неразрывности (2). Поэтому формула (11) остается верной и для стационарных осесимметричных течений вязкого газа.

Заметим, что в винтовых течениях (в которых завихренность параллельна скорости) величина _{ρ| V} ^{| Ω} _{r +} ^rz _V ^| _{z |} также является инвариантом вследствие инвариантности для винтовых течений величины _ρ ^| _| ^Ω _V ^| _| [4]. Действительно, поскольку в винтовых течениях завихренность параллельна скорости, отношение длины вектора Ω к длине вектора V равно отношению длин проекций этих векторов на меридиональную плоскость, то есть - отношению | Q _rz | к I V _r + V _z | . При этом формула (11) верна как для винтовых течений, так и для течений общего вида. Поэтому она представляет собой самостоятельный новый результат наряду с уже известными для осесимметричных течений вязкой жидкости [6, 7].

6.    Заключение

Проведен анализ полных уравнений Эйлера осесимметричного закрученного течения идеального газа, которое в общем случае может быть вихревым, а энтропия может быть различной на разных линиях тока. Получен ряд новых, неизвестных ранее свойств таких течений.

Результаты могут быть применены для качественного анализа течений, а полученный новый инвариант (11) – для верификации численных расчетов при отладке расчетных комплексов.