О некоторых вопросах динамики тангенциального привода для крутильного органа пневмомеханической прядильной машины

Для различных режимов работы прядильного устройства процесс разгона крутильного органа должен выполняться в различное время [1].

У тангенциального привода (рис. 1, а и 1,б) по сравнению с индивидуальным тесемочным приводом условия разгона для первого и последнего по ходу ремня крутильных органов различны из-за изменения натяжения ремня вдоль его контура.

С целью определения зависимости натяжения ремня от необходимого времени разгона крутильного органа решим дифференциальное уравнение движения крутильного органа в приводе по схеме рис. 1, а:

‘ к^=мд - М с ⁽¹⁾

Где ‘_k -момент инерции крутильного органа;

ш_к -угловая частота вращения крутильного органа;

t - время разгона крутильного органа;

М д - движуший момент;

М_с -момент сопротивления крутильного органа.

Движущий момент М д - найдем по выражению:

М д = Р_к- Г_к (2)

Где Р к -усилие, прилагаемое к шкиву крутилного органа.

Г к -радиус шкива крутильного органа.

Направляющий ролик

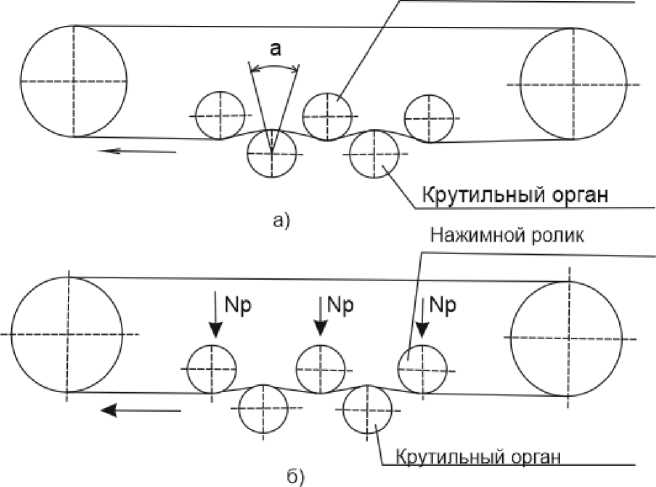
Рис 1.Схемы тангенциального привода: а-вариант с неподвижными направляющими роликами; б-вариант с подпружиненными нажимными роликами.

Величину Р_к можно представить как разницу натяжения ремня на шкиве крутильного органа, т.е.

Р_к = Т₁-Т₂ = T₂e^af-T₂ = Т₂(е^а ' - 1) = Т₂(е^м ' - 1), (3)

Где Т 1 -натяжение сбегающей ветви ремня;

Т₂- натяжение набегающей ветви ремня;

е-основание натруальных логарифмов;

a-угол обхвата ремнем шкива;

/-коэффициент трения ремня по шкиву;

a-коэффициент пропорциональности.

Момент сопротивления  Мс   крутильного органа получен экспериментальным путем и представляется в зависимости от времени разгона до номинальной частоты вращения крутильного органа выражением.

М_с = М ' + М ‘ -М ' + М ‘ + bt² (4)

Где М -постоянная часть момента сопротивления;

М -часть момента сопротивления нарастаюшая с увеличением частоты вращения;

b-коэффициент пропорциальности;

t -время разгона крутильного органа до номинальной частоты вращения.

После интегрирования натяжения набегающей ветви органа t, т.е.

уровнения (1) получаем зависимость ремня Т2 и времени разгона крутильного

■■

Т2

Y^-(eaf-a f-1) *к

Подобная задача решена и для схемқ привода (рис.1,б) крутильного органа, в которой угол обхвата а ремнем шкива не является постоянном, а соблюдаются условия прижима ремня к шкиву крутильного органа с постянной силой.

Время разгона,с. Величина, кгс	0.1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
Т 2	152	77	52	39	32	26,9	23,2	20,4	18,5	16,7
рк	7,8	3,94	2,67	2,0	1,64	1,37	1,19	1,05	0,95	0,85
F(N p ,W	7,9	4,0	2,7	2,05	1,65	1,39	1,21	1,07	0,96	0,87

Проинтегрируем для такого исполнения привода дифференциальное уравнение движения крутильного органа.

^^(А^-Ъ-Мс (6)

Где  F(Np, t)f-окружное усилие, прикладываемое к шкиву крутильного органа;

F(N p , t)-функция определяющая силу нормального давления ремня на поверхность шкива крутильного органа, зависящая от времени разгона крутильного органа.

После получаем:

z s   2^+М' X)

F(N p , t)f = ——- (7)

В табл. 1 приведены значения подсчитанных величин натяжения набегающей ветви ремня в зависимости от времени разгона крутильного органа, окружного усилия на шкиве крутильного органа для обеих упомянутых схем привода.

Рассчет выполнен для частоты вращения крутильного органа в 15000 об/мин с углом обхвата а = 10 и коэффициентом трения ремня по шкиву f = 0,286.

На рис.2 приведены графически величины расчетного натяжения набегающей ветви ремня в зависимости от времени разгона крутильного органа для различных значений угла обхвата а , коэффициента трения f. Расчет выполнен на ЭВМ. При этом коэффициент трения, как показано в работе [2], принят при значительном скольжении ремня неизменяющимся.

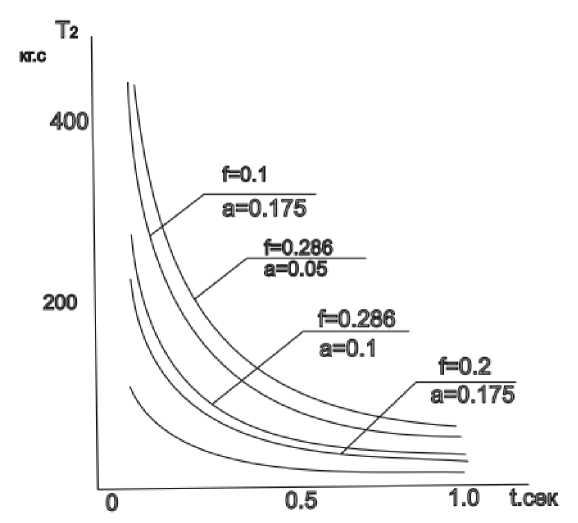
Рис.2. Зависимость натяжения набегающей ветви ремня от времени разгона крутильного органа.

По экспериментальным данным [3], окружное усилие на шкиве крутильного органа при номинальной частоте вращения 15000 об/мин равно ~0,073 кгс. Следовательно, на сторонку машины в 75 крутильных органов суммарное усилие на шкивах должно быть порядка 6 кгс. Если потребуется такое же усилие для вращения направляющих роликов то суммарная разность натяжения ремня в крайних точках возрастет до 10-12 кгс. Такая разность при минимальном натяжении ремня будет сопровождаться изменением времени разгона крутильного органа от 1,0 до 0,6 с, т.е. почти вдвое (см.табл.1). Это будет вызывать и соответствующие изменения условий ликвидации обрыва пряжи [1], так как процесс разгона крутильного органа тесно связан с процессом наполнения прядильного устройства волокнами, длительность которого для указанных условий должна быть в пределах 0,14^0,17 с [1]. Если начинать одновременно подачу волокон и разгон крутильного органа, то в конце заполнения прядильного устройства волокнами крутильный орган не будет иметь надлежащей частоты вращения. Увеличения натяжения ремня может уменьшить эту несогласованность, но чтобы довести время разгона крутильного органа дл 0,14^0,17 с, нужно натянуть ремень до 60^70 кгс. Это нецелосообразно, так как долговечность привода будеть неудовлетворительной.

Привод с пружинным поджатием направляющих роликов до усилия на шкиве крутильного органа ~ 2,5 кгс можеть разогнать крутильный орган в течение 0,9^ 1,0 с (см. табл. 1), что также не обеспечивает условий ликвидации обрыва пряжи.

Поэтому потребуются такие действия оператора, которые позволят сначала начинать разгон крутильного органа, а потом через определенные отрезки времени включать подачу волокон в прядильное устройство и вывод пряжи из него.

Выводы

• 1 .Теоретически найдена зависимость необходимого натяжения набегающей ветви ремня в тангенциальном прводе крутильных органов от времени разгона крутильных органов.

• 2 .Даже в случае идентичного выполнения приемов ликвидации обрывов пряжи будет различаться на крайних прядильных местах одной стронки машины.

• 3 .Одним из условий возобновления процесса прядения при ликвидации обрыва пряжи на машине R-60 с тангенциальным приводом является необходимость опережения включения в работу крутильного органа по сравнению с началом подачи волокна в прядильное устройство.