О нелинейной динамике квази-хрупкого разрушения (экспериментальное и теоретическое исследование)

Nonlinear dynamics ofcrack propagation is the subject of the growing interest during last decade due to the experimental observation of dynamic stochasticity effects and tire discovery of the crack behavior that is in the strong contradiction with the traditional view in the fracture mechanics. Experiments showed the existence of the limited velocity E, ~ (t4i ’. (V_R is the Rayleigh wave speed) for the steady-state crack propagation and the threshold character of the transition to the branching regime with the stochastic dynamic^. The established experimental data revealed some unresolved puzzles from point of view of tire traditional crack mechanics. The main question is concerning the nature of physical mechanisms controlling the crack dynamics including the branching, stochastic dynamics and the crack arrest. Explanation of the limiting steady-stale crack velocity and the transition to the branching regime was proposed by authors due to the experimental and theoretical suidy of the collective behavior in the microcracks ensemble at the crack tip area.

Нелинейная динамика разрушения вызывает нарастающий интерес в течение последнего десятилетия вследствие появления новых экспериментальных данных, обнаруживших несоответствие поведения трещин с предсказаниями классической теории. Эксперименты показали существование предельных скоростей устойчивого прямолинейного распространения трещин И ~0,41_А (14 - скорость волны. Редея) и пороговый характер перехода к режиму ветвления с последующей стохастической динамикой [1-3]. Представляется проблематичным объяснение указанных эффекiив в рамках традиционной механики трещин [4], и актуальным остается вопрос с природе физических механизмов, контролирующих распространение трещин, включая ветвление, стохастическую динамиту. остановку трещин, а также условия самоподдерживаюшегося разрушения, так называемых волн разрзшешы. Теоретическое объяснение существования предельных скоростей прямолинейною распространения и перехода к режиму ветвления предложено в [5] на основе коллективных эффектов в ансамбле дефектов (микротрещин) в окрестности вершины трещины.

Феномен "волн разрушения" в квази-хрупких материалах является предметом интенсивного изучения на протяжении последних двух десятилетий. Этот термин был введен в [6] как предельный случай эволюции поврежденное! и, кота ансати.ш микросдвигов (в зоне сжатия) формирует фронт, распространяющийся с некоторой групповой скоростью. Этот фронт отделяет дисперсно-разрушенный объем от структурированного материала.

Статистические свойства ансамбля дефектовМикроскопические и макроскопические параметры поврежденности

Структурные параметры, ассоциированные с типичными мезоскопическими дефектами (микротрещинами, микросдвигами), были введены в [7] с использованием дислокационных представлений. Эти дефекты описываются симметричными тензорами вида s_ik = худ'_к в случае микротрещин и s_ik -1/2д(у4 + /,v_t) Д^ля микросдвигов. Здесь v - единичный вектор нормали к основанию микротрещины или площадки сдвига: 1 - единичный вектор в направлении сдвига; s - объем микротрещины или интенсивность сдвига для тензора микроскопического сдвига. Усреднение "микроскопического" тензора s_ik дает макроскопический тензор плотности микротрещин (микросдвигов) p_ik = n(s„), совпадающий с деформацией, обусловленной дефектами, о концентрация дефектов.

Статистическая модель упругой среды с дефектами

Статистические свойства ансамбля дефектов были исследованы на основе решения уравнения Фоккера - Планка [8,9] в фазовом пространстве возможных состояний, v, 1 и 5 микроскопических переменных 5_Й. Это решение позволило определить вид потенциала (свободную энергию F\ обусловленного дефектами (рис.1).

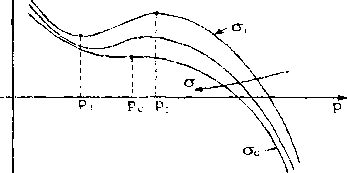
Рис.1. Зависимости свободной энергии F от параметра плотности дефектов р с увеличением напряжения о

Метастабильность для интервала напряжений G < с> является следствием ориентационного взаимодействия между дефектами. Вид свободной энергии, предсказанный статистической моделью, приближается к виду Гриффитса для ст ><7, (см. рис. I), что соответствует инициированию и росту дефектов, ориентированных по полю напряжений.

О феноменологии квази-хрупкого разрушенияСвободная энергия

Феноменологическое представление части свободной энергии, обусловленной дефектами (для случая одноосного растяжения р = р_:-. о = о„, е = е„), может быть получено на основе разложения (по аналогии с подходом Гинзбурга - Ландау в теории фазовых переходов) до шестого порядка по тензору плотности дефектов [8].

F — у^Арг-У^Вр4 - у^Ср6 - Do р + У^7!Р

Градиентный член в (1) описывает "нелокальные" взаимодействия в ансамбле дефектов, А, В, С, D - коэффициенты разложения, % - параметр нелокальное™.

Кинетика поврежденности при квази-хрупком разрушении

Кинетика накопления повреждений при квази-хрупком разрушении

определяется условием эволюции системы, имеющей единственный канал диссипации

энергии - накопление и рост' повреждений:

SF/ /5г

3(...у

/ 5д

символ

вариационной производной. Линейная связь между термодинамическими потоком сйлой приводит к уравнению движения для параметра плотности дефектов

^— = -Г\Ар - Вр3 - Ср3 - Da - ~(х^~-)L           । dt                                                  ' дх; ;

где Г - положительный кинетический коэффициент. Уравнение движения (2) и соотношение для полной деформации Е -С а + р (С - компонента тензора упругой податливости) представляют собой систему определяющих уравнений для квазихрупких материалов с дефектами рассматриваемого типа.

Коллективные свойства ансамбля дефект ов

Автомодельное решение

Уравнение (4) описывает характерные стадии эволюции поврежденности. В диапазоне напряжений а < а, и параметра плотности дефектов р<р_с кинетика поврежденности "подчиняется термодинамической ветви", определяющей локальные минимумы свободной энергии (см. рис. 1).

При стремлении напряжения к критическому значению а, ( р —> р ) уравнение движения (2) качественно изменяет свой тип (от эллиптического к параболическом) ) и кинетика поврежденности подчиняется эволюции пространственно-временных структур специального вида, появление которых обусловлено взаимодействием между дефектами. Эти структуры описывают локализацию разрушения, предшествующую зарождению очагов макроскопических трещин. Е? предположении для термодинамической силы и коэффициента нелокальное™ степенных зависимое гей dpPjp ^ S.p. p vp “, Х~Хо(рЛр^ пРи переходе через критическую гонку ру, кинетическое уравнение для р может быть записано в виде dt              ах\          dx )

Зарождение локализованных пространственно-временных структур описывается автомодельными решениями уравнения (3), которые имеют вид р^ = 8^Ш^ЛНьД<У g^ = G^r"-     (4)

Здесь G>0, m>0 - постоянные параметры; L_c(0 ^и ^ " параметры скейлинга, которые могут быть найдены при решении соответствующей нелинейной задачи на собственные значения [10]. Автомодельное решение (4) описывает взрывообразную кинетику роста дефектов в виде так называемых диссипативных структур обострения на спектре пространственных масштабов L_H=kL_c(t\ к = \,2,...К при f —> т_г. Исчезновение метастабильности при О'—> ст,. (см. рис. 1) приводит к качественным изменениям в поведении системы, включая изменение ее симметрийных свойств. В области а > о., поле напряжений не контролирует поведение системы, и сценарий разрушения определяется развитием и взаимодействием локализованных структур обострения в окрестности вершины трещины, так называемой зоне процесса (the process zone).

Закон движения фронта локализованных структур определяется собственными значениями нелинейной автомодельной задачи £г и видом профиля /(£):

ь 1/2 с2(Р-1)

.                                   (5)

Уравнение (5) определяет характерные режимы локализации разрушения на спектре фиксированных масштабов при р = ^-1 и при распространении очагов разрушения

О природе неустойчивости вершины трещины

Зарождение макроскопических очагов разрушения происходит на масштабе L- за время т_с развития автомодельного профиля ptxJY Критическая скорость 1< перехода от устойчивого (steady-state) к неустойчивому (branching) режиму распространения трещины определяется очевидным условием У_с = L_cjt_i . Устойчивый режим распространения реализуется в случае, когда темп нарастания напряжений в "зоне процесса" обеспечивает время разрушения /, >г, =^^ , необходимое для формирования хотя бы одного очага разрушения в направлении основной трещины. Время разрушения t_f следует из уравнения (2) и представляет собой сумму времени "индукции" г, (времени формирования профиля p^x,G на масштабе L_H , близкого к автомодельному), и времени обострения 1/. t_f = Z_i+/_r. Для скоростей К < К. время индукции t, » t, и дочерние трещины возникают только в направлении максимальных растягивающих напряжений, т.е. в направлении основной трещины. Для скоростей

Р = И_Г должен наблюдаться переходный режим ^"Vb сопровождающийся зарождением множественных очагов в направлении ориентации основной трещины. Рост скорости трещины (Н>Н₍) ведет к резкому уменьшению времени индукции tj — > О, I, -^t. и сопровождается расширением зоны процесса в продольном и поперечном направлениях, зарождением в ней множественных очагов разрушения, и. как следствие, выраженным ветвлением основной трещины при слиянии с этими очагами.

Экспериментальное изучение нелинейной динамики трещиныСхема эксперимента

Экспериментальное исследование динамики трешины проводилось на предварительно нагруженном (фиксированное удлинение) плоском прямоугольном образце из ПММА с использованием высокоскоростной записывающей камеры Remix REM 100-8 (время задержки между кадрами 10 мкс), сопряженной с поляризационно-оптической установкой (рис, 2) [11].

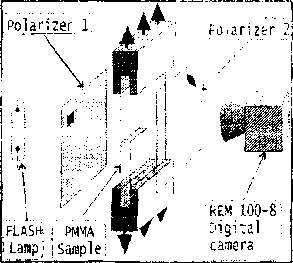
Рис. 2. Схема эксперимента

Рис.З. Характерные режимы динамики трещины

Эксперимент обнаружил что переход через критическую скорость Г? сопровождается появлением волновой картины напряжений, генерируемых в зоне процесса (рис.З). Независимые оценки скорости зрещины но прямой рлимрацит координаты её вершины и допплеровскому искажению волновых картин показали соответствие данных результатам Fineberg [1] (Fc = 0,4^ )■

Характеристические скорости распространения трещин

Зависимость скорости распространения трещины от величины начального растягивающего напряжения приведена на рис. 4. Три характерных участка и соответствующие им скорости могут быть выделены на этих зависимостях: скорость перехода от устойчивого к немонотонному прямолинейному распространению Fs =220 м/с; критическая скорость перехода к началу режима ветвления

V_c =330 м/с; скорость перехода к режиму ветвления при автономном развитии ветвей.

Оценка размера зеркальных зон (зон локализации разрушения) L_c = 0,3 мм при характерной скорости V_c =330 м/с перехода к ветвлению позволяет определить время обострения t,; г_с=^с/ = М0'⁶ с. Близкая оценка t_c получена в [7] при ударноволновом разрушении ПММА в области "динамической ветви".

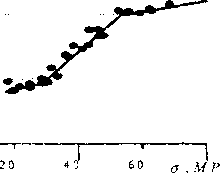
Рис.4. Зависимость характерных скоростей трещины от напряжения

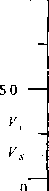
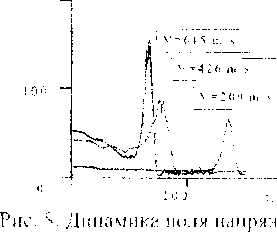
Рис. 5. Зависимость плотности зеркальных зон для характерных скоростей трещины

В экспериментах также были установлены корреляции между характерными скоростными режимами распространения трещин (рис. 4) и плотностью (средним размером) зеркальных зон на поверхности разрушения (рис. 5). Время разрушения при F > И_с практически постоянно (Гу =Z_C = I мкс), поэтому единственной возможностью увеличения скорости трещины является увеличение размеров зоны процесса. Таким образом, скорость трещины Г определяется отношением размера зоны процесса L_pz ~ L_H и времени обострения t_c: V = ^ у^ • Поскольку масштаб ветвления трещины определяется размером зоны процесса, из последнего соотношения следует линейная зависимость характерной длины ветвей от скорости трещины. Этот результат объясняет резкую зависимость (квадратичный закон) энергии диссипации от скорости трещины, установленный в [12].

Скейлинг в процессе разрушения

Свойства скейлинга в процессах разрушения изучались в рамках вышеописанной экспериментальной схемы при записи динамики поля напряжений с использованием лазера и поляризационной системы. Динамика поля напряжений определялась в точке, расположенной на расстоянии 4 мм от траектории прямолинейного распространения трещины, что позволило нам построить сечение Пуанкаре в переменных о~ о для случая медленных и быстрых трещин (рис. 6).

д,МРи! ^is

О". МРа¹US

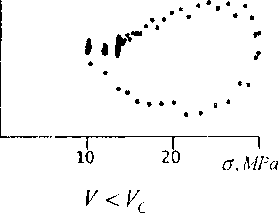
Рис. 6. Сечение Пуанкаре в переменных о - о

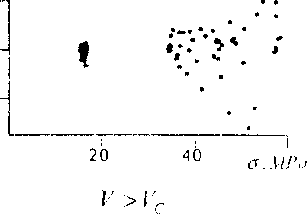
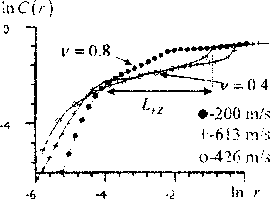
Рис. 7. Корреляционный интеграл

Фазовые портреты на рис.5, б отражают периодическую динамику поля напряжений для V с, что находится в соответствии с локальной эллиптичностью уравнения (2) для OC, и стохастическую динамику для V :>У,., соответствуют;, ю второму типу аттрактора. Запись динамики напряжений в указанной точке при Г' >г обнаружила появление конечно-амплитудных флуктуаций поля напряжений, которые отражают появление качественно новых процессов в зоне процесса для быстрых трещин (рис.8). Изменение скейлинговых и, как следствие, симметрийных свойств системы показано на рис. 7, где представлены значения корреляционно! о интеграла С(г), вычисленного по временным экспериментальным последовательностям напряжений. Было установлено наличие масштабов с постоянными значениями корреляционных индексов для К<К.. (Г = 200 м/с, v = 0,8) и 1 > Г >Г₍ (Р'=426, 613 м/с, у = 0,4). Эти значения корреляционных индексов свидетельствуют о существовании двух режимов с детерминистической и стохастической .динамикой.

Изменение протяженности областей на зависимостях корреляционного интеграла С( г) с постоянными значениями корреляционных индексов качественно соответствуют изменению размера зоны процесса L_ra . Размер этих зон растет с ростом скорости в диапазоне Г, > Г >И_С с сохранением свойств скейлинга для динамической системы. Численное исследование кинетики накопления дефектов в зоне процесса позволило нам прийти к заключению, что изменение скейлинга связано с подчинением динамики системы новому спектру независимых переменных, соответствующих спектре пространственно-локализованных структур с взрывной кинетикой когерентного роста дефектов [11].

Резонансное возбуждение разрушения. Волны разрушения

Волны разрушения возникают в ударно-нагруженных материалах (стеклах, керамиках) как специфическая запаздывающая мода разрушения, в которой материал полностью теряет прочность после прохождения волны напряжений [13, 14]. Традиционно феномен "волн разрушения" рассматривается в контексте известных и до настоящего времени открытых проблем в описании механическою поведения ударно-нагруженных материалов: динамическая прочность, пределы упругости Гюгонио, релаксация упругого предвестника. Важным признаком волн разрушения является независимость их скорости от скорости распространения единичных трещин. Уровень запасенной упругой энергии в материале является основным фактором, обеспечивающим самоподдерживающийся режим распространения разрушения. Квази-хрупкие материалы обнаруживают очень высокую динамическую прочность на сжатие, высокий предел упругости Гюгонио и, как следствие, способность запаса высокого уровня упругой энергии при прохождении ударной волны.

Моделирование волн разрушения

Моделирование зарождения и распространения волн разрушения проведено в [15] на основе определяющих уравнений (2), дополненных уравнениями сохранения импульса.

Рис. 9. Распространение волн напряжения (S) и волн разрушения (F)

Моделирование подтвердило независимое (от волны напряжений) распространение волны разрушения (рис. 9). сопровождающееся исчезновением сдвиговой компоненты тензора напряжений. Уровень поперечных напряжений в этом случае приближается к значениям продольных напряжений (рис. 10), что подтверждается прямыми измерениями состояния материала за фронтом волны разрушения.

Рис. 10. Динамика продольных ог. и поперечных о,,, напряжений