О нелинейности электрокинетических явлений. Обзор

ВВЕДЕНИЕ. ФОРМУЛИРОВАНИЕ ПРОБЛЕМЫ

В электрохимии традиционно при изучении электрокинетических явлений (ЭКЯ) (электроосмос, электрофорез и обратные к ним потенциал течения (эффект Квинке) и потенциал седиментации (эффект Дорна)) при изучении формальной связи между характерными скоростями движения в этих явлениях U и амплитудой напряженности стороннего электрического поля E используется линейное приближение U ~ f ( Г ) E * . Здесь Г характеризует параметры рассматриваемых элек-трокинетических процессов. Такое приближение справедливо лишь в слабых электрических полях E = |E|. Именно так описаны электрокинетические процессы в известных публикациях [2–5] и др., и область ЭКЯ, где это справедливо, уместно назвать областью линейных, или классических, ЭКЯ. При больших величинах E это приближение может стать неприемлемым вследствие нарушения линейной зависимости U ~ F ( E ) . Это может быть следствием как нарушения линейности этой зависимости, так и изменения физики самого электрокинетического процесса по мере роста величины E .

Задачей настоящей работы является обзор известных на настоящий момент методов решения нелинейных задач динамики в условиях нелинейных ЭКЯ.

ОБЗОР МЕТОДОВ РЕШЕНИЯ НЕЛИНЕЙНЫХ ЗАДАЧ ЭКЯ

Нелинейности, связанные с пондеромоторной силой

В основе математического формализма при получении зависимости U ~ F ( E ) лежит выбор замкнутой системы уравнений электрогидродинамики (см., например, [6–11]), в которую, в частности, входит уравнение Навье—Стокса движения жидкости

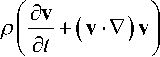
= -V p + n A v + f .

Уравнение (1) есть уравнение сохранения импульса для несжимаемой жидкости с динамической вязкостью η , с плотностью ρ , скоростью течения v и давлением в жидкости p . В правой части (1) фигурирует т.н. пондеромоторная сила f , которая в жидкостях обычно представляется в виде выражения Гельмгольца [12, с. 95]

f = p E - EV + ^0- V^f E ² p^Ъ. ) .    (2)

e 2         2  (    d p J _T

Здесь ρ _e E — сила Кулона, с которой действует электрическое поле E на имеющиеся в жидкости заряды с объемной плотностью (заряд единицы объема жидкости) ρ _e ; второй член — сила, прикладываемая к жидкости при наличии неоднородности электрического поля ( s ^ const), и третий член (потенциальный) называется стрикционным давлением и может объединяться с гидродинамическим давлением; ε ₀ — электрическая постоянная; ε — относительная диэлектрическая проницаемость жидкости; T — абсолютная температура жидкости. В традиционной электрокинетике величина объемной плотности заряда принимается независимой от величины стороннего электрического поля.

Первый член выражения для пондеромоторной силы — сила Кулона ρ _e E — обычно доминирует, особенно при наличии постоянного электрического поля E в проводящих жидких диэлектриках. Второй член — сила, прикладываемая к жидкости при наличии неоднородности электрического поля. Обычно она меньше силы Кулона и может доминировать при приложении переменного электрического поля к изолятору. Третий (потенциальный) член называется стрикционным давлением и может объединяться с гидродинамическим давлением [7, с. 124]. Как было показано в [10], при подаче наряду с постоянным электрическим полем и переменного электрического поля при существенной величине второго и третьего членов в (2) могут возникать кратные (паразитные) гармоники колебаний. Это и может являться критерием существенности величины второго и третьего членов в (2).

Таким образом, при использовании модели (1), (2) в этих уравнениях может возникать нелинейность по электрическому полю до порядка |f| ~ O ( E ² ) . При этом плотность заряда p e полагалась независимой от величины E . На практике, впрочем, обычно обходятся линейной зависимостью пондеромоторной силы [2–5 и др.]

f ” P e E . (3)

Нелинейности, связанные с поляризацией двойного электрического слоя

Сравнительно недавно появились работы, в которых теоретически было предсказано и подтверждено на практике наличие зависимости плотности заряда ρ _e от величины напряженности электрического поля применительно к электрокинети-ческим задачам (см., например, оригинальные и обзорные работы [13–20]). Такого сорта задачи были отнесены к нелинейной электрокинетике.

Так, в работе [3] гл. 10 посвящена рассмотрению нелинейных электрокинетических явлений. Там, в частности, отмечается [3, с. 195], что общей чертой всех существующих теорий поляризации двойного слоя является учет только линейных по полю эффектов, поэтому имеющиеся формулы зависимости скоростей справедливы лишь в слабых полях.

За время, прошедшее после выхода работы [3], произошел существенный прогресс в этом направлении. Так, например, в работах [13–15] рассматривается электроосмос с индуцированным зарядом. Речь идет о том, что в результате поляризации двойного слоя на границе раздела (твердое тело—жидкость) в сильном электрическом поле нарушается линейная зависимость U ~ F ( E ) , характерная для слабых полей. Происходит это потому, что в сильных полях электроки-нетический потенциал перестает быть независимым от амплитуды внешнего поля E и становится от него линейно зависимым

Z - E . (4)

Как следствие меняется линейная зависимость U ~ E для слабых полей на квадратичную зависимость

U - E 2 , (5)

т.е. лишняя степень E возникает за счет линейного роста величины электрокинетического потенциала от этой величины.

В работе [16] рассматриваются два вида нелинейного электрофореза, которые можно обнаружить в сильных электрических полях (несколько сотен В/см). Первый ("классический" нелинейный электрофорез) обусловлен взаимодействием внешнего поля с индуцированными полем ионными зарядами в двойном электрическом слое в условиях, когда вызванные полем изменения концентрации электролита остаются небольшими по сравнению с его равновесными значениями (т.е. в отсутствие внешнего электрического поля). В этом случае зависимость скорости U _eph классического нелинейного электрофореза определяется выражением²

U eph = M eph E + ^ .. E ³. (6)

Здесь µeph — подвижность частицы при линейном электрофорезе, когда нелинейность еще не учиты- вается; µeph-3 — подвижность, соответствующая третей степени амплитуды внешнего поля E3 ; µeph-3 от поля E не зависит, выражения для µeph-3 приведены в [16] (выражения [16, (5) и (5а)] для различных случаев).

Второй, так называемый "сверхбыстрый электрофорез" связан с взаимодействием сильного внешнего поля с вторичным диффузным слоем противоионов, который индуцируется вне первичного (классического) диффузного слоя самим внешним полем вследствие концентрационной поляризации. "Сверхбыстрый электрофорез" предсказывает квадратичную зависимость скорости электрофореза однополярных (ионных или электронных) проводящих частиц от градиента внешнего поля и линейную зависимость от размера частиц в сильных электрических полях. Это резко контрастирует с законами классического электрофореза. Выражение для скорости электрофореза проводящих частиц ионного типа определяется квадратичной зависимостью от поля E

^U eph

16 εε ₀ a

27 η

E ².

Здесь a — радиус частицы.

Электрофоретическую скорость частиц с электронной проводимостью можно приблизительно оценить [16, выражение (7)]

U ~ 4_ ss 0 ( 2 E -Ф d ) ²

eph 27 ηa

.

Здесь Фd — напряжение разложения электролита.

Скорость электрофореза в случае существования пространственного заряда с обеих сторон частицы (это справедливо для проводящих частиц электронного типа) также приведена в [16, выражение (8)]. В этом случае также сохраняется отмеченная квадратичная зависимость U eph ~ E ².

ВЫВОДЫ

В результате проведенного короткого обзора можно сделать следующие выводы.

Использование электрокинетических эффектов при значительных величинах напряженности внешнего электрического поля может значительно поднять электроосмотическую и электрофоретическую скорости, которые меняются с ростом напряженности стороннего электрического поля согласно зависимостям: U ~ E для линейных электрокинетических явлений; U ~ E3 для умеренных значений величин E , но таких, что элек-трокинетические явления уже перестают быть линейными; U ~ E2 — для больших значений величины E . Учет этих обстоятельств позволяет получать повышенные электрофоретические и электроосмотические скорости жидкости и существенно увеличивать соответствующие подвижности.

Работа выполнена в ИАП РАН в рамках Государственного задания 075-00780-19-02 по теме № 0074-20190013 Министерства науки и высшего образования.