О непараметрических алгоритмах идентификации нелинейных динамических систем

Развитие теории и методов математического моделирования нелинейных динамических систем является актуальной проблемой современной прикладной математики. Наиболее важным с практической точки зрения классом динамических процессов являются системы, допускающие активный эксперимент при отсутствии полной априорной информации о структуре и параметрах моделируемого объекта.

Постановка задачи идентификации систем. В общем виде задача идентификации нелинейной динамической системы может быть представлена следующим образом (рис. 1).

Доступная априорная информация представляет собой неравномерную выборку {ut, xi, i = 1,5} измерений входных и выходных переменных объекта объемом 5. Данные о структуре объекта отсутствуют. Требуется по наблюдаемым входным-выходным переменным процесса построить математическую модель стохастического объекта, адекватно описывающую его поведение при произвольном входном воз- действии и наличии аддитивной помехи на выходные данные.

Непараметрические модели. Основная особенность нелинейных динамических систем заключается в том, что они обладают нелинейными и динамическими свойствами, которые невозможно четко разделить. Описание нелинейной динамической системы в форме линейного передаточного коэффициента (по аналогии с линейной системой) приводит к бесконечному многообразию передаточных функций Н(jw ), так как каждой реализации входного воздействия u ( t ) и отклика x ( t ) будет соответствовать своя функция Н(jw ) [1].

Для упрощения моделирования нелинейный объект может быть представлен в виде некоторой комбинации линейных динамических и безынерционных нелинейных блоков. В таком случае модель, которая описывает исследуемый объект с требуемой точностью, представляет собой наилучшую комбинацию линейных (ЛЭ) и нелинейных элементов (НЭ) и их параметров.

Рис. 1. Общая схема идентификации:

Объект - нелинейный динамический объект; £( t ) - ненаблюдаемое случайное воздействие;

u ( t ) - входные переменные объекта; х ( t ) - выходные переменные объекта, u j , х ^ - соответствующие наблюдения переменных процесса, далее обозначаемые { u , , х , , t = 1, 5 }; s ^u ( t ), s ^х ( t ) - случайные факторы, действующие в каналах измерения переменных в дискретные моменты времени t , такие что M { s } = 0, O ' s } < да ; х ( t ) - выход модели объекта

Модель Гаммерштейна

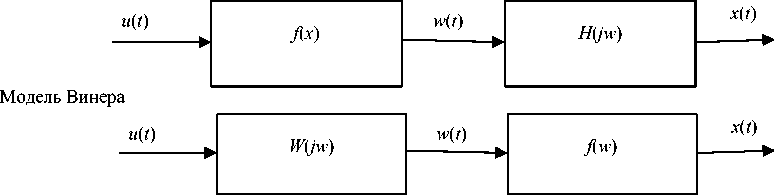
Рис. 2. Модели Винера и Гаммерштейна (обозначения см. в тексте)

Простейшие модели нелинейного динамического объекта - модели Винера и Гаммерштейна - представляют собой последовательное соединение двух блоков (рис. 2).

Преимуществом использования таких моделей является их относительная простота, выражающаяся в том, что нелинейные и динамические свойства исследуемого объекта в них искусственно разделены и сосредоточены во входном и выходном блоках. Линейный динамический блок простейшей модели должен в какой-то мере воспроизводить динамические свойства исследуемого объекта, а нелинейный блок - имитировать нелинейные свойства исследуемого объекта [1]. Однако простейшие модели описывают реальный объект лишь приближенно. Основная сложность в построении моделей таких объектов заключается в том, что внутренние сигналы w ( t ) являются недоступными для измерения.

Пусть исследуемая нелинейная динамическая система представлена в виде двух последовательно включенных звеньев - линейного динамического и нелинейного статического (модель Винера или Гаммерштейна) - и имеется выборка измерений реакции объекта на тестовое входное воздействие u ( t ): { u ( t, ) , x i } , i = 1, 5 . Данные о структуре объекта отсутствуют. Существует возможность проведения экспериментов.

Здесь возможны два случая:

• 1)    структура и параметры линейной динамической части системы неизвестны. Предположим некоторый вид нелинейности в объекте - известный с точностью до набора параметров. Тогда нелинейный элемент может представлять собой одно из следующих звеньев:

• -    квадратор, который задан соотношением

x ( t ) = a ( w ( t ) ) ²;                        ⁽¹⁾

• -    звено насыщения с порогом насыщения b 1 :

w ( t ) , x 1 ( t ) ^ b 1 ,

x (t ) = < b, w (t )> b,                           (2)

E b, w (t) < - b;

• 2)    тип нелинейного элемента неизвестен.

На основании имеющейся информации необходимо построить модель данной системы, адекватно описывающую ее поведение.

Задача идентификации нелинейной системы может быть разделена на две части: идентификацию линейного элемента и идентификацию нелинейной системы.

Рассмотрим задачу идентификации линейного элемента.

Метод построения непараметрической модели линейной динамической системы (ЛДС) основан на том, что реакция такой системы w ( t ) на входное воздействие u ( t ) описывается интегралом Дюамеля (сверткой) [2]:

t x (t) = k (0) u (t) + J k'(t - t) u (t) d т =

t

• = k (0) u ( t ) + J h ( t — t ) u ( t ) d t ,               (3)

где k ( t ) - переходная функция системы; т - переменная интегрирования; h ( t ) - весовая функция системы.

Для вычисления значения выхода объекта x ( t ) необходимо знать его весовую функцию h ( t ) . Однако на практике снятие весовой функции с объекта представляется невозможным. Поэтому основная идея идентификации ЛДС в условиях непараметрической неопределенности состоит в непараметрическом оценивании весовой функции.

Запишем оценку переходной функцию системы в виде стохастической аппроксимации регрессии непараметрического типа следующим образом:

5                (1

k = Ek ■ H t-i , si

• 5 ■ C i = 1        I C J

  
  

где ki - реально снятые значения переходной характеристики ЛДС, т. е. сигнал, получаемый на выходе системы при подаче на ее вход единичного ступенчатого воздействия 1(t); H(■) - колоколообразная функция; С5 - параметр размытости. На них накла- дываются условия сходимости, которым они должны удовлетворять [3]:

C s >  0, s = 1, 2, ...; lim C s = 0, lim sC s = да , s ^да           s ^да

J H ' ( u ) du = 0,                 (5)

Q ( u )

C s J H ‘ ( u ) udu = - 1,

Q ( u )

lim s    c —¹ H I — | = 5 ( т — t ), u = —,

I Cs )

limssCs = да, Cs > 0, s = 1, 2,..., Cs ^ 0.(6)

Переходная функция h ( t ) связана с весовой функцией k ( t ) соотношением [3]:

h (t) = dk^,(7)

dt

Тогда непараметрическая оценка весовой функции примет следующий вид:

( ks = hs (t) =----E ki- H 'I—i- s ■ C ,=       I c

.

Подставив оценку весовой функции в интеграл Дюамеля, получим непараметрическую модель ЛДС, после чего, заменив интеграл его дискретным аналогом (суммой), будем иметь непараметрическую расчетную модель линейного динамического элемента системы:

1    " t /”     1 1 — т j - t i 1

x s = k s ⁽⁰⁾ ■ u ⁽ t ) +— EE ^H 1 —-— I ^{u ( t} j ^{) Ат} , ⁽⁹⁾ s ■ ^Cs i = 1 j = 1 I      ^Cs      )

где т - переменная интегрирования, которая изменяется с дискретностью Ат .

А теперь рассмотрим задачу идентификации нелинейной системы для моделей Винера и Гаммерштей-на.

Модель Винера. Предположим, что структура нелинейного элемента в модели Винера (см. рис. 2) задана с точностью до набора параметров, т. е. выход исследуемого объекта вычисляется как некоторая функция от интеграла Дюамеля:

x ( t ) = f { w ( t ) , a } , (10) где x ( t ) - выходной сигнал системы; w ( t ) - выход линейной части системы (не измеряемый); u ( t ) - входной сигнал системы; f { } - нелинейный оператор.

Математическая модель нелинейного объекта может быть представлена в виде системы уравнений (9), (10), в которых вместо весовой функции h ( t ) и параметров a используются их статистические оценки. Эти оценки могут быть получены, если при тех же условиях эксперимента, в которых были получены реализации { u i , x i }, i = 1, s , сформировать выборку { u i ,®Д, i = 1, s .

Для некоторых классов нелинейных элементов выражение (10) может быть разрешено относительно ® ( t ) [4]:

_Ю ( t ) = f ^{- 1}( x ( t ), a ).                   (11)

В этом случае непараметрическая модель нелинейного объекта примет вид

x( t ) = f ( w ( t ), a ), w ( t ) = J h ( t - т ) u ( т ) d т .       (12)

Идентификация нелинейной системы с квадратором. Пусть имеется система, представленная в виде модели Винера, причем нелинейная часть этой системы представляет собой квадратор, описываемый функцией вида f ( p ) = cp ², где c - константа, а выход объекта вычисляется следующим образом: x ( t ) = f ( w , a ) = cw ².

При единичном входном воздействии u ( t ) = 1 выход нелинейной системы x ( t ) = cw ( t )², т. е. переходную характеристику линейного элемента w ( t ) = k ( t ) можно выразить через выход исследуемого процесса:

k ( t ) = 7 x ( t )/ c .                     (13)

При произвольном входном воздействии и нулевых начальных условиях выход линейной части системы описывается выражением (9). С учетом рассчитанного значения переходной функции (4) выход линейного элемента будет следующим:

1 -s_, t /А t I x_      к t — т j — t i ^

w ⁽ t ) = —EE J ~ H 1-------I ^{u ( т} j ^{) Ат .   (14)}

^scs i = 1 j = 1 V ^c (     ^cs     )

Тогда модель нелинейного объекта x ( t ) имеет вид

-т j - c

i st / А t    ( t xt ) = - EE V x i ; H j- s^c i = 1 i = 1

t )         I ²

- I u (_Ъ) Ат , (15)

где x 1 i - реакция нелинейной системы на единичное входное воздействие; u ( t ) - тестовое входное воздействие.

В качестве примера рассмотрим нелинейную динамическую систему, поведение которой имитируется следующим образом: линейная часть объекта описывается дифференциальным соотношением

2 ■ y "( t ) + 0,3 ■ у ‘ + 1,5 ■ y ( t ) = u ( t ), (16) а нелинейный элемент представляет собой квадратор вида (1) с параметром а = 4,37 (рис. 3).

Идентификация нелинейной системы с насыщением. Пусть нелинейное звено системы описывается функцией вида (2). В данном случае при w ( t ) < а выход объекта совпадает с выходом его линейной динамической части. В остальных случаях выход объекта представляет собой константу, которую можно определить опытным путем в результате нескольких статических экспериментов [1].

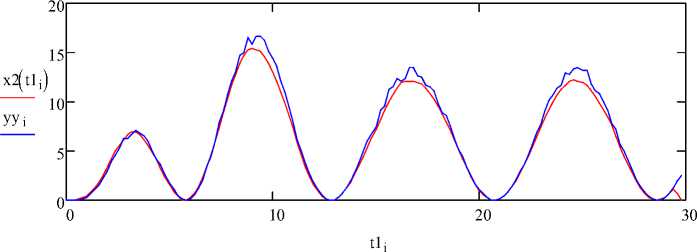
Рис. 3. Модель нелинейной системы x 2( t ) с выходом yy_i , объемом выборки s = 150, шагом дискретизации h = 0,2, помехой 5 %, входным воздействием u ( t ) = 2cos(0,4 t ) и относительной средней ошибкой моделирования 2,5 %

x2( tli)

yyi

t1 i

Рис. 4. Модель нелинейной системы x 2( t ) с выходом yy_i , объемом выборки s = 250, шагом дискретизации h = 0,12, помехой 5 % и относительной средней ошибкой моделирования 5,8 %

Для построения модели выполним следующие действия:

• 1)    проведем ряд статических экспериментов, т. е. последовательно подаем на вход системы некоторые константы, в результате чего можно сделать вывод о значениях параметров функции, описывающей нелинейную часть системы;

• 2)    получаем оценку нелинейного элемента системы, параметры которого определяются согласно следующему алгоритму:

• –    проведем серию экспериментов, в ходе которых будем подавать на вход системы воздействия u i j = C j , C j = const, в результате получим выборку { u , j , x , j }, i = 1, ⁵ , j = 1, m ;

• –    находим расстояние между двумя соседними измерениями: hh j = | x i j - x i - 1 j ^h ;

• -    если hh j < e , e >  0, b = x i j ;

• -    если x i j = b , то X j = y, - 1 j a = M { a j };

• 3)    подаем на вход объекта ступенчатую функцию, амплитуда которой не превышает значения порога b , получаем переходную характеристику и строим модель линейной части объекта в виде интеграла Дюамеля;

• 4)    строим модель объекта, выход которой вычисляется как значение функции, описывающей нелинейное звено с аргументом – выходом модели линейной части объекта.

Рассмотрим нелинейный динамический объект, линейная часть которого описывается дифференциальным соотношением

• 2,9 ■ y "( t ) + 1,27 ■ y ‘ ( t ) + 1 - y ( t ) = u ( t ) , (17) а нелинейный элемент представляет собой звено насыщения с параметрами b = 5, b 1 = 2, u ( t ) = 5sin( t ) (рис. 4).

Анализ работы модели нелинейного динамического объекта с видами нелинейности «звено насыщения» и «квадратор» позволяет сделать следующие выводы: полученная непараметрическая модель адекватно описывает систему при различных значениях параметров нелинейной части объекта, в условиях зашумленности каналов связи, при различном объеме выборки и различных входных воздействиях.

Модель Гаммерштейна. Рассмотрим систему, поведение которой может быть описано с помощью модели Гаммерштейна (см. рис. 2). Выход нелинейного элемента ro ( t ) в данном случае измерению недоступен. Предполагается, что параметризованная структура ЛЭ не известна, а нелинейная характеристика НЭ известна с точностью до набора параметров.

В модели Гаммерштейна связь между входом u ( t ) и выходом x ( t ) объекта при нулевых начальных условиях может быть описана уравнениями вида [4]:

t

w ( t ) = f ( u ( t )), x ( t ) = J h ( t -т ) ю ( т ) d t , (18)

или, исключая переменную ю ( t ),

t x (t) = J h (t-t) f (a, u (t)) d t,               (19)

где h ( t ) - весовая функция динамического элемента; f ( a , u ) - нелинейная функция, заданная с точностью до вектора неизвестных параметров a .

Пусть x 1( t ) - реакция нелинейного объекта на входной сигнал в виде функции Хевисайда u ( t ) = 1( t ), x ( t ) - реакция объекта на тестовый сигнал, форма которого отличается от ступенчатого. Измерения сигналов x 1( t ) и x ( t ) в дискретные моменты времени образуют выборки наблюдений {1, x 1 i } и { u i , x i } i , i = (1, s ), соответственно.

Ступенчатый сигнал u(t) = 1 после прохождения нелинейного элемента сохраняет ступенчатую форму, но меняет амплитуду, т. е. ю1(t) = f (a, 1(t)) = c1, где c 1 - константа. Тогда выход нелинейной системы t x1( t) = J h1( t - t)1(t) d t можно рассматривать как пе-0

реходную функцию линейной системы с весовой функцией h 1( t ). Оценка этой функции М( t ) может быть получена на основе выборки ( x 1 i , t i , i = 1, s ).

С учетом оценки h1(t ) модель нелинейной системы (19) можно записать в виде tt

x ( t ) = J h ¹ ( t - t ) w ( t ) d t = J h ¹ ( t - t ) f ( u ( t ), a ) d t . (20) 0                         0

Оценки параметров a находятся на основе выборки измерений { u i , x i }, i = 1, s ), реакции объекта x ( t ) на входной сигнал u ( t ) произвольной формы как решения экстремальной задачи.

Таким образом, нами в общем виде получены алгоритмы, позволяющие строить непараметрические модели нелинейных динамических систем, представленных в виде последовательного соединения линейного и нелинейного звеньев. Эти алгоритмы не предусматривают наличия полной априорной информации о структуре объекта.

Определение типа нелинейности моделей Винера и Гаммерштейна. Пусть исследуемая система может быть описана в виде модели Винера, вид нелинейности которой неизвестен.

Если подать на вход системы единичное воздействие, то выход ее линейной части w ( t ) = k ( t ) будет стремиться к неизвестной константе С 1, а выход нелинейного объекта - к величине, равной fC 1) . При некотором произвольном постоянном входном воздействии u ( t ) = C w ( t ) = Ck ( t ), q ( t ) = f ( Ck ( t )). Проведя серию экспериментов над данной системой, в ходе которых будем подавать на ее вход различные константы, получим выборку

{U , Q }: U = { u„u 2 ,..., u_c }, Q = { q„q 2 ,..., q_c },    (21)

где q_i - установившееся значение выхода системы при входном воздействии u i , причем значения q i будут пропорциональны fu i ), т. е. q i = C 2 f ( u i ), С2 = const.

На основании полученной выборки можно построить непараметрическую оценку функции нелинейного звена объекта q = f ¹ ( u ) = f ( u ):

ss f 1(u)=Zq1HI u^ I/ZHI u^ I (22) i =1 V C J/ i =1 k CS J где q1i - установившееся значение выхода системы при входном воздействии u 1 i; H(•) - колоколообразная функция; С5 - параметр размытости.

Далее получим оценку функции u = f 2( q ) = f 1 ( q ):

ss f 2( u) = Z u1iH Iq 1/Z н I / I (23) i =1 V C5 J/ i =1 V C5 J

При этом в общем случае восстанавливается лишь часть нелинейного звена fp ) при t > 0, однако нам необходимо восстановить вид функции при любом аргументе. Для этого предположим, что функция нелинейного звена симметрична относительно оси ординат f (- p ) = f ( p ) или f (- p ) = - f ( p ).

Таким образом, будем считать, что вид нелинейности системы известен. При этом значения переходной функции линейного звена объекта k ( t ) могут быть рассчитаны следующим образом:

k ( t ) = f ^{- 1}( q ( t )) = f 2( q ( t )) .

При произвольном входном воздействии модель линейного элемента следующая:

1 st IA t              t-т \ t * t w (t) = — ZZ f 2(q1i) ■ HI---— I u (t^^t, (24) scs , =1 j=1                 V     cs     J а выход нелинейного объекта - x(t) = f 1( w(t)).

Тогда непараметрическая модель примет вид

x ( t ) = f 1

1      5 11 A t

—ZZ f 2( x . ) ■ H'

sc. i =1 j =1

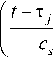
^- t i

u ( t j ) At

где x i - реакция нелинейной системы на единичное входное воздействие; u - тестовое входное воздействие.

Рассмотрим систему, в которой линейная часть объекта описывается дифференциальным соотношением

2 ■ У"(t) + 0,3 ■ у ‘(t) + y (t ) = u (t), а нелинейный элемент представляет собой звено насыщения с параметрами b 1 = 2, v0 = 0,4 (рис. 5).

Полученная непараметрическая модель адекватно описывает данную систему при различных видах нелинейной части объекта, в условиях зашумленности каналов связи, при различном объеме выборки и входных воздействиях.