О непараметрических алгоритмах моделирования и управления дискретно-непрерывным процессом

Рассмотрим задачу управления дискретно-непрерывным процессом, входные и выходные характеристики которого имеют вид вещественных, целочисленных и булевых переменных. Схема управления такого рода процессами представлена на рис. 1.

На первом этапе (ключ К 1 разомкнут) решается задача идентификации; на втором этапе ключ К 1 замкнут, решается задача управления объектом с участием ЛПР, после этого ключ К ₂ замыкается.

При управлении дискретно-непрерывными процессами целесообразно использовать теорию адаптивных и обучающихся систем, так как задачи идентификации, управления и принятия решения в стохастических системах рассматриваются в условиях непараметрической неопре деленности (когда неизвестна параметрическая структура модели исследуемого процесса), то предлагается использовать регрессионные модели.

Пусть х, u, ц _t являются наблюдаемыми переменными, где t - дискретное время. Необходимо найти алгоритм работы управляющего устройства для выработки управляющего воздействия на систему такого, что выход процесса в каждый текущий момент времени (t = 1,2 ...) как можно меньше отличался от желаемого x * ( t ) .

Для решения задачи управления используем элементы непараметрического подхода [1-3].

Непараметрический подход предполагает использование непараметрической оценки регрессии в качестве модели истинных зависимостей.

Условное математическое ожидание М^х\и, ц} является оптимальной, в смысле квадратичного критерия

R = M {( X - x )² \ u } = min            (1)

x моделью истинных зависимостей. Здесь x - оценка вектора выхода объектах

где s - размер обучающей выборки, с помощью которой методом скользящего экзамена выбирается оптимальный на этой выборке С_х

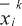
sl

= I V ПФ n=1      m =1

' u m - u nm Cx^k

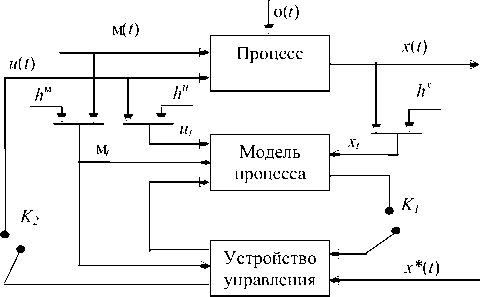
Рис. 1. Схема управления процессом:

x ( t ) = ( x 1 ( t ),..., x^k ( t ) ) - вектор выходных переменных процесса; u ( t ) = ( u '( t ), ..., U m ( t ) ) и Ц ( t ) ^ЦД t ), ..., Ц n ( t ) )

- соответственно управляемые и неуправляемые контролируемые переменные, состоящие из т и п компонент;

^(t) - случайные возмущения; hЦ, hu, hx - случайные ошибки измерения, такие что M{h} = 0, D{h} < ^;

x ( t ) - желаемое значение выходной переменной; t- время

sl / ЕП Ф n = 1 m = 1

' u m - u nm Cx^k

n * i .

\

'

J

Последовательный непараметрический алгоритм управления. Пусть мы имеем ситуацию, когда отсутствует обучающая выборка, а текущая информация об объекте поступает в устройство управления последовательно (активное накопление информации), тогда обучающийся непараметрический алгоритм управления на такте t ~s имеет вид:

u_s = й[ + Аи_х ,                  (9)

где и -оценка вектора входа, A us -изучающая добавка [3], й!е (и^j- ,u^j ),                  (10)

min , max ^,

б’ =

s - 1       k

I u/ПФ i=1     p=1

:* P - x p

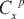
n

П Ф

^P = 1

'hP-Ц P cP H

l

П Ф

J j = 1

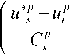
s - 1 k

1П Ф

: * P - xf

n

П Ф

^P = 1

'h P -h P c^{P ц}

l

П Ф

J j = 1

\

,

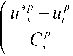
Используя необходимое условие минимума, т. е. приравняв производную функции R по искомой величине x к нулю, получим:

dR / dx = - 2 M {( X - x ) | u } = 0

и отсюда

x =M{X]u, ц}.             (2)

Непараметрическая оценка регрессии для векторно

го случая имеет вид:

k xs+1

s

l

= I x k П ф

i = 1

j = 1

sl

/ 1П ф

i = 1 j = 1

u s+ 1

-

_u J ₂

Cxk

/

u s+1 - ui Cx^k

где Ф(г) - колоколообразная функция, ядро которой и параметр Cs выбираются из условий [3].

Примеры треугольного, параболического и кубичес

кого ядер

^Ф( ^z )

1—\z\, ifW 1 , . 0,if\z\> 1 ,

^Ф( z ) =

(3/4)(1 - z ²), if\z\ <  1 , 0, if \ z \ >  1 ,

(4);

j = i, m , ^s pv-.m, /e⁽ u min , u max ) , ⁽¹²⁾ где u ³ определяется ЛПР на каждом такте принятия решения. Но ЛПР может определить не все значения компонент вектора и, поэтому l <  m .

На начальном этапе управления, когда фактически идет процесс обучения, доминирующую роль играет изучающая добавка. Связано это с малой «обученностью» системы и соответствует выработке пробных шагов, которые могут носить случайный характер, если отсутствует дополнительная априорная информация. По мере изучения объекта все большая роль, при формировании u s начинает принадлежать и'[.$].

При управлении реальным процессом естественно использовать опыт обслуживающего персонала (оператора, технолога-эксперта). Для того чтобы использовать опыт эксперта при решении этой задачи, формулу (11) в алгоритме (9) следует модифицировать в форме, рассматриваемой ранее.

Непараметрический алгоритмуправлениясобучаю-щей выборкой Пусть { u ( t ), ц ( t ), x ( t ), t = 1, s - 1} -обучающая выборка, состоящая из наблюдения входа и выхода объекта.

Непараметрический алгоритм управления в этом случае имеет вид:

^ф( z ) =

(1 + 2\ z \)(1 - \ z \)², if \ z \ < 1 , 0, if \ z \ > 5 .

U А

s - 1        k

I u / П *

i = 1      P = 1

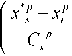
n

П Ф

^P = 1

'h P -h P с^P

Ц

l

П Ф д = 1

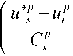
Параметр размытости C_x выбирается из условия выполнения минимума квадратичного критерия

s - 1 k

1П Ф

: * P - x P

n

П Ф

^P = 1

'h P -H P с^P

Ц

l

П Ф

J j = 1

\

,

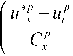
R = I ( X - X - ( C_x ))² ^ min , i = 1                                  Cx

j = 1, m , ^s-^{2, з,} ^ ^,и i'e ( u min , u max ) ^, l <  m .     ⁽¹³⁾

Алгоритм (13) представляет собой оценку обратной регрессии по наблюдениям { u ( t ), ц ( t ), x ( t ), t = 1, s - 1} .

В случае если компонентами вектора ц i , кроме вещественных переменных, являются переменные типа целочисленных и булевых, обучающиеся непараметрические алгоритмы несколько модифицируются.

Рассмотрим модификацию непараметрического обучающегося алгоритма управления с обучающей выборкой в данном случае:

V k ( x * f - x f ' n Гц, p -ц , )т f u ’ h - u h V fro ; -ro ' У

I u П ^ф 1 ,   ,П ®I^ P ^ П ^ф 1 a c^ П ^ф 1 йс^ П ⁿ ( w * ^- w * )

" fn ®f x f - x f ' п фГ^м 'll фГ u u In ф^ hq w - w*)

:■-I  I  C/    =■  t c-'  ГП  I C  Г■'  I  cro  J^='

j = 1,m, 5^2,3, ..., uie(uj- ,uj     l < m.(14)

min, max ,, где сиг- соответственно размеры векторов ro (t) и w(t), 1, если w* = w*, 0, иначе.

“ ( w - w * ) = (

Применение непараметрических моделей и алгоритмов управления в процессах сжигания угля в котлоагрегате энергоблока. Вспомогательное технологическое оборудование, установленное на энергоблоке Красноярской ГРЭС-2, предназначено для поддержания заданного режима работы энергоблока. Данное оборудование в большинстве случаев является исполнительным звеном в многоконтурной системе управления. Схема регулирования котлоагрегатом приведена на рис. 2.

Энергоблок охвачен шестнадцатью контурами управления. На каждом контуре управления энергоблоком установлен регулятор. Регуляторы выполнены на аппаратуре серий РПИБ-Ш, РПИБ-Т, РПИБ-М. Данные устройства являются регуляторами по отклонению и используют стандартные ПИ, ПИД законы регулирования.

Ниже приводится описание основных регуляторов котла.

Регулятор температуры острого пара предназначен для поддержания заданной температуры острого пара за котлом путем изменения количества впрыскиваемой воды паровой тракт котла.

Регулятор расхода питательной воды является регулятором уровня в барабане котла.

Регулятор первичного воздуха предназначен для поддержания заданного значения мощности электродвигателя шахтной мельницы (ШМ) с заданной неравномерностью путем изменения подачи первичного воздуха.

Регулятор тепловой нагрузки (РТН) предназначен для стабилизации заданного тепловыделения в топке котла путем воздействия на станцию бесступенчатого регулирования оборотов питателя сырого угля ПСУ (СБР.ПСУ) и через динамическую связь на регуляторы первичного воздуха.

Главный регулятор блока № 5 предназначен для поддержания заданного давления перед турбиной, определяющего соответствие между нагрузкой турбины и суммарной нагрузке котлов (А и Б).

Регулятор уровня конденсата в конденсаторе - за конденсатными насосами установлен 3-ходовой комбинированный клапан рециркуляции, который осуществляет распределение подачи конденсата в деаэратор (6 атмосфер) или обратно в конденсатор, в зависимости от уровня в конденсаторе.

Регулятор давления в деаэраторе 6 ата предназначен для поддержания нормального процесса деаэрации, путем регулирования постоянного давления в головке деаэратора.

Регуляторы уровня в подогревателях высокого давления ПВД и подогревателях низкого давления ПНД предназначены для поддержания заданного уровня дренажа греющего пара в подогревателях, этим обеспечивается более экономичная работа регенеративных подогревателей.

Стерегущий регулятор давления пара перед турбиной - этот регулятор работает в «стерегущем» режиме и вступает в работу при снижении пара пред турбиной до 95 кг/см3 или 83 кг/см3 на блоке № 5. Регулятор давления

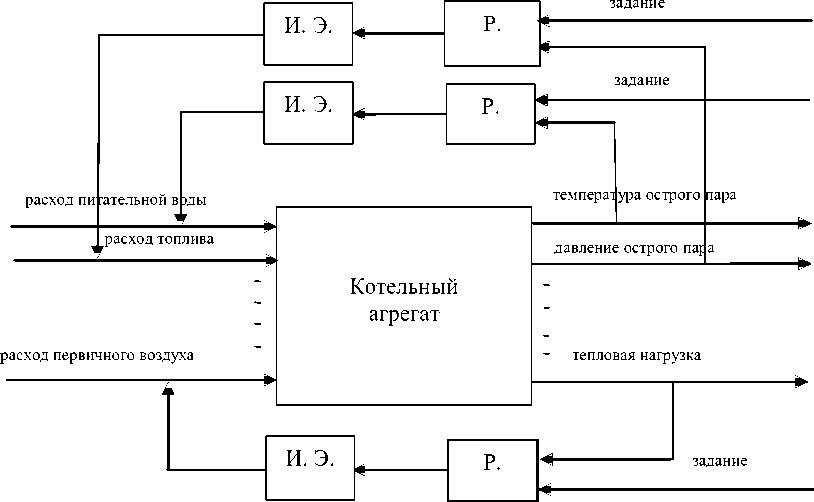
Рис. 2. Краткая схема системы регулирования энергоблоком

вторичного пара пароперегревательного устройства (ППУ) предназначен для поддержания заданного значения давления вторичного пара.

Ниже представлены результаты обработки данных, снятых с блока котлоагрегата (рис. 3,4).

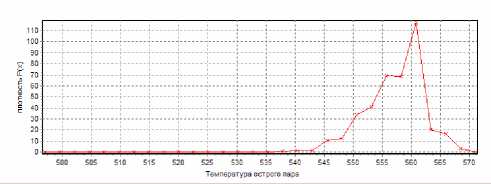
Рис. 3. Результаты обработки данных блока котлоагрегата

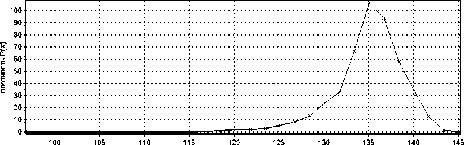
Давление острого пара

Рис. 4. Результаты обработки данных блока котлоагрегата

Данные представлены в виде плотностей распределения вероятности.

Предложенные обучающиеся непараметрические алгоритмы управления могут быть модифицированы и использованы при разработке реальных компьютерных систем управления дискретно-непрерывными процессами, часто встречающихся на предприятиях стройиндустрии, химии, теплоэнергетики и др. Приведены графики оценок плотностей распределения температуры острого пара для энергоблока Красноярской ГРЭС-2.