О непараметрических алгоритмах управления дискретно-непрерывными процессами

Предложены схема и алгоритмы управления дискретно-непрерывными процессами. Рассмотрены модификации алгоритмов, учитывающие взаимодействие с лицом, принимающим решение, наличие вещественных, целочисленных и булевых переменных.

Рассмотрим задачу управления дискретно-непрерывным процессом, входные и выходные характеристики которого имеют вид вещественных, целочисленных и булевых переменных (см. рисунок).

Схема управления процессом

Регрессия (условное математическое ожидание) является оптимальной, в смысле квадратичного критерия

R = M {( X - x )² | u } = min ,            (1)

x моделью истинных зависимостей. Здесь x - оценка вектора выхода объектаА.

Используя необходимое условие минимума, т. е., приравняв производную функции R по искомой величине x к нулю, получим dR / dx = - 2 M {( X - x ) | u } = 0, отсюда

5с — М {^ и }.                  (2)

Непараметрическая оценка регрессии для векторно

го случая имеет вид

k xs +1

s

l

- Z x k п *

i = 1

J = 1

/

u s + 1 j

-

u i ^j

\

V

Cx ^k

sl

/ дп

i = 1 j = 1

' u s j u i¹

Cx

V

)

где Ф

u s + 1 j ^{- u}i’

k

Cx

ядро функции, выбирается из следую-

На рисунке приняты следующие обозначения: х ( t ) = ( x 1 ( t ),..., x k ( t ) ) - вектор выходных переменных процесса; u ( t) = ( u 1 ( t ),..., u m ( t ) ) и ц ( t ) = ( ц 1 ( t ), ..., ц n ( t ) ) - соответственно управляемые и неуправляемые контролируемые переменные, состоящие из т и п компонентов; ^ ( t ) - случайные возмущения; h ^p , h^u , h x - случайные ошибки измерения, такие что M { h } = 0, D { h } < ~ ; x ( t ) - желаемое значение выходной переменной, t- время.

На первом этапе (ключ К , разомкнут) решается задача идентификации; на втором этапе (ключ К 1 замкнут) решается задача управления объектом с участием лица, принимающего решение (ЛПР), после этого ключ К ₂ замыкается.

При управлении дискретно-непрерывными процессами целесообразно использовать теорию адаптивных и обучающихся систем. Задачи идентификации, управления и принятия решения в стохастических системах рассматриваются в условиях непараметрической неопределенности (когда не известна параметрическая структура модели исследуемого процесса), поэтому предлагается использовать регрессионные модели.

Пусть х , и , p t , где t - дискретное время, являются наблюдаемыми переменными. Необходимо найти алгоритм работы управляющего устройства для выработки такого управляющего воздействия на систему, что выход процесса в каждый текущий момент времени ( t - 1,2, ...) как можно меньше отличался бы от желаемого x * ( t ) .

Для решения задачи управления используем элементы непараметрического подхода [1...3], который предполагает использование непараметрической оценки регрессии в качестве модели истинных зависимостей.

щих условий:

W

- | ф ( z ) dz = 1,

где г

u s + 1 ^{j -} u? Cx^k

-<х>

-ядро функции колоколообразное, т. е. Ф(z 1) < Ф(z2), для | z21< Z11;

- j z p Ф ( z ) dz <~ , ^- 2,3, ....

Параметр размытости Cx ядра Ф удовлетворяет усло виям Cx ^ 0 и nCx (n) ^ “ . n ^~          n ^^

При выполнении двух условий оценка x является асимптотически несмещенной, состоятельной, асимптотически нормально распределенной.

Приведем примеры треугольного, параболического и кубического ядер:

Ф ( z ) =

[ 1 - I z I, if I z l < 1, [ 0,if| z | > 1;

Ф ( z ) = fO/^X! ^- z ²),i^f| z | < 1, [         0, if I z | > 1;

_Ф( z ) =[ (1 + 2 | z |)(1 - | z |) ² , if | z | < 1, 0, if | z |> 5.

Параметр размытости C _x выбирается по условию выполнения минимума квадратичного критерия:

s

R = £ ( Xi - X -( Cx ))² ^ min,         ⁽⁷⁾

Cx i=1

где ^ - размер обучающей выборки, с помощью которой методом скользящего экзамена выбирается оптимальный на этой выборке C :

X

Вестник Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева

s

l

X ik = 2 x nk П

n = 1

m = 1

m u _i

^^^^^^

m u n

V

k Cx _j

sl

/ 2Пф n=1 m=1

m u _i

^^^^^в

m u n

V

k Cx _j

n Ф i ■ (8)

Рассмотрим последовательный непараметрический

Пусть { u ( t ), p ( t ), x ( t ), t = 1, s - 1} - обучающая выборка, состоящая из наблюдения входа и выхода объекта^ Непараметрический алгоритм управления в этом случае

алгоритм управления .

Пусть мы имеем ситуацию, когда отсутствует обучающая выборка, а текущая информация об объекте поступает в устройство управления последовательно (активное накопление информации) Тогда обучающийся непараметрический алгоритм управления на такте t = s имеет вид йs = иsj + Aus ,                  (9)

где u -оценкавектора входа; A u^J_s -изучающая добавка [3],

имеет вид

j us =

s - 1      k

Z u / П ф i = 1 f= 1

s - 1 k

2П

I = 1 р = 1

~

u

j

s

* f

x s

- x f

С f

C _x ^l____

Пф

P s^f  !' ^р

р = 1

Г f

^{1 С ц}

* р

x s

Г f

C _x

s -1

k

P s^f  !' ^f

p сц

Y i_

Пф

=

э ^f и^р u ^{s -} u i

C x

,(13)

^u 1 ^{e (} u mjn , u _max) ^,

2 u i П ^ф

( * f

/

i =1

f =1

k

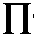
f =1

l

A

n xi xs

A,

. * f xs

C x^f

C

^{- x}i

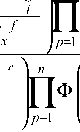
A

p

C ц

P ^f

j = 1, m , s = 2, 3,... ■

P ^f

P ^f

p

C ц

P ^f

A

A

,

j = l m , ^{s _ 2, з,} ^ ^, у e⁽ u min , u max ) ^, ' <  m ■

Алгоритм (13) представляет собой оценку обратной регрессии по наблюдениям { u ( t ), ц ( t ), x ( t ), t = 1, s - 1} ■

В случае если компонентами вектора u i , кроме веще

ственных переменных, являются переменные типа целочисленных и булевых, обучающиеся непараметрические алгоритмы несколько модифицируются^

Рассмотрим модификацию непараметрического обучающегося алгоритма управления с обучающей выборкой в этом случае:

На начальном этапе управления, когда фактически идет процесс обучения, доминирующую роль играет изучающая добавка^ Это связано с малой обученностью системы и соответствует выработке пробных шагов, которые могут носить случайный характер, если отсутствует дополнительная априорная информация^ По мере изучения объекта при формировании u s все большая роль начинает принадлежать и ^j [ s ] ■

'

u

s =

s - 1       k

Z u j П ф i = 1 f = 1

s - 1 k

2П ф i = 1 f = 1

[ * ^f f A n f f i Г э h h A c r r ) v x s -^       П ф| u i?" П ф| C^- П*

C x     j f = 1    i   C -ц    7 h = 1    i    C x     jr= 1    i   C ”    j q= 1

' *f fA n ( f р^i I эh hA c ( r r\v , xs^xL I ф|еГгнТ   ^luszuc I ф|“sZ^L 1 h(wq i -xf  1^11 -цf tIL1 i  -h  п i -”  jq/s

q w i

j = ¹, m , ^s- ^2,3, ^ ^, ui ^{j e ( u} m in , u ,)ax ) ^, i <  m ^,

где с и г - соответственно размеры векторов ю ( t ) и w ( t );

fi ( w sq

- w q ) =

1,

0,

если w j = w f , иначе.

При управлении реальным процессом естественно использовать опыт обслуживающего персонала (оператора, технолога-эксперта) Для того чтобы использовать опыт эксперта при решении этой задачи, формулу (11) в алгоритме (9) следует модифицировать в виде

Таким образом, предложенные обучающиеся непараметрические алгоритмы управления могут быть модифицированы и использованы при разработке реаль

ных компьютерных систем управления дискретно-непре

рывными процессами

~

u

s - 1      k

Z u / П ф

' j = i = 1     f = 1

s

s - 1 k

2П i=1 f=1

( * f x s

^^^^^s

x f ^A

n

и ^f

^^^^^s

и ^f

с ^f C _x

V7

„ * ^{f fP x} s ^- x i

f = ¹

n

V иf

p

^- ц

Пф

u "^f - u f

^^^^^s

И ^f

j = 1

-/ x

V

f = ¹

C ^f l ^{- ц}

Пф

V

Г э f и s

C x

3 - u f

,(12)

j = 1

C x V7

j = ¹ m , ^s- ²,³, ..., у e⁽ u min , u max ) , где u ^э определяется ЛПР на каждом такте принятия ре-шения^ Но ЛПР может определить не все значения ком-

понент вектора и , поэтому ' <  m ■

Далее рассмотрим непараметрический алгоритм управления с обучающей выборкой