О непараметрических оценках функции регрессии и ее производных при наличии пропусков данных

Проблема моделирования дискретно-непрерывных процессов является одной из центральных в кибернетике. Определяющее значение при постановке задачи идентификации имеет математическая постановка, соответствующая различным априорным предпосылкам. Априорные сведения о процессе, по существу, определяют подход к задаче идентификации.

Ниже мы остановимся на задаче идентификации и связанной с ней задаче оценивания соответствующих вероятностных характеристик в условиях непараметрической неопределенности. В отличие от ставшего традиционным параметрического подхода к решению задачи идентификации в дальнейшем нам понадобятся некоторые качественные свойства поведения исследуемого процесса. Одним из главных этапов на пути решения этой задачи является оценивание регрессионных характеристик входных-выходных переменных процесса.

Непараметрический уровень априорной информации не предполагает наличия этапа выбора параметрической структуры модели, но требует некоторых сведений качественного характера о процессе, например от однозначности или неоднозначности его ха- рактеристик, линейности для динамических процессов или характере нелинейности. При идентификации линейных динамических объектов мы сталкиваемся с необходимостью оценивания производной функции регрессии. Это связано с оценкой весовой функции линейной системы по измерениям функции переходной характеристики последней. Непараметрическая модель в этом случае представляет собой оценку интеграла Дюамеля.

Существенная особенность данного исследования состоит в предположении, что исходные выборки содержат пропуски данных при контроле входных-выходных переменных объекта. Это приводит к необходимости построения модифицированных непараметрических оценок функции регрессии и ее производных.

Пусть имеется неравномерная выборка статистически независимых наблюдений (ui,xi), i = 1,s, входных и выходных переменных системы объемом s. Здесь ui – значение вектора наблюдений входных воздействий размерности m в i-й точке выборки, а xi – значение выходного воздействия в этой точке. Требу- ется построить непараметрическую модель объекта и восстановить производную первого порядка стохастической зависимости x(u) по имеющейся выборке наблюдений.

На начальном этапе восстановления

x ( u ) V x e Q ( x ) принимается статистика [1]:

sm

x( u) = £ Xj ПФ

j =1      k =1

где Ф ( z ) - колоколообразная функция, удовлетворяющая следующим условиям [1]:

Ф ( z ) <м , V z eQ ( z ), J Ф ( z ) dz = 1,

D( z )

1       I u^J - t^j I

Ф² ( z ) dz <«, lim-- ф| -------l = 5 ( u^j - t^j ), s ^ra

Q( z )                                s V s 7

здесь 5 ( u^J - t^j ) - дельта-функция Дирака, z - аргументы колоколообразной функции.

Параметр размытости С s должен удовлетворять условиям [1]:

Cs > 0, limCs = 0, lims ■ Csm = ra.(3)

s ^ra

На следующем этапе строится H -аппроксимация [2]:

k m           j*

Xk (u) =    Z X* П H   -(4)

kc k i =1 j =1 V c k 7

где { ( u * , x * ) } - рабочая равномерная выборка объемом k <  s ; c m ^ 0; kc k ^«; V J = 1,..., m. Тогда

• 1    Iu^j - t^J I _J ,

—H Il ^§ ( u^j - t^j ) с ростом k , где H ( z ) - ко- c k V ^c k 7

локолообразная функция, отличающаяся от Ф(z) на множитель, равный константе km

— Ф kcmZ У j*j u - ui   ।

i

ck

V u e Q ( u ).

Можно показать, что km      j *j

—Zn H I----~ l= 1 V u eQ ( u ).    (5)

kc k i =1 J =1     V ^c k 7

К классу функций H ( z ) и Ф ( z ) относятся, например, гауссова кривая и функция Соболева.

В качестве оценки производной регрессии предлагается взять аппроксимацию, построенную на рабочей равномерной выборке, в виде [3]:

k m              j      ^* j

D ^а x k ( u ) = T^ m Z x * П H^V) I u-^u^ l ,     (6)

^kc k i =1     J =1        V ^c k 7

где a = ( a ₁ ,..., a _m ), a _J = {0,1}, J = 1, m , если a _J = 1, то по переменной u ^j берется производная первого порядка, если a _J = 0, то производная нулевого порядка; H ^(/) ( z ) – функция, удовлетворяющая интегральным условиям, сформулированным ниже.

Если u - скалярная величина, т. е. m = 1, то оценка первой производной регрессии (6) при a = 1 является асимптотически несмещенной и состоятельной при выполнении следующих условий:

J H ^(,)( z ) dz = 0, c_k J zH ^(,)( z ) dz = - 1, R ¹                              R ¹

J H ^(//)( z ) dz .                    (7)

R ¹

Техника доказательства основывается на результатах [3].

Заметим, что обозначенные выше условия сужают класс функций, которые могли бы применяться в случае восстановления кривой регрессии. В частности, - z 2 e ²

гауссова кривая H ( z ) =       (рис. 1, а ) имеет произ-

2п водную H'(z) (рис. 1, б), которая сложна с вычислительной точки зрения, однако ее можно заменить кусочно-постоянным аналогом H> (z) (рис. 1, в). Отметим, что время вычисления H> (z) в 1,3 раза меньше, чем H'(z).

Рис. 1

Для выбора оптимального параметра размытости введем меру отклонения оценки (6) от истинной производной:

W ( c k ) = J ( Dx ( u ) - D ^a x k ( u ))² du ,       (8)

G ( u )

где G ( u ) – область сравнения. Тогда критерий оптимальности будет иметь вид

W ⁽ c k ) ^ min,                ⁽⁹⁾

n< c k )

где Q ( c k ) = (0, +« ). Но при практическом применении данный критерий невозможно использовать, так как D ^а x ( u ) неизвестна.

Преобразуем (9), используя формулу интегрирования по частям и тем самым понижая порядок производной. Тогда критерий оптимальности приобретет следующий вид:

I ( C k ) = J ( D ^a X k ( u ))² du -

G ( u )

• - 2 J xk (u)DaXk (u)|G() du_ +

G (u -)

+ 2 [ xk (u) D a xk (u) du ^ min, c G(u)

где u- = (u1,...,uj-1,uj+1,...,um), здесь j такое, что ау* 0, a+= (a,,..., aj_v ay +1, aj+„..., a m); xk (u) -оценка любого типа, которая в смысле некоторого критерия достаточно хорошо аппроксимирует нужную нам величину; G(u) c Q(u) - область хорошего качества оценки xk (u). Если это непараметрическая оценка, то вычисление оптимального параметра размытости становится рекуррентным. На первом шаге находится оптимальный параметр размытости ck0 для оценки кривой регрессии. На следующем шаге определяется оптимальный параметр размытости ck1 для оценки производной кривой регрессии первого порядка по какой-либо переменной. Критерий оптимальности на этом шаге имеет вид (10) при x(u) = x(u,ck) и a = (0,..., 0,1,0, ...,0).

При построении модели реального процесса иногда используются выборки случайной величины, результаты измерений которой распределены неравномерно. Это приводит к тому, что в некоторых подобластях пространства наблюдений образуются пустоты. В таких условиях приходится отказываться от применения стандартной непараметрической оценки регрессии.

При наличии пустот в пространстве наблюдения Q ( u ) непараметрическая оценка регрессии основывается на использовании не конкретного значения выходной переменной в j -й точке выборки, а ее оценки. Проводить это оценивание будем по представленному ниже алгоритму.

Пусть мы находимся в j -й точке выборки. Определим множество Л s соседних точек выборки, в которых колоколообразная функция не равна нулю:

m

u: Пф k=1

Л

Г u k - u k ^ ( C s^{i (}c s , Р s ) )

> 0 ^ ,

i = 1, s, j = 1, s, где ps - параметр оптимизации, а колоколообразная функция для каждой входной переменной uk , k = 1, m, расширяется в направлении разрежений в выборке, т. е. ее ветви имеют разные константы Липшица. Приведем пример такой асимметричной функции:

cos

1 u^k

l

•

—

uk

cos

uk

-

ф

uk

-

uki

C s

= <

0, if

cos

cos

0, if

C s

uk

C s

uk

-

uk

C s

k 1 u

-

•

l

k u

-

⁺ 2,

if -1 •

+ 1, if 0 <

> п I V

k u^k

uk

п <

-

uk

uk

—

uk

uk

-

C s

< 0

C s

uk

C s

< п

< -1 •п

C s

k u^k

C s

uk

-

uk

C s

,if J_s ( u^k + h , C s ) >  J_s ( u^k

-

h , c_s ),

+ 2, if

+ 2, if

> 1 •п Iv

-

0<

п<

uk

-

k u

k u

uk

C s

-

k u^k

C s

-

k u^k

< 1 •п

C s

< 0

,if f_s ( u^k + h , C s ) <  J_s ( u^k

-

h , c_s ),

<п

где h >  0 - радиус окрестности текущей точки и ; l >  1 - коэффициент расширения колоколообразной функции, при l = 1 колоколообразная функция принимает симметричный вид. Функция множества в виде непараметрической оценки плотности [4] с малым параметром размытости

S kk

• f, ( u k , C s ) = — £ф( u— u ^), k = 1, m , (12) SC s i =1 C s

применяется для определения сгущений и разрежений точек в выборке по каждой входной переменной u^k , k = 1, m . Форма и вид колоколообразной функции зависят от плотности точек выборки в h -окрестности текущей точки.

Рассмотрим выборку наблюдений входной переменной u i , i = 1,20 (рис. 2) с функцией множества (12) (рис. 3). Тогда график колоколообразной функции в точке u i = 0,26 при разных значениях коэффициента расширения l будет иметь вид, представленный на рис. 4 колоколообразная функция расширилась по направлению уменьшения значения функции множества в окрестности текущей точки u i = 0,26.

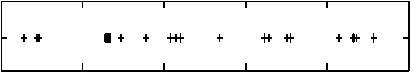
О              0.2             0.4             06             0.8 Я;

Рис. 2

+++ – точки, в которых производились измерения входной переменной объекта; – ui = 0,26

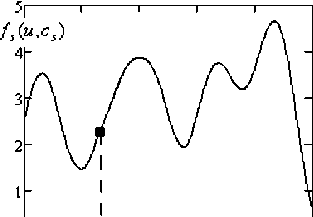
о1--------еЧ----------1-------1-------

(У,-/3) “- (Uj+A) 0 6     0®    “

---функция множества/(и)

Рис. 3

На подобласти Q ( x , u ), определяемой Л s , сформированной в соответствии с правилом (11), строится поверхность ф j ( u ) = р j V ( u ), j = 1, s , где T ( u ) - вектор базисных функций; p j - вектор параметров, определяемых по методу наименьших квадратов.

Для примера рассмотрим выборку наблюдений со скалярным входным и выходным воздействиями (ui, xi), i = 1,15 (рис. 5), где функции фj (u), j = 1,15, имеют линейный вид. На рис. 5 отмечена текущая де- сятая точка выборки и точки вокруг нее, колоколообразная функция Ф((u -ui)/Cs) в которых не равна 0. В данном случае их 4. Таким образом, вектор коэффициентов pj при наборе базисных функций Т(u) = (1, u)j определяется по методу наименьших квадратов на основании пяти выделенных точек.

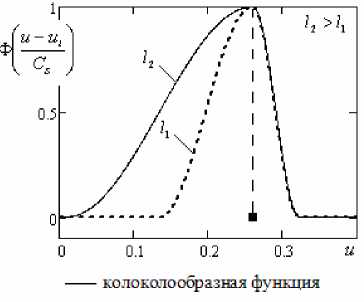
Рис. 4

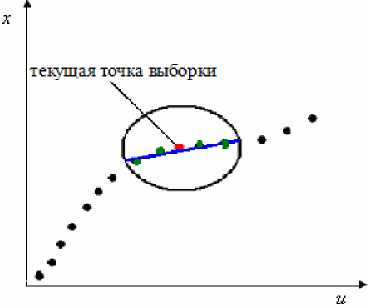
Рис. 5

Произведем модификацию непараметрической оценки регрессии следующим образом [5]:

x ( u , C s , р s ) =

Sm

X Ф j ( u П j =1 (          k =1

kk u - u j I CsJ(Cs , Ps ) J,

Sm

X№ j =1 k =1

kk

I u - u j [ C s^J ( C s , P s )

Параметр размытости в формуле (13) оценивается для каждой j -й точки из выборки наблюдений [6]:

• ^C s ^{j ( C} s , P s ) =P s ■ f s ^' u j , ^C s ), ^j = 1, ^s .        ⁽¹⁴⁾

Выбор оптимального параметра размытости c_s и коэффициента пропорциональности P _s осуществляется путем минимизации среднеквадратичного критерия:

1 ^s

W ^{( C} s , P s ) = X ⁽ x i ^{- :X(U} i ^{, C} s , P s )) ^ min- ⁽¹⁵⁾ s ~7                             ^Cs - ^{p s}

Другим методом непараметрического оценивания регрессии между входными и выходными воздействиями объекта является предварительное заполнение пустот в пространстве наблюдений случайной величины. Для этого используется следующая бутстреп-процедура [7].

• 1.    Точка u_l равномерной сетки, натянутой на область наблюдения Q _s ( и ) входных переменных u^k , к = 1, m , будет считаться пропуском, если

• 2.    По присутствующим наблюдениям ( u , x i ), i = 1, s входных и выходных переменных системы строится регрессионная модель (1), однако параметр размытости оценивается по формуле (14) для каждой точки выборки наблюдений, что позволяет избежать неадекватного поведения оценки (1) в областях разрежений (пустот) пространства наблюдений Q s ( и ).

• 3.    По построенной регрессионной модели находятся оценки x_si = x ( u i ), i = 1, s .

• 4.    Определяются ошибки б i = x i - x i , i = 1, s , для всех точек выборки.

• 5.    Для каждого пропуска после подстановки значения сопутствующей входной переменной u_l в полученное регрессионное уравнение находится оценка x ( u l ), l = 1, K .

• 6.    Значения выходной переменной, которыми замещают пропуски, получается по формуле

• 7.    Данные, полученные после заполнения пропусков, ( u l , x_sl ), l = 1, K , объединяются с исходной выборкой наблюдений ( u i , x i ), i = 1, s . По итоговой выборке объема s + K строится регрессионная модель (1).

m

П ^fs ⁽ u l, c s ) <  a , a >  0. ⁽¹⁶⁾ j =1

Пусть таких точек будет K , т. е. l = 1, K . Параметр a >  0 настраивается исходя из оптимизационной процедуры по среднеквадратичному критерию.

x si = x ( U i ) + б I , l = 1, K , (17)

где б l выбирается случайно из ошибок, рассчитанных в п. 4. Это можно реализовать следующим образом: с помощью генератора случайных чисел выбирается целое число q на интервале [1; s ], б l = б q , и операция повторяется для каждого б l , l = 1, K .

Приведем численные результаты моделирования при использовании модифицированной непараметрической оценки регрессии (13) в сравнении со стандартной непараметрической оценкой (1).

Пусть размерность входной переменной равна двум и имеется неравномерная выборка наблюдений ( u i , x i ), i = 1, s , объемом s = 200, u = ( u ¹, u ²), на области Q _s ( u ): { u ¹ e [0;0,5], u ² e [0;0,5] } ; x = ф ( u ) + £ , где

ф ( u ) = ф ( u ¹, u ²) = sin(7 ■ u ¹ + u ²); C - аддитивная центрированная помеха, имеющая нормальный закон распределения с математическим ожиданием M ( C ) = 0 и ограниченной дисперсией.

Помеха накладывается следующим образом:

• -    измеряется интервал изменения сигнальной части [ a ₁ ; a ₂ ];

• -    задается уровень помех h на интервале [0; 1];

• -    с помощью генератора случайных чисел формируется вектор С значений случайной величины, распределенной по нормальному закону с M ( С ) = 0, h ( a ₂ - a ,)

а(С) =---2---—. Вектор с складывается с вектором значений сигнальной части.

Создадим пробел в выборке наблюдений, расположение точек u i , i = 1,200, для которой приведено на рис. 6. С помощью генератора случайных чисел формируем вектор u ², | u ²| = 200, значений случайной величины, распределенной по равномерному закону на интервале [0; 0,5]. Затем генерируем векторы u \ и u 2 , l u ^ = | u 21 = 100, на интервалах [0;0,2] и [0,3;0,5] соответственно. Выборка наблюдений входных воздействий объемом 200 имеет вид ( u¹ и u 2 ; u ²).

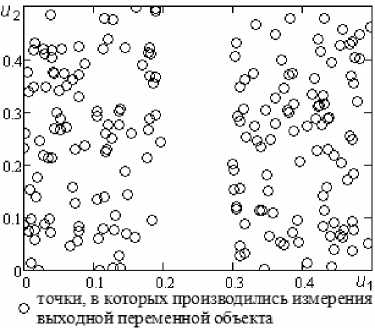
Рис. 6

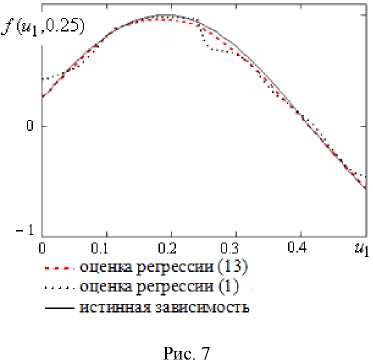
Пусть в каналах измерения выходного сигнала присутствует 5%-я помеха, т. е. h = 0,05, а ф j ( u ) = Р ₂ j u ² +Р ₁ j u ¹ +Р ₀ j , j = 1, s , имеет линейный вид, где u ² , u ¹ – входные переменные. Результат моделирования в виде среза ( u ² = 0,25, u ¹ = [0;0,5]) представлен ниже (рис. 7).

Среднеквадратичная оценка ошибки моделирования при использовании стандартной непараметрической оценки регрессии (1) равна 3,3 %. При использовании модифицированной оценки регрессии (13) с несимметричной колоколообразной функции оценка ошибки равна 1,5 %, что в 2 раза меньше, чем при ис- пользовании стандартной оценки. Оценка ошибки моделирования здесь и в дальнейшем рассчитывалась следующим образом:

J z ( ф ( ui) - x ( и))

E =   ------------100 %, где ui, i = 1,100 - вектор значений случайной величины, распределенной по равномерному закону на области Q5 (и).

Пусть размерность входной переменной равна четырем и имеется неравномерная выборка наблюдений ( u i , x i ), i = 1, 5 , объемом 5 = 400, и = ( и 1 , и 2 , и 3 , и ⁴), на области Q ₅ ( и ): { и ¹ е [0;0,5], и ² е [0;0,5], и ³ е [0;0,5], и ⁴ е [0; 0,5] } . И пусть в этой области имеются искусственно созданные пустоты по двум входным переменным: и ³ е [0;0,2] и [0,25; 0,5], и ⁴ е [0; 0,3] и [0,4; 0,5], i = 1,400 ; x = ф ( и ) + £ , где ^ - аддитивная помеха, имеющая нормальный закон распределения с M ( £ ) = 0 и D ( £ ) < « , а истинная зависимость имеет вид

ф ( и ) = ф ( и 1 , и ², и ³, и ⁴) = sin(0,45 ■ и ’ ) -- sin(0,5 ■ и ²) + sin(0,45 ■ и ³) - sin(0,5 ■ и ⁴).

Пусть в каналах измерения выходного сигнала присутствует 5%-я помеха. Тогда результат моделирования при помощи модифицированной оценки регрессии (13) в виде среза ( и ¹ = и ² = 0,2, и ³ = 0,4, и ⁴ = [0; 0,5]) будет представлен в виде линейного аппроксимирующего полиноми (рис. 8) и квадратичного аппроксимирующего полинома (рис. 9).

Оценка ошибки моделирования при использовании модифицированной оценки регрессии (13) с квадратичным аппроксимирующим полиномом ф j ( и ), j = 1, 5 , в 8,2 раза меньше, чем с линейным полиномом, и в 15,6 раз меньше, чем при использовании стандартной непараметрической оценки (1).

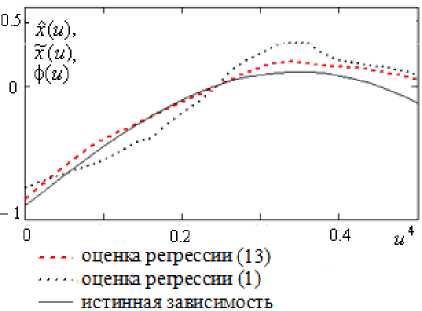
Рис. 8

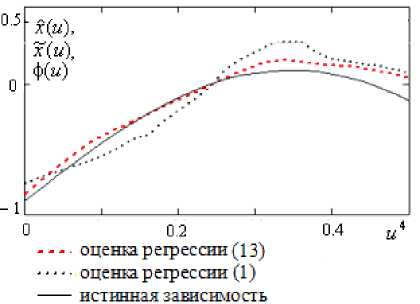
Рис. 9

Таким образом, результаты экспериментов, представленные на рис. 6–9, подтверждают, что использование модифицированной непараметрической оценки регрессии (13) с квадратичной аппроксимирующей функцией дает в несколько раз меньшую ошибку идентификации при наличии пустот в пространстве наблюдений, чем применение стандартной непараметрической оценки (1).

Выберем объект с одномерным входным и выходным воздействиями. Для этого примем ф ( и ) = 5( и - 0,5) 2 . Пусть объем выборки равен 5 = 30:

( и₁ , x i ), i = 1,30, а сама выборка наблюдений отно- си-тельно равномерна и не имеет больших пробелов.

Результаты моделирования, приведенные на рис. 10, показывают, что среднеквадратичная оценка ошибки моделирования при использовании стандартной непараметрической оценки регрессии (1) в 1,5 раза больше, чем при применении оценки регрессии (13) с несимметричной колоколообразной функцией и линейным аппроксимирующим полиномом.

Таким образом, при разреженной выборке, без явных пробелов в пространстве наблюдений, ошибка моделирования с использованием модифицированной оценки регрессии (13) меньше, чем с применением стандартной оценки.

Проведем сравнение результатов численного моделирования, полученных с помощью модифициро- ванной оценки регрессии (13) и бутстреп-метода со стандартной непараметрической оценкой (1).

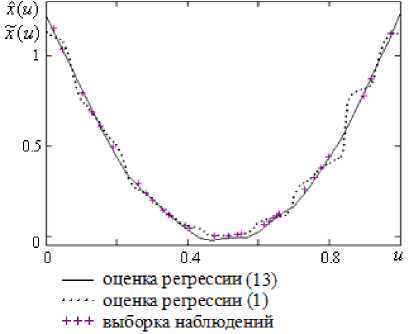
Рис. 10

Пусть имеется неравномерная выборка наблюдений одномерных входного и выходного воздействий объекта ( и, , x ), i = 1, s , объемом s = 20, и е [0;1], x = ф ( и ) + £ , где ф ( и ) = sin(5 ■ и ); ^ - 5 %-я помеха в каналах измерения выходного сигнала. Пусть ф j ( и ) = Р _{2 j}и ² + Р 1 j u + Р ₀ j , j = 1, s . Тогда результаты моделирования будут следующими (рис. 11, 12).

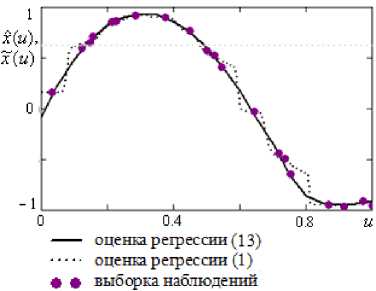
Рис. 11

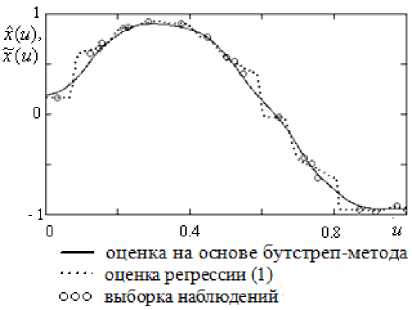
Рис. 12

Исходная выборка наблюдений входных воздействий может быть дополнена значениями наблюдений по бутстреп-методу (рис. 13).

0 titiix ** * #vW*Wt 4**^^ +**ЩДД*ЩЛ «

0        0.2       0.4       0.6       0.8 и,

♦♦* исходная выборка наблюдений ДДД «дополненные» наблюдения

Рис. 13

Среднеквадратичная оценка ошибки моделирования при использовании стандартной непараметрической оценки регрессии (1) равна 3 %, при применении модифицированной оценки регрессии (13)–1,45 %, а при построении непараметрической оценки (1) на основе выборки, сформированной по бутстреп-методу, – 1,5 % (рис. 14).

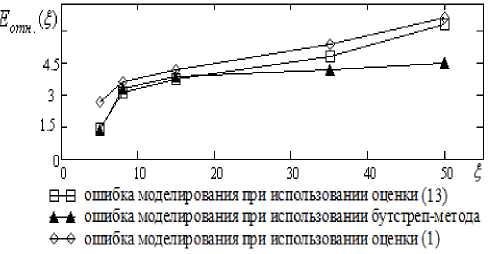
Рис. 14

Анализ графиков на рис. 14 позволяет сделать вывод, что при сравнительно малом уровне помехи в каналах измерения выходного сигнала (< 15 %) наименьшую ошибку моделирования дает модифицированная оценка регрессии (13). При увеличении уровня шума (> 15 %) ошибка моделирования на основе бут-стреп-метода становится меньше, чем при использовании оценки (13). Следует отметить, что при высоком уровне помехи в каналах измерения (> 40 %) качество построения модели при помощи модифицированной оценки (13) становится практически эквивалентным качеству моделирования на основе стандартной непараметрической оценки (1).

Сравним результаты численного моделирования при использовании модифицированной оценки регрессии (13) в случае, когда функция локальной аппроксимации ф j ( и ) = Р _{2 j}и ² + Р 1 _jи + Р ₀ j , j = 1, s , имеет квадратичный вид, и в случае, когда она линейна: ф j ( и ) = Р 1 j И + ₽ 0 j , j = 1, s .

Пусть имеется неравномерная выборка наблюдений одномерных входного и выходного воздействий объекта ( и , , x , ), г = 1, s , объемом s = 20, и е (0;1), x = ф ( и ) + ^ , где ф ( и ) = sin(5 ■ и ); ^ - 30%-я центрированная помеха в каналах измерения выходного сигнала.

Оценка ошибки моделирования при использовании непараметрической оценки регрессии (13) с квадратичным аппроксимирующим полиномом ф j ( u ) = P 2 j u ² + P 1 j u + P 0 j , j = 1, s , в 1,1 раза меньше, чем с линейным полиномом ф j ( u ) = Р 1 j u + Р 0 j , j = 1, s . При дальнейшем увеличении порядка полинома ошибка моделирования практически не изменяется, а при порядке полинома больше четырех ошибка моделирования увеличивается. Таким образом, предлагается использовать второй порядок аппроксимирующего полинома ф j ( u ), j = 1, s .

Представим зависимости оценок ошибки моделирования при использовании стандартной непараметрической оценки (1) на основе исходной выборки наблюдений и выборки, дополненной по бутстреп-методу, а также модифицированной оценки регрессии с квадратичным аппроксимирующим полиномом от уровня шума, % (рис. 15).

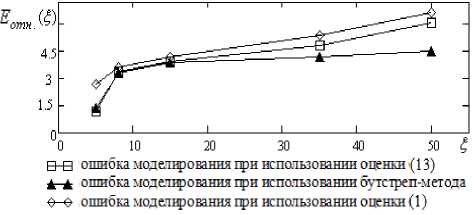
Рис. 15

Таким образом, разработанные методы построения непараметрических моделей позволяют довольно эффективно моделировать объекты в случае неравномерно распределенной выборки наблюдений входных и выходных воздействий. Применение несимметричной колоколообразной функции способствует большей согласованности модели и объекта по сравнению с симметричной функцией. Однако при увеличении размерности входной переменной на единицу время расчета модели при использовании модифицированной оценки регрессии (13) с несимметричной коло- колообразной функцией увеличивается в среднем в 1,5 раза при фиксированном объеме выборки наблюдений.

В заключение дадим несколько рекомендаций по применению представленных оценок в различных условиях. В случае идентификации объекта на основе представительной выборки наблюдений можно использовать любую из предложенных оценок. При наличии пустот в пространстве наблюдений и малом уровне помехи в каналах измерения для моделирования больше подходит модифицированная оценка регрессии (13) с несимметричной колоколообразной функцией и квадратичным аппроксимирующим полиномом. Если в каналах измерения высокий уровень помех, то предлагается использовать непараметрическую оценку, построенную на основании дополненной по бутстреп-методу выборки наблюдений.