О непараметрической идентификации частично-параметризованного дискретно-непрерывного процесса

Введение. Для многих технологических, производственных, многомерных процессов дискретно-непрерывного характера во многих случаях исследователь находится в условиях, когда необходимо построить модель исследуемого процесса. Это процессы динамические по своей природе, но контролируемые через дискретные интервалы времени, в том числе различные. Это приводит к тому, что динамические по своему характеру процессы должны рассматриваться как безынерционные с запаздыванием. Например, при измельчении каких-либо материалов (клинкер, уголь) постоянная времени составляет 5-10 мин., а контроль выходной переменной, например, тонкость измельчения, измеряется раз в два часа. В этом случае исследуемый процесс можно представить как безынерционный с запаздыванием [1].

Такие процессы часто встречаются в добывающих или перерабатывающих отраслях промышленности, например, в металлургии (плавка стали), энергетике (горение угля), стройиндустрии (получение цемента), нефтепереработке (процесс очистки дизельного топлива) [2], а также в социальных науках, включая образовательный процесс (получение знаний студентами) [3].

Но самым интересным и важным является то, что на пути исследования различных процессов выделен такой класс процессов, которые отнесены к Т-процессам [1]. Подобные процессы имеют стохастическую зависимость выходных переменных и требуют другие методы идентификации и управления, несколько отличающиеся от общепринятых. Главное здесь состоит в том, что идентификация подобных объектов должна осуществляться не традиционным для существующей теории идентификации путем [4]. Также интересен случай, когда априорная информация соответствует одновременно как непараметрическому, так и параметрическому типу исходных данных об исследуемом процессе. Такие процессы отнесены к КТ-процессам [1].

Особенностью КТ-процессов является то, что по одним каналам многомерной системы известны уравнения зависимостей входных и выходных переменных с точностью до вектора параметров, а по другим не известны такие уравнения. Данная постановка вопроса приводит к тому, что математическое описание объекта представляется в виде некоторого аналога системы с частично параметризованными F .( и , x , а ) = 0, j = 1, n и неизвестными функциями вида Fj ( u , x ) = 0, j = 1, n . Таким образом, задача идентификации сводится к задаче решения системы нелинейных уравнений частично параметризованного дискретно-непрерывного процесса относительно компонент вектора x = ( x_x , x ₂,..., x_n ) при известных значениях входных переменных и . Конкретные задачи идентификации будут отличаться различными объемами априорной информации по различным каналам, особенностью протекающих процессов. Здесь важным является то, что приходится сталкиваться с системой разнотипных, с точки зрения математики, уравнений, решение которых будет требовать развитие специальных методов. В этом случае целесообразно использовать методы непараметрической статистики [5; 6].

КТ-процессы. В данное время повышается роль идентификации безынерционных систем с запаздыванием [7; 8]. Это объясняется тем, что измерение некоторых, наиболее важных выходных переменных динамического объекта осуществляется через большие промежутки времени, значительно превосходящие постоянную времени объекта.

Рассмотрим общую схему дискретно-непрерывного процесса, который функционирует в условиях разнотипной априорной информации, в том числе в условиях непараметрической неопределенности, что соответствует теории идентификации в широком смысле.

Особенностью идентификации многомерного объекта является то, что исследуемый процесс описывается системой с неявными стохастическими уравнениями.

F j ( u ( t - т ), x ( t ), ^ ( t ) ) = 0, j = 1, n , (1) где по некоторым каналам F ( • ) - не известны, а по другим каналам известны, т -запаздывание по различным каналам многомерной системы [1]. В дальнейшем, из соображений простоты, т будет опущено.

В общем виде исследуемая многомерная система, реализующая КТ-процесс, может быть представлена на рис. 1.

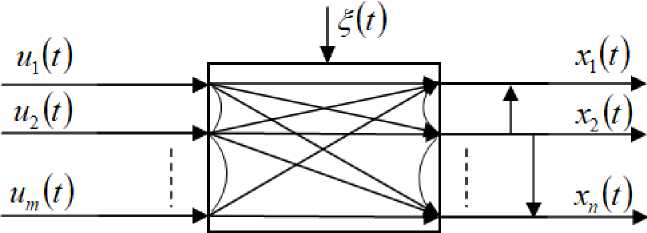
Рис. 1. Многомерная система

Fig. 1. Multidimensional system

На рис. 1 приняты следующие обозначения: u = ( u_x ,..., u_m ) - m-мерный вектор входных переменных; x = ( x_x ,..., x_n ) - n-мерный вектор выходных переменных; ^ ( t ) - случайные помехи, действующие на процесс; вертикальные стрелки обозначают стохастическую зависимость выходных переменных; стрелки-дуги означают внутреннюю связь между переменными, свойственные конкретному исследуемому процессу. Естественно, характер некоторых связей остается неизвестным исследователю.

По различным каналам исследуемого процесса зависимость j -й компоненты вектора x может быть представлена в виде некоторой зависимости от тех или иных компонент вектора u : x < ^j > = f.(u < ^j > ) j = 1, n . Подобные функции определяются исследователем на основании имеющейся априорной информации и называются составным вектором. Составной вектор – это вектор, составленный из некоторых компонент соответствующего вектора, в частности u < ^j > = ( x ₂, x ₅, x ₇, x ₈) . Также это может быть любой другой набор, например u < ⁵ > = ( u_x , u ₃, u ₆) , где u < ⁵ > означает составной вектор, или x < ³ > = ( u_x , u ₃, x ₂) . В этом случае система уравнений примет вид:

F i (u ^<  j > , x ^<  j >  , а ) = 0,

F 2 \,и < ^j > , x < ^j > , a ) = 0,      _

« ...                           j = 1, n ,                                       (2)

F n — 1 ( u "^j> , x ^{< j} > ) = 0, _ F_n (u "  j > , x <  j > ) = 0.

где F₃ ( • ) частично параметризованы либо неизвестны; а - вектор параметров.

КТ-модели. Многомерные процессы, выходные переменные которых имеют неизвестные стохастические связи, были названы Т-процессами, а их модели, соответственно, Т-моделями [1]. К-модели базируются на использовании разнотипной априорной информации по различным каналам многомерного объекта. КТ-модель объединяет элементы Т-модели с элементами К-модели и представляет собой модель, в которой есть совокупность взаимосвязей входных и выходных переменных, причем по одним каналам они известны, например, ориентируясь на законы физики, а по другим каналам зависимости неизвестны.

Основной особенностью моделирования подобного процесса в непараметрической неопределенности является тот факт, что вид Fj(u,x) = 0, j = 1,n известен по одним некоторым каналам и неизвестен условиях функций по другим.

Естественно, что система моделей может быть представлена в следующем виде:

F ( u < ^j > , x < ^j >  , a ) = 0;

F ₂ ( u ^<  j > , x^< j >  , a ) = 0;

« ...                            j = 1 n ,

F n - i ^{( u} < ^J > , x < ^j > , x s , ^us ⁾⁼ 0;

_ F , ( u < j > , x < j > , x s , u s ) = 0.

где x_s , u_s - временные векторы (набор данных, поступивший к s -му моменту времени), в частности x_s = ( x 1 ,..., x_s ) = ( x _H, x ₁₂,..., x 1 _s ,..., x ₂₁, x ₂₂,..., x ₂ s ,..., x_{n 1}, x_{n 2},..., x_ns ) , но и в этом случае некоторые F ( • ), j = 1, n остаются неизвестными. Поэтому рассмотрим задачу построения КТ-моделей в условиях непараметрической неопределенности, т. е. в условиях, когда система (3) известна по некоторым каналам и не известна с точностью до параметров по другим.

Итак, пусть на вход объекта поступают входные переменные, значения которых измерены. Наличие обучающей выборки xt,ut, i = 1,s необходимо. В этом случае оценка компонент вектора выходных переменных x при известных значениях u , как уже было отмечено выше, приводит к необходимости решать систему уравнений (3). В случае если зависимость выходной компоненты от компонент вектора входных переменных не известна, то естественно воспользоваться методами непараметрического оценивания [9; 10].

Задача сводится к тому, что при заданном значении вектора входных переменных u = u' , необходимо решить систему (3) относительно вектора выходных переменных x . По некоторым каналам многомерной системы, по которым известны уравнения с точностью до параметров, коэффициенты находятся, например, методом стохастических аппроксимаций [11]. По остальным каналам, где неизвестны уравнения, необходимо применить следующую алгоритмическую цепочку [1]. Сначала вычисляются невязки по формуле:

E ij = F j ^{( u} <  j >  , x <  j >^{( i} ^ x s , ^u s ) ^j = ¹ n , ⁽⁴⁾ где F ( u < ^j > , x < ^j > (i ), x_s , H_s ) примем в виде непараметрической оценки регрессии Надарая -

Ватсона [12]:

^£ jk i ) = F j ^{( u} < j > , x j ^{( i} ) ) = ^xj ^{( i )-}

s         <  n >

X x j [ i ] П Ф

i = 1          k = 1     ^

^u k - ^uk ^[ i ^]

c su_k

s <  n >

ХП Ф i=1  k=1

' ^u k ^{- u}k ^[ i ^]

V

suk

где j = 1, n, , < m > - размерность составного вектора uk . Колоколообразные функции фf uk - uk [i 1'

V     c ^su k      у

и параметр размытости c

удовлетворяют некоторым условиям сходимости и

обладают следующими свойствами:

Ф(-) < то; cs1 J Ф(cs1 (u - u ))du = 1;(6)

Q ( u )

lim s^ с-1ф(c-1 (u - ui ^ = 5(u - ui ), lim s^ cs = 0, lim s^ scs w .

Следующий шаг состоит в оценивании условного математического ожидания:

Xj = M {x | u , £ = o}, j = 1, n .(8)

В качестве оценки (8) примем непараметрическую оценку регрессии Надарая – Ватсона [12]:

~

x

5^    p.-, T n T ,^f u k,    u k , ^[ i ¹ ) < m f i^{f £} k ₂ ^[ i ¹

E х[ i]-П ф —:--П ф — i=1          k 1 =1 V      csu      У k 2 =1 V cs£ У

s <  n >

' ^uk 1

i = 1 k ₁ = 1 V

u k , ^[ i ¹ ^ T m f Л ^£ ki ^[ i ¹

~— Пф csu      Jk 2 =1   V cs£ У

j = 1, n ,

где колоколообразные функции Ф ( - ) могут быть взяты в виде треугольного ядра (10) и (11), и удовлетворяют условиям (6), (7).

ф

f u_k - u_k [ i 1 ) ф jk

V     csu     J f £k2[i11

V   c s £  J

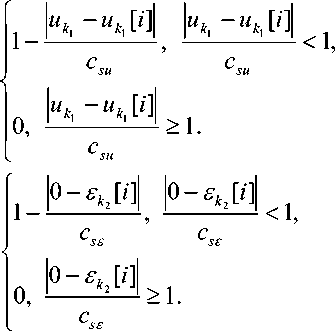
Алгоритмы (5), (8) и (9) представляют собой алгоритмическую цепочку, необходимую для вычисления прогноза компонент вектора выхода при известных компонентах входа [1].

Осуществляя эту процедуру, получаем значения выходных переменных x при входных воздействиях на объект u = u' (а в этом и состоит основное назначение искомой модели), которые в дальнейшем могут быть использованы в различных системах управления [9], в том числе в организационных системах [3].

Точность моделирования оценивается по следующей формуле:

еЕ х - x s ( u , )

5 = ^J=^L s ----------,                                  (12)

Elx- x i=1

где Xj - наблюдения на объекте; x₅ (u_t ) - прогноз выхода объекта; x - среднее значение по каждой компоненте вектора x .

Вычислительный эксперимент. Для вычислительного эксперимента был взят объект с пятью входными переменными u = (ux, u2, u3, u4, u5) и тремя выходными переменными x = (x,, x2, x3). Для данного объекта была сформирована выборка входных и выходных переменных, исходя из системы уравнений из двух параметрических и одного непараметрического каналов. В результате была получена обучающая выборка й$, xs, где us, xs - временные векторы. Если бы задача решалась для реального объекта, обучающая выборка формировалась в результате измерений, осуществляющихся имеющимися средствами контроля. В случае стохастической зависимости между выходными переменными процесс естественно описать, например, следующей системой уравнений:

^Fx i ^{( x} i , ^x з , u i , u 2 , u 5 ) = °;

< F x ₂ ⁽ x i , x _г, u ₄, u 5 ) = °;                                            (1³)

F x 3 ( x i , x 2 , x 3 , u 2 , u 3 , u 5

) = °-

После того, как была получена выборка наблюдений, можно приступать к исследуемой задаче - нахождению прогноза значений выходных переменных x при известных входных u. Для случая, если по двум каналам имелась зависимость в виде уравнений, коэффициенты были найдены с помощью метода стохастических аппроксимаций.

Для начала вычисляются невязки по методике, описанной ранее. Представим невязки в виде системы:

^ i ( i ) = F i ( x i , x 3 , u l , u 2 , u 5 )

" ^S 2 ^{( i} ) = ^F2 ⁽ x i , x 2 , u 4 , u 5 ^

(i4)

S 3 ( i ) = F 3 ( x i , x 2 , x 3 , u 2 , u 3 , u 5

где Sj , j = i,3 - невязки, соответствующие компоненты вектора выхода которых не могут быть выведены из параметрических уравнений.

Прогноз для системы (13) осуществляется согласно формуле (9) для каждой компоненты выхода объекта.

На вход объекта подаются значения входных переменных вновь сгенерированных входных переменных, т. е. не входящих в обучающую выборку. Настраиваемым параметром будет параметр размытости с$, который в данном случае возьмем равным 0,4 (значение было определено в результате многочисленных экспериментов с целью уменьшения квадратичной ошибки между выходом модели и объекта [i3; i4], параметр размытости примем одинаковым при подсчете в формулах (5) и (9), объем выборки 5 = 2°°°, помеха £ = °,°7 . По компонентно приведем графики для выходов объекта x , x и x .

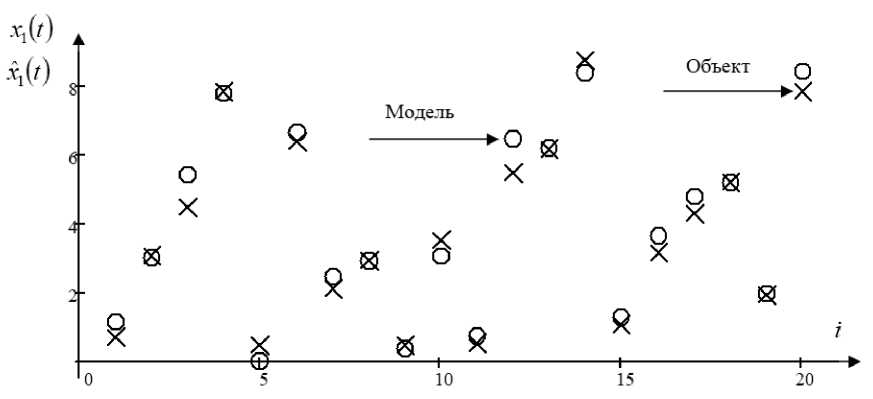
Рис. 2. Прогнозные значения выходной переменной x при помехе 7 %

Fig. 2. Forecast values of the output variable x 1 with interference 7 %

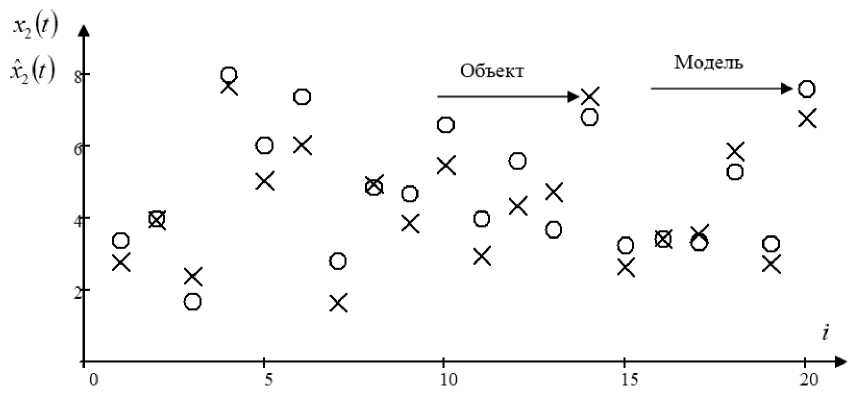
Рис. 3. Прогнозные значения выходной переменной x при помехе 7 %

Fig. 3. Forecast values of the output variable x 2 with interference 7 %

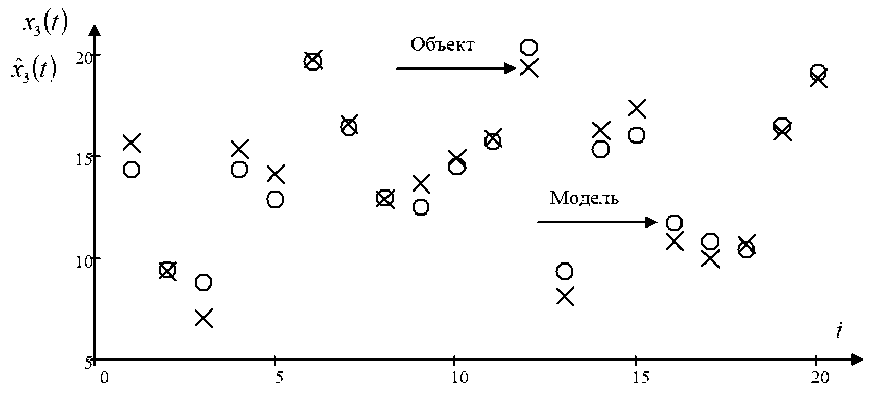
Рис. 4. Прогнозные значения выходной переменной x при помехе 7 %

Fig. 4. Forecast values of the output variable x 3 with interference 7 %

На рис. 2–4 «крестиком» обозначены значения выхода переменных, а «точкой» значения выхода модели; продемонстрировано сравнение истинных значений тестовой выборки компонент вектора выхода и их прогнозные значения, полученные при помощи алгоритма (5) – (9); представлены 20 точек выборки из-за простоты представления результатов, т. е. каждая сотая точка выборки. На рисунках видно, что модель достаточно хорошо описывает объект при помехе 7 %, действующей на компоненты выходных переменных. На рис. 3 прогноз выходной переменной x несколько хуже, чем по остальным выходным переменным, на это может влиять качество обучающей выборки, зависимость переменных, случайные помехи, параметры размытости и т. д.

Заключение. В данной работе была рассмотрена задача идентификации частично параметризованных многомерных объектов с запаздыванием. Здесь возникает ряд особенностей, которые состоят в том, что задача идентификации рассматривается в условиях непараметрической неопределенности и, как следствие этого, не может быть представлена с точностью до набора параметров. Такие процессы могут быть хорошо использованы в различных системах управления [15]. На основании имеющихся априорных гипотез выписывается система уравнений, описывающих процесс с помощью составных векторов x и u . Но функции F ( • ) продолжают оставаться неизвестными по некоторым каналам. В статье рассмотрена методика расчета выходных переменных объекта при известных входных, что позволяет их использовать в компьютерных системах различного назначения.

Также необходимо отметить, что КТ-модели нашли свое применение для реального процесса каталитической гидродепарафинизации (или процесса очистки дизельного топлива) и в результате проведения вычислительных экспериментов дали достаточно удовлетворительные результаты [2].

Проведенные многочисленные вычислительные эксперименты показали достаточно удовлетворительные результаты КТ-моделирования. При этом исследовались вопросы, связанные с введением различных помех, разных объемов обучающих выборок, но и объектов различных размерностей [4].