О непараметрической оценке нестационарной функции регрессии по наблюдениям

В многочисленных приложениях часто возникает необходимость в восстановлении функции регрессии М { x | u } по наблюдениям случайных величин ( ui , xi ), i = 1, 5 , где 5 - объем выборки наблюдений. В классе непараметрических оценок принята статистика, которая будет представлена далее [1]. Предполагается, что плотность вероятности p ( u ), V u , u е Q ( u ), p ( и ) > 0 неизвестна. При этом предполагается, что x ( u ) не меняется с течением времени. Поскольку при моделировании дискретно-непрерывных процессов широко используются регрессионные модели, то существенное значение имеет факт дрейфа во времени характеристик исследуемого объекта. Среди многих факторов, влияющих на последнее, отметим только безусловное старение оборудования, других технических средств, где и протекает интересующий нас процесс. Однако укажем кратко и на другие причины, влияющие на дрейф характеристики процесса, а также отметим некоторые его проявления при моделировании:

– наличие неизвестных переменных либо переменных, не поддающихся измерению (естественно, что для успешного решения задачи идентификации с присутствием неконтролируемых входных переменных процесса их значения должны меняться медленно; в противном случае, и тем более, когда значения таких переменных случайны и приводят к осциллирующему процессу, ожидать хороших моделей не приходится);

– изменение параметров модели объекта во времени (речь в данном случае идет не об изменении параметров модели, как это происходит в ряде рекуррентных алгоритмов идентификации, когда наблюдается сходимость параметров некоторым оценкам, а о дрейфе параметров, связанных именно с изменчивостью объекта идентификации);

– изменение структуры объекта во времени (редко встречающаяся на практике ситуация, тем не менее, интересная с точки зрения теории, побуждающая к построению более универсальных, адаптивных алгоритмов идентификации).

Приведем примеры изменения характеристики нестационарного процесса. Из соображений простоты рассмотрим одномерные статические объекты (рис. 1). На рис. 1, а и 1, в представлены истинные характеристики стационарного и нестационарного объекта. Характеристика последнего изменилась за некоторый интервал времени [t1, t2]. Точки выборки, полученные с обоих объектов, показаны на рис. 1, б и 1, г. Объемы выборки наблюдений одинаковы, на выход объекта наложена одинаковая аддитивная центрированная помеха.

На рис. 1 приняты следующие обозначения: u – входная переменная процесса; x – выходная переменная. Приведенная иллюстрация, помимо разъяснения, о каких процессах идет речь, подводит к следующей задаче: необходимо определить, имеем ли мы дело со стационарным процессом и присутствуют ли помехи в каналах измерений, или имеющаяся выборка отражает поведение нестационарного процесса, а не просто несет в себе искажения, вносимые помехами измерений.

Далее рассмотрим непараметрические оценки функции регрессии по наблюдениям при неизвестном дрейфе изучаемого процесса.

Непараметрические оценки функции регрессии. Непараметрическая оценка функции регрессии по наблюдениям с ошибками {xi, u(1)i, u(2)i, …, u(m)i}, i = 1,5, где m - размерность вектора входных переменных, имеет вид [1; 2]

x s ⁽ « 1 ,-, u m ) =

, где финитная колоколообразная функция Ф0 удов- летворяют некоторым условиям сходимости [2]:

lim— ф ( ( u - u i ) / c_s ) = 8 ( u - u i ),

5 ^” C    '

— J Ф ( ( u - u i ) / c_s ) du = 1,            (2)

c s П ( u )

где δ( u – u_i ) – дельта-функция Дирака. Параметр размытости cs удовлетворяет следующим условиям сходимости [1; 2]:

c_s >  0, lim c_s = 0, lim s ■ c_s™ =^ .       (3)

s ^^         s ^^

Асимптотические свойства непараметрической оценки (1) достаточно хорошо исследованы, в частно- сти, сходимость оценки xs доказана в среднеквадратичном и почти наверное [3; 4]. Однако эта непараметрическая оценка (1) непригодна для восстановления регрессионных характеристик нестационарного объекта.

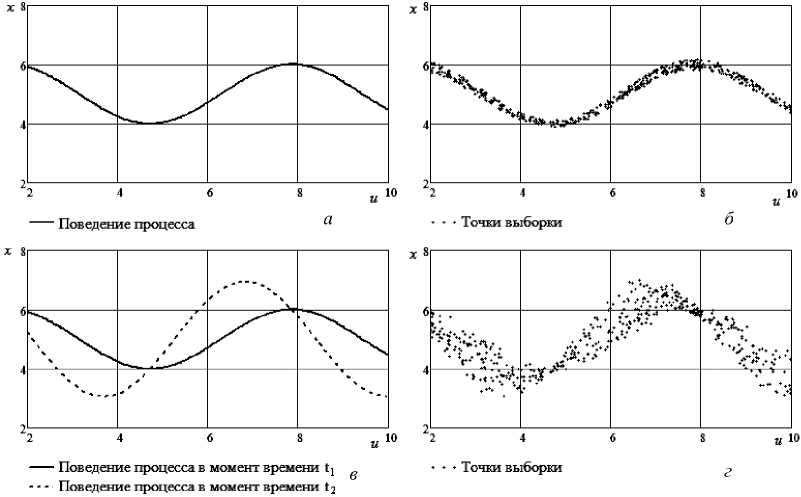
Рис. 1

Нестационарная непараметрическая оценка функции регрессии. Пусть истинная характеристика процесса изменяется во времени в пространстве входных и выходных переменных заранее непредвиденным образом. В этом случае использование всей выборки наблюдений, проводимых в оценке (1), будет искажать оценку функции регрессии, и обусловлено это будет тем, что наблюдения, ранее полученные на объекте, не отражают свойств объекта в настоящий момент времени. Естественно считать, что «старая» информация в виде элементов выборки { xi , u ⁽¹⁾ i , u ⁽²⁾ i , …, u ^{( m )} i , I = 1, 2,...} должна использоваться с меньшим весом.

Идея непараметрического алгоритма, учитывающего временной дрейф характеристик исследуемого процесса, состоит в том, что «старая» информация в непараметрической оценке функции регрессии получает меньший вес [2].

Для восстановления функции регрессии в нестационарных условиях x ( u , t ) предлагается ввести в непараметрическую оценку функции регрессии (1) некоторую функцию «памяти», убывающую с увеличением аргумента ρ = ( s–i ), где i – дискретное время поступления информации, I = 1, 2, … s ; s – текущее время [2]. Тогда непараметрическая оценка нестационарной функции регрессии по наблюдениям ( x , u ) будет иметь вид

• 2)    V i , j e [1, s ], i >  j ^p ( s - i ) >p ( s - j );

• 3)    i = 1 ^ p ( s - i ) = p ( s - 1) >  0 .

Приведем варианты вида функции памяти ρ( s – i ):

p ( s - i , a_p a ₂ )

-(s - i) + a1

| ( s - i ) - C 11 + a 2

0,5 + 0,5

a ₂ ,

a ₃ =

0,5 -a 1

a1 +a2

^{+ 0,5},

где параметр a 1 e (0, s ) определяет положение точки перегиба функции; параметр a₂ e (0, » ) определяет «крутизну» функции; параметр α 3 нормирует функцию «памяти» на единицу. Поведение функции (5) (функции «памяти») при различных значениях параметров α₁ и α₂ приведено на рис. 2.

Также функция «памяти» может быть кусочнопостоянной, приводя к скользящему аналогу непараметрической оценки (1).

Введем показатель изменчивости 5 ( 1 1 , 1 ₂) характеристики исследуемого процесса в следующем виде:

5 ( t 1 , 1 ₂ ) = j | x ( u , t 1 ) - x ( u , 1 ₂ )| du .        (7)

Q ( u )

( jj - jj A

Z x i П ^ф| —I p ( ^s - i )

*                           i=1          j=1

xX И,,..., um ) = ---—---^----p---------,(4)

smj j

2П ф|       |P ( s - i )

i=1 j=1    V Cs)

где ρ = ( s–i ) – функция «памяти», удовлетворяющая следующим свойствам:

1) i = S ^p ( s - i ) = p (0) = 1;

Обозначим дискретность измерения переменных ( x , u ) через A t . Величина A t , естественно, будет зависеть от показателя изменчивости 5 ( 1 1 , 1 ₂), где 1 1 <  1 ₂. Можно считать, что при медленно меняющейся во времени характеристике процесса, т. е. при малых значениях 5 ( 1 1 , 1 ₂), дискретность измерений A t «вход-ных–выходных» переменных процесса ( x , u ) больше, чем в случае больших значений 5 ( 1 1 , 1 ₂). В последнем случае параметр A t - дискретность измерения «вход-ных–выходных» переменных, следует уменьшить. Анализ этого вопроса требует дополнительных исследований имеющейся выборки наблюдений { xi , u ⁽¹⁾ i , u ⁽²⁾ i , …, u ^{( m )} i , I = 1, 2, ...}.

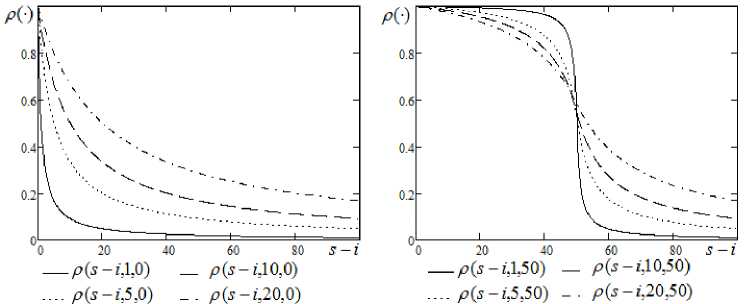
Рис. 2

Другой подход к попытке оценить изменчивость исследуемого процесса состоит в выявлении подобластей в пространстве входных и выходных переменных, которые могут отражать нестационарность процесса. Он основан на применении условной дисперсии D { x | u } = M { x ²| u } – [ M { x | u }]² [5]. Условная дисперсия выходной переменной может быть оценена следующей непараметрической статистикой:

указание учителя о принадлежности S к классу V ₁ или V ₂. В этом случае модификация непараметрического алгоритма классификации, учитывающая изменчивость классов, имеет вид

U s ( v 1

^D s ⁽ x I u ) =

s

2 xi i =1

m

П Ф

. j = 1

u j - u j c_s^j

-

-

s

2 X i i = 1

sm

2ПФ i =1 j =1

u j - u j c s ^j

m

П Ф

. j = 1

sm

2Пф i =1 j =1

u j - u ji c s ^j

_m_   ( j - j I

2Ui Пф| —I p(s-i) i=i    L j=i v cs    Л sm     j j

21 I'¹’             |p ( s - i )

i = 1 j = 1 v c s      J

Управление. Аналогичную предыдущей модификацию можно предложить и для непараметрического алгоритма управления статическим нестационарным объектом:

E ¹ ^1 X - Xi I ^ ф! ------Ip ( s - i )

i=1      V cs J us (X) = ^--^---S------,

E | x u^ | ф|------ ^L |p ( s - i ) i = 1 V c s J

Большие значения оценки (8) (к примеру, выше некоторого порогового значения) могут сигнализировать об изменчивости объекта в рассматриваемых подобластях пространства наблюдений.

Нестационарные адаптивные модели и алгоритмы. Рассмотрим нестационарные адаптивные модели.

Распознавание образов. Оценка (4) с использованием функции «памяти», помимо применения в задаче оценки нестационарной функции регрессии, также может применяться и к непараметрическим алгоритмам классификации, а необходимость в них возникает, когда обучающая выборка накапливалась в течение некоторого времени, за которое расположение классов в признаковом пространстве изменилось, при этом классические алгоритмы классификации, не учитывающее изменение классов во времени, естественно, будут давать плохие результаты.

Рассмотрим случай, когда некоторая ситуация S может быть отнесена к одному из двух классов V1 или V2 и характеризуется значениями вектора признаков v = (vi, ..., vs). Задача классификации сводится к построению решающего правила на основании обучающей выборки {vs = (v 1,..., vm),Us} объемом s, где Us - где x* – требуемое значение выхода объекта.

Статистическое моделирование нестационарных непараметрических оценок функции регрессии. При исследовании непараметрической оценки нестационарной функции регрессии (4), а также при сравнении результатов с использованием оценки (1) использовался метод статистического моделирования. В качестве уравнения, описывающего моделируемый объект, было выбрано следующее:

x(u,.) = sinu(1) +---cos u(2))- i i 250 i             (11)

- u*31 ■ u(4) + sin (u*51 + 0,5),

где i e [1, s ], s - объем выборки; u ⁽¹⁾ e [0,5], u ⁽²⁾ e [0,5], u ⁽³⁾ e [0,5], u ⁽⁴⁾ e [0,5], u ⁽⁵⁾ e [0,3]. Значения входных переменных u генерировались случайно в соответствии с равномерным законом распределения в заданных интервалах.

Для имитации функционирования объекта в условиях помех различной интенсивности на имитируемый выход объекта (11) накладывается центрированная аддитивная помеха по следующему правилу:

Xi = x * +^- , (12)

где x_i – выход объекта с наложенной на него помехой; x_i ^* – выход объекта без помехи; ξ – случайная величина, подчиняющаяся нормальному закону распределения N (0, σ), а значение среднеквадратичного отклонения σ определяется в зависимости от заданного уровня помехи e (%) согласно выражению

[ max( x ( u | i = 0), x ( u | i = 5 )) - e

( - min( x ( u 1 1 = 0), x ( u 1 1 = 5 )) CT =--------------------------------------------^:

6 - 100%

в этом случае интервал 6σ будет соответствовать заданному в процентах интервалу от изменения выхода объекта.

Оценка качества моделирования проводилась с использованием следующего критерия:

1 ^s                                2

^W =    - Ё ( x ⁽ ut ) - xs ⁽ u l , c 5 )) ,      ⁽¹⁴⁾

V ⁵ t =1

где x ( ul ) – значение выходной переменной в l -й точке выборки в момент времени s ; x_s ( u_l , c_s ) – значение выхода модели (1), построенной по имеющейся выборке в той же точке. Аналогично будем проводить оценку качества моделирования при использовании непараметрической модели (4):

1s2

W =    'E( x(ul ) - xs (ul , cs )) ,

V 5 t=1'

где x_s ^* ( u_l , с_s ) – значение выхода оценки (4).

Оценку ошибок моделирования по нескольким экспериментам, проводимым в одних и тех же условиях, будем проводить усреднением по серии экспериментов.

Результаты исследования качества моделирования в зависимости от уровня шума е (%) приведены в табл. 1, усреднение проводилось по 50 экспериментам при каждом уровне шума, объем выборки s = 3 000.

Сравнение зависимости среднеквадратичных оценок ошибок моделирования (14) и (15) для стандартной (1) и модифицированной (4) непараметрических оценок функции регрессии от уровня шума e (%) приведено на рис. 3.

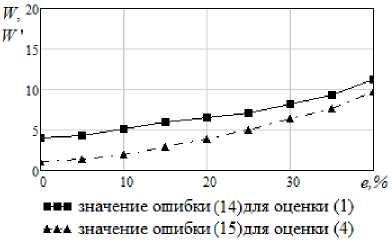
Рис. 3

Можно сделать вывод, что исследуемый алгоритм чувствителен к помехам, а также к точкам выбросов, ввиду того, что больший вес придается последним наблюдениям, даже если они оказываются ошибочными.

Приведем результаты моделирования при увеличении объема выборки за счет уменьшения шага дискретизации снятия наблюдений. То есть увеличим число наблюдений при условии, что последнее наблюдение будет происходить при одинаковых параметрах объекта (табл. 2). Усреднение проводилось по 50 экспериментам при каждом объеме выборки, на выход объекта наложена 5%-я помеха.

Графически сравнение зависимостей среднеквадратичных ошибок моделирования (14) и (15), указанных в табл. 2, представлено на рис. 4.

Как видно из рис. 4, при уменьшении шага дискретизации снятия наблюдений по времени (а в данном случае именно за счет этого увеличивался объем выборки) заметна некоторая сходимость модифицированного алгоритма (4).

Увеличим объем наблюдений, оставив шаг дискретизации снятия наблюдений постоянным, сохранив исходный характер нестационарности (11). Объем выборки наблюдений s будет равен 3 000, 5 000, 7 000, 9 000, 12 000. Результаты приведены в табл. 3.

Сравнение зависимостей относительных ошибок моделирования (14) и (15) для стандартной и модифицированной непараметрических оценок функции регрессии по проведенной серии экспериментов представлено на рис. 5.

Таблица 1

Значение усредненных оценок ошибок моделирования в зависимости от уровня помех

e , %	0	5	10	15	20	25	30	35	40
W	4,08683	4,35962	5,1858	5,97146	6,50943	7,11131	8,16638	9,34669	11,26575
W’	1,10454	1,42067	1,91831	2,9245	3,90674	4,93265	6,40269	7,70785	9,69883

Таблица 2

Значение усредненных оценок ошибок моделирования в зависимости от объема выборки

s	3 000	5 000	7 000	9 000	11 000	20 000
W	4,35962	4,35114	4,28764	4,25306	4,20386	4,18571
W’	1,42067	0,71623	0,30293	0,15271	0,14397	0,11291

Таблица 3

Значение усредненных оценок ошибок моделирования в зависимости от объема выборки

S	3 000	5 000	7 000	9 000	12 000
отн	4,35962	5,65906	8,00766	11,24024	17,08449
Е* отн	1,42067	1,56532	1,62685	1,7869	2,05778

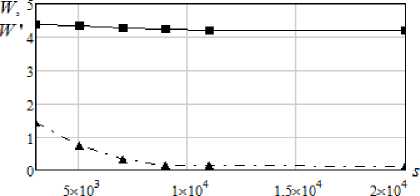
■■■ значение ошибки (14)для оценки (1)

*и значение ошибки (15)для оценки (4)

Рис. 4

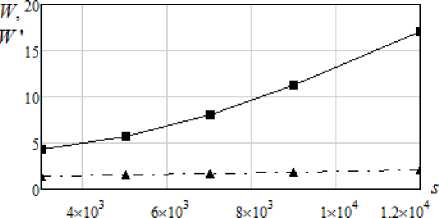
■■■ значение ошибки (14) для оценки (1)

*** значение ошибки (15)для оценки (4)

Рис. 5

Последний рисунок, отражает наиболее существенный момент, отмеченный ранее: непараметрическая оценка (1) непригодна для восстановления регрессионных характеристик нестационарного объекта.

В ходе численных исследований определено, что использование предлагаемой непараметрической оценки нестационарной функции регрессии дает более точные результаты оценивания, чем известная непараметрическая оценка, кроме случаев с большим значением помехи. Рассматриваемый алгоритм более чувствителен к помехам.

Однако в любом случае адекватность получаемой модели зависит от реального объекта, скорости изменения характеристик объекта, частоты дискретизации снятия наблюдений, наличия априорной информации и качества получаемых данных.

При исчерпывающей выборке наблюдений позволительно использовать лишь ее часть для получения более точных оценок. Предлагаемый вид функции «памяти» рекомендуется использовать в тех ситуациях, когда невозможно определить вес каждого наблюдения конкретно. В противном случае, необходимо видоизменять функцию «памяти» в соответствии с имеющейся информацией.