О непараметрическом моделировании многосвязных процессов

This article publications cycle devotes to a new part of control theory. Nonparametric control systems theory is focused on the lower size of a priori information that differs itfrom the standard parametric control theory. The parametric theory assumes the stage of investigation process model to within to the vector ofparameters choosing, but nonparametric one requires data of process characteristics quality properties. It is principally different.

Д. А. Игнатьев, А. В. Медведев, Д. В. Сергеев, А. И. Шестернев

О НЕПАРАМЕТРИЧЕСКОМ МОДЕЛИРОВАНИИ МНОГОСВЯЗНЫХ ПРОЦЕССОВ

Рассматривается задача идентификации многосвязных процессов в условиях, когда параметрическая структура некоторых связей выходных и входных переменных известна или определена, а для восстановления других используется непараметрическая статистика. В этом случае комбинированная непараметрическая модель процесса представляет собой взаимосвязанную систему стохастических соотношений как параметрического, так и непараметрического типов. Приводятся комбинированные непараметрические модели.

Во многих практических задачах возникает необходимость построения модели достаточно сложного комплекса, состоящего из большого числа локальных объектов, объединенных в многосвязную систему. Многосвязным называется объект, состоящий из некоторого количества взаимосвязанных подсистем, которые описываются некоторой системой неявных функций от входных и выходных переменных.

При моделировании разнообразных дискретно-непрерывных процессов в настоящее время доминирует теория идентификации в узком смысле. Ее содержание состоит в том, что на первом этапе каким-то образом определяется параметрический класс операторов В, например, vo=*₽(«(ox'u₽), (1) а на втором этапе осуществляется оценка параметров в на основе имеющейся выборки

{ х, , u, , ц t , t = 1, У } ^, где s - объем выборки.

Успех решения задачи идентификации в этом случае существенно зависит от того, насколько удачно определен оператор (1).

Идентификация в широком смысле предполагает отсутствие этапа выбора параметрического класса оператора (1), если, конечно, для этого нет достаточных априорных сведений. Часто оказывается значительно проще определить класс операторов х(?) = Bluf\\ff,f на основе сведений качественного характера, например, линейности процесса или типа нелинейности, однозначности либо неоднозначности и др. В этом случае задача идентификации состоит в оценивании этого оператора на основе выборки.

В данной работе речь пойдет об описании исследуемого процесса с точки зрения идентификации в широком смысле.

Уровни априорной информации. Важную роль при решении задачи идентификации играет уровень априорной информации об исследуемом процессе. Априорная информация является необходимой для математической постановки задач, и в зависимости от ее уровня, методы решения задач оказываются различными.

Могут быть выделены следующие уровни априорной информации. По мере усиления неопределенности основная задача и ей сопутствующие могут быть рассмотрены при следующих уровнях:

• -    байесов уровень априорной информации, при котором информация об объекте может быть как полной (максимально возможной), когда точно заданы модель объекта, статистические характеристики наблюдений и возможных помех, так и неполной, когда вероятностные характеристики наблюдений, помех и вид модели известны с точностью до набора параметров;

• -    уровень параметрической неопределенности, при котором неизвестны законы распределения измерений и помех, а структура модели задана с точностью до набора параметров [1]. Присутствуют выборки статистически независимых наблюдений переменных объекта;

  -уровень непараметрической неопределенности, когда неизвестны ни законы распределения помех и измерений, ни структура модели. Известны некоторые качественные характеристики объекта: например, объект статический или динамический, однозначны или нет связи между его переменными и т. п. [2]. Имеются выборки статистически независимых наблюдений переменных объекта.

Многосвязные системы. Во многих практических задачах возникает необходимость построения модели достаточно сложного комплекса, состоящего из большого числа локальных объектов, объединенных в многосвязную систему.

Функционирование объекта происходит по схеме, приведенной на рис. 1.

Здесь u(t) e R ” - общем случае, векторные входное значение, включающее в себя входные переменные системы, промежуточные входы, являющиеся выходами других подобъектов и собственного выхода с запаздыванием; x(t) e R^m - векторное выходное значение, включающее в себя выходные переменные системы, промежуточные выходы, являющиеся входами для других подобъектов; u(t) и x(t) непрерывны во времени; h, h -случайные помехи, действующие в каналах измерений, с нулевым математическим ожиданием и ограниченной дисперсией; u^h [t], x^h [t] - входное и выходное значения, измеряемые в дискретные моменты времени; о(t) - случайная помеха, действующая на процесс. Помеха обусловлена «шумами» различных неконтролируемых факторов. «Шум» - некоторые воздействия, создаваемые окружающей средой и самой системой (рис. 2).

Рис. 1. Процесс функционирования подобъекта многосвязной системы

О ,

* о₂      ‘^|Л

hxX

Рис. 2. Помехи в каналах измерений

Здесь h^u2, h^vl и h^x1 - случайные помехи, действующие в каналах измерений величин v₂ и х_; соответственно; u₂^h [t], v₂^h [t] и x₁^h [t₁] - измерения с ошибкой, измеряемые с дискретностью dt и dy соответственно. В каждом канале связи системы можно выделить по помехе, т. е. h^u1, ..., h™, h^v1, ..., h^v14, h^x1, ..., h ”" . Исследователю доступны данные, измеренные с помехой.

Многосвязным называется объект, который описывается некоторой системой неявных функций от входных и выходных переменных.

Рассмотрим объект, имеющий вид многосвязной системы (рис. 3).

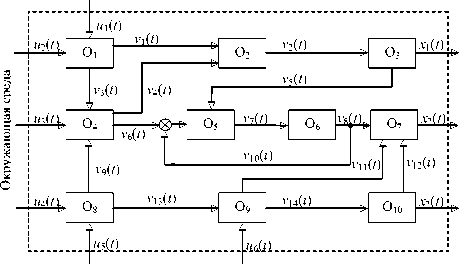
Рис. 3. Многосвязная система

Здесь О . - z-й подобъект многосвязной системы, z = 1, 2,..., 10; u . (t) - входные переменные, z = 1, 2, ..., 6; v . (t) - промежуточные переменные (как входные, так и выходные), z = 1, 2,..., 14;x . (t) - выходные переменные, z = 1,2,3; t-время. В каналах измерений (связи подобъектов) действуют случайные помехи, обозначим их через h (см. рис. 1), они могут быть обусловлены погрешностями приборов измерений, человеческим фактором и т. д. Термин окружающая среда подразумевает под собой среду, в которой система функционирует.

На практике достаточно сложно добиться равномерного и синхронного измерения параметров процесса. Общая схема измерений параметров процесса приведена на рис. 4.

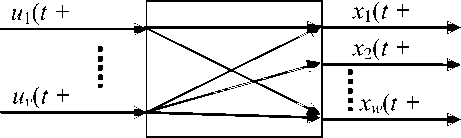
Рис. 4. Общая схема измерений параметров процесса

Переменные процесса измеряются с разной частотой Д/ и, соответственно, в различные моменты времени. В общем случае могут измеряться в один момент времени. Анализ таких данных весьма затруднителен, так как структура взаимосвязей переменных может оказаться достаточно сложной.

Математическая постановка задачи. Пусть имеется многосвязный объект. Измерения входных и выходных переменных представлены в виде векторов u_t = {u 1 , -, um } е R^m , x_t = { xt ¹ , ... , xl } e R^l , vt = { vt ¹ , ... , v" } e R" , t = 1, s .Вкана-лах измерений действует случайная помеха с нулевым математическим ожиданием и ограниченной дисперсией. Характеристики объектов Oj , j = 1...10 однозначны по вектору входных переменных. Имеется обучающая выборка { u_t , v_t , x_t , t = 1, s } . Необходимо построить математическую модель многосвязного стохастического объекта, адекватно описывающую его поведение при произвольном входном воздействии.

Сформируем критерий оптимальности:

R(x ) = М^и v) ^М_ (х‘ - х )2 | й, vJ = min, где х - оценка z-ой компоненты вектора выхода x ; u,v - совокупные векторы, составленные из компонент векторов u,v.

Используя необходимое условие минимума, т. е. приравняв производную функции R по искомой величине^ к нулю, получим:

• — opt _г -.

х = M { x | u, v } .

При построении математической модели исследуемого процесса следует выявить, к какому классу задач идентификации относится каждый из подобъектов многосвязной системы. Идентификация в узком смысле подразумевает построение модели в условиях байесового или параметрического уровня априорной информации. В первом случае необходимо лишь определить неизвестные параметры законов распределения и модели. Второй этап под- разумевает под собой определение параметров, а в некоторых случаях и виды законов распределения измерений. Итак, пусть объект описывается уравнением вида xi = F(ui,vi), i = 1,s, где x - выходное измерение объекта, и., v - входные измерения; F- функция процесса, преобразующая вектор входных значений в выходное.

Необходимо построить модель данного процесса, используя имеющуюся априорную информацию. Вид модели будет следующим:

Xi = F(ui,vi,a), i = 1,s, где Xi - оценка выхода процесса;/7 - оценка оператора F; a - вектор параметров процесса.

Также можно оценить параметры распределения переменных процесса, используя различные процедуры теории параметрической идентификации.

Если априорная информация отсутствует и имеются только измерения входных и выходных переменных, речь пойдет уже об идентификации в «широком» смысле. Модель объекта будет представлена в виде статистики [2; 3]

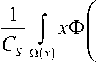
x - x i

S

d Q = x. .

J

случае, когда процесс является динамическим, мож

но воспользоваться следующими оценками:

xs (t) = ks (0) u (t) + jhs (t - t) u (t) d т для линейных систем, либо оценкой (2), где в качестве одной из компонент входа является сигнал обратной связи, для нелинейных систем

x , = £ x , Ф

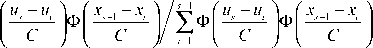
и,

= 1,5,

где S - непараметрическая модель процесса; м,, у - векторы значений входных переменных; Xi - непараметрическая оценка выхода. _ _

Непараметрическая оценка х ^₽ = х₍ равна следующей статистике по всем переменным (для статического процесса):

s -1

=£

i =1

m xi ^ПФ j =1

n х П Ф r =1

I v .r

X ui

^^^^^^.

^^^^^^.

v i^r

C ^j us

Cr usj

^j u_i

Существенный интерес, с точки зрения практики, представляет собой случай, когда для некоторых зависимостей компонент векторов x е R l , u е R m и v е R n известна их параметрическая структура с точностью до набора параметров a . В этой ситуации мы сталкиваемся с задачей идентификации, которая не соответствует ни параметрическому уровню априорной информации, ни непараметрическому. Такие модели возникают при описании сложных взаимосвязанных процессов (часто эта ситуация возникает при анализе производственных процессов с непрерывной технологией) и имеют вид взаимосвязанной системы:

x j = F j ( u^J , v ^j ) , j = 1, k , где индекс/при аргументах x_j , u^j , v ^j , a ^j -определенный (/-й) набор этих компонент из всех компонент соответственно векторов х, и, v, a ; F_j -j-й оператор процесса, переводящий вектор входных параметров в выходные; х - вектор выходных переменных; и, v - входных; a - параметров.

Модель многосвязной системы может быть представлена следующей системой уравнений [2; 3]:

s £ i =1

n х П Ф r =1

m xi "ПФ j =1

us

^^^^^^.

C ^j us

I v .r

^^^^^^.

v_i ^r

C ^r vs

^

, Х = 1, l ,

где Ф( - ) - колоколообразная функция, обладающая дующими свойствами:

сле-

x - x i

M

-1- [ф C_s -M

S

< A < m ,

s- j x - xi

S

dx = 1;

M

I x

Ф|

-M I

в

x i

S

x —

m xi

dx < м ,

S

1 lim— s^M

CS

, I x

Ф| -

в

\ xi

S

= 8( x - xi),

Cs > 0, Vs, s = 1, 2, 3, ...; Cs ^ 0, lim sC = m, s ^M где С - параметр размытости.

Оценка (2) должна удовлетворять условию воспроизводимости

x j = F j ( u ^j , x ^j , a ^j ), j = 1, q ^, x j = S j ( u ^j , x ^j , u s , x s ), j = q + 1, k , где F - параметрический оператор; 5 - непараметрический оператор; q - число параметрических уравнений; к - общее число уравнений.

По различным каналам связи многосвязной системы известна их параметрическая структура с точностью до параметров, для иных каналов связи такая информация отсутствует и их восстановление осуществляется средствами непараметрического оценивания. При этом предполагается однозначный характер зависимости входных-выходных переменных системы. В этом случае модель многосвязной системы представляет собой систему нелинейных стохастических уравнений, в которую входят как параметрические соотношения, так и непараметрические (3). Оценка выхода многосвязной системы осуществляется в результате решения взаимосвязанной системы указанных выше уравнений при известных значениях выходных переменных, модели которых обозначим Xi = F. ( u ' , v i , a ' ) , i = 1, k , где x ‘ , и, v . - соответственно выходная и входные переменные z-го объекта; F . - параметрическая зависимость X от и. с точностью до параметров a. ; а к - число объектов.

Численные исследования. При исследовании непараметрических комбинированных моделей (3) методом

статистического моделирования была взята система десяти нелинейных уравнений, описывающая объект, представленный на рис. 3. Размерности параметров были описаны выше. На измерения был наложен белый шум различного уровня. Расхождение, рассчитанное как нормированная среднеквадратическая ошибка, выходных значений модели (3), построенной по выборке наблюдений, с соответствующими выходными значениями объекта находилось в интервале 3...7% в зависимости от уровня наложенного шума и объема выборки.

Таким образом, ценка выхода многосвязной системы осуществляется в результате решения взаимосвязанной системы указанных выше уравнений при известных значениях выходных переменных. Рассматривается задача теории идентификации, состоящая в объединении интегрированной модели многосвязного процесса, объединяющей соответствующие фрагменты модели локальных объектов. В результате получен новый класс комбинированных моделей, объединяющий как параметрические, так и непараметрические модели различных каналов многосвязных систем.

Комбинированные модели были исследованы методом статистического моделирования. В качестве исход ного описания процесса были приняты по различным каналам связи полиномиальные зависимости. Моделирование осуществляется в обстановке случайных возмущений. При этом предполагалось, что структура по некоторым каналам использовалась при построении модели, а по некоторым каналам структура неизвестна. В системе, изображенной на рис. 3, присутствуют как статические, так и динамические объекты.

Для исследования комбинированной многосвязной системы была построена компьютерная модель. Для описания каждой связи были реализованы алгоритмы как параметрической, так и непараметрической теории идентификации и оптимизации.