О непараметрическом управлении линейной динамической системой

При управлении динамическими системами обычно предполагается известным уравнение объекта либо его передаточная функция с точностью до вектора параметров. В этом случае достаточно хорошо разра- ботаны методы анализа и синтеза систем автоматического регулирования и управления. В теории автоматического регулирования и управления, когда нет математического описания линейного динамического объекта, часто используются П-, ПИ- и ПИД-регуляторы. Настройка параметров последних является предметом анализа систем автоматического регулирования. В условиях непараметрической неопределенности, т. е. когда вид у уравнения, описывающего процесс, неизвестен, а известны лишь качественные характеристики, например, сведения о линейности процесса, классическая теория управления не может быть применена. Однако в рамках непараметрического подхода могут быть построены как модели исследуемого объекта, так и алгоритмы управления. В основе этого подхода лежат оценки переходных и весовых функций процесса. При этом этап выбора их с точностью до вектора параметров отсутствует. Для их восстановления используются соответствующие непараметрические оценки по результатам наблюдений переходных характеристик, «снятых» на исследуемом объекте.

Постановка задачи. Пусть динамический процесс относится к классу линейных. Кроме того, имеется возможность постановки эксперимента по «снятию» переходных характеристик объекта. Ясно, что эксперимент по «снятию» весовой функции системы провести, чаще всего, невозможно, из-за трудностей «подачи» на вход объекта дельта-функции. Заметим, что весовая функция объекта h ( t ) – производная переходной функции k ( t ), т. е. h ( t ) = k ' _t ( t ).

Известно, что для линейного динамического объекта выход объекта x(t) можно представить в виде оператора x(t) = A[u(t)], где u(t) - входное воздействие; А – линейный оператор [1]. Если для линейного оператора А существует обратный оператор A 1, то A 1A = I, где I - единичный оператор. В этом случае u(t) = A"*[x(t)]. Если x(t) = x *(t), где x *(t) - желаемая траектория x(t), то алгоритм управления примет вид u *( t) = A"'[ x *( t)], (1)

где u *( t ) – управление, которое приводит объект в состояние x *( t ) . Можно считать, что в этом случае u *( t ) – идеальное управление. В дальнейшем такой регулятор будем называть u -регулятором.

Непараметрический u -регулятор. Известно, что линейный оператор A можно описать следующим функционалом при нулевых начальных условиях (интеграл Дюамеля) [1]:

x ( t ) = A [ u ( t )] = J h ( t — t ) u ( t ) d т , (2) 0

где h ( t ) – весовая функция системы.

Известно, что оператор, обратный линейному оператору (2), имеет вид [2]:

u ( t ) = A ^-1 [ x ( t )] = J v ( t - t ) x ( t ) d т , (3) 0

где v ( t ) - весовая функция в направлении «выход-вход». Таким образом, если x ( t ) = x* ( t ), то u -регулятор будет иметь вид

u *( t ) = A 1 [ x *( t )] = J v ( t — t ) x *( t ) d т .       (4)

Однако ясно, что оператор А неизвестен, соответственно, не может быть найден и оператор A ^-1 . В данной ситуации целесообразно использовать в качестве модели (2) непараметрическую модель линейной динамической системы [2]:

t xn (t) = J hN (t -t, xN, tN) u (t) d т,           (5)

где h_N ( t — t , x_N , t_N ) - оценка весовой функции системы, а x_N = ( x 1 ,..., x_N ) и t _N = ( t 1 ,..., tN ) - временные векторы.

Переходную характеристику в направлении «выход–вход» будем «снимать» на модели (5). По видимому, впервые эта идея была высказана в [3], т. е. xN (t) = 1(t). В итоге, получим выборки un = (u1,..., un) и Fn = (t1,..., tn) - временные векторы. Для удобства дальнейшего изложения введем обозначение un = Бn = (to1,..., ton), подчеркивая тем самым, что ton - значение управляющего воздействия при условии, что xN (t) = 1(t). Тогда, оценка u-регулятора примет вид t u„(t) = Jv„(t-t)x*(t)dт .              (6)

В качестве оценок весовых функций h_N ( t ) и v _N ( t ) в дальнейшем используются непараметрические статистики.

Непараметрические оценки u -регулятора. Пусть после эксперимента имеем выборку наблюдений { xi = ki , ti }, i = 1, N , где N - объем выборки; ki - наблюдаемое значение выходной переменной объекта x ( t ) при u ( t ) = 1( t ) в момент времени t_i .

Для оценки переходной функции по выборке наблюдений воспользуемся непараметрической оценкой вида

NIN kN (t)=Z k^( tc^ )/£ф( CNr),(7)

i=1

где k_N ( t ) – оценка переходной функции в момент времени t по выборке объемом N ; Ф ( ■ ) - колоколообразная функция и параметр размытости C_N удовлетворяют некоторым условиям сходимости [4].

В качестве оценки весовой функции может быть использована разностная оценка весовой функции:

nIn hn (t) = ^ h>( CN )/Еф( CN),(8)

i=1

-   k?( t +A t) - k;( tj) . -— где h = —i---------—, i = 1, N, и непараметриче-

‘            At ская оценка весовой функции:

-               /,.х^ "

hN ( t ) = kN '( t ) = l £ X ^ ' ( ^ ) | £^ф ( ^ ) -

_V1=0

N,

• -I У х ф( м) 1Уф '( t i t") ЛУф( У") I.

I                 CN I              CN           I

V i=0             7 i=0           J/ V i=o

Для выражения (9) критерий оптимальности выбора параметра размытости принимает следующий вид:

" I      t- -

W ( C n ) = N 2 k, - f h ( ti, C n )

i=1 V      0

^ min . C N

Оценив весовую функцию объекта, мы построили оценку оператора, т. е. модель объекта в виде (5). Используя построенную модель, найдем обратную переходную функцию объекта. Для этого запишем модель вида (5) в дискретном виде:

ii

x [ i ] = 2 h [ i - j ] u [ j J A t ,             (11)

j =0

где x [ i ], h [ i ] , u [ i ] – значения функций x ( t ) , h ( t ) , u ( t ) в момент времени t_i . Фиксируя на выходе функцию Хэвисайда ( x [ i J = 1[ i J), найдем реализацию u [ i J = to i J:

i                                         i -i

1[ i J = 2 h [ i — j J tf j J A t = 2 h [ i - j J to j J A t + h [0J to t J A t , (12) j =0                         j =0

to [0J = 1/ h [0J A t ,

to [ i J =

i -1

1 -2 h [ i - j J®[ j JAt j=0

Вычислительные соотношения (13) дают выборку переходной характеристики объекта в направлении «выход–вход». Непараметрическая оценка переходной функции в направлении «выход-вход» или «обратной» переходной функции имеет вид:

nn

Й n ( t ) = 2 - Ф ( C t )/2ф( C T) .       (14)

i =1                           i =1

Производная от этой функции есть весовая функция в направлении «выход–вход», или «обратная» весовая функция. Оценка производной «обратной» переходной функции через конечные разности имеет вид nn v n (t) = 2-ф( ^ )/2ф( ^),   (15)

i =1                     / i =1

• -     to ( t, + A t ) - to ( t, ) . -—

где v, = ——--------—, i = 1, n .

i            A t

Непараметрическая оценка «обратной» весовой функции v ( t ) имеет вид nn

I E " , ^ф ' ( % ) ] Е^ф ( tC; ) -

V i=1

nn

-| E " ii ^ф( % ) 1 Е^ф ' ( ^)

vn (t) = ton'(t) = ^2=Lx-------^XX-------.(16)

n

| 2^ф ( tCT ) I

V i =1

Непараметрическая оценка (6) ( u_n -регулятор) будет иметь вид

k u ( tk ) =Ev N ( tk - tj) x *( tj )A t .

j =0

Численные исследования. В качестве объекта исследования рассмотрим динамический объект, поведение которого описывается дифференциальным уравнением первого порядка:

dx ( t )

a, ------+ a_ox ( t ) = a u ( t ),             (18)

1 dt 0

где a 1 = 1, a ₀ = 1, a = 1.

Переходная функция системы - k ( t ) = 1 - e ^- t , а весовая функция имеет вид h ( t ) = k '( t ) = e~t . «Обратная» переходная функция - w ( t ) = 8 ( t ) + 1( t ). Ее дискретный аналог с шагом дискретизации Δ t = 0,05 представлен на рис. 1. Обратная весовая функция – v ( t ) = w '( t ) = 8 '( t ) + 8 ( t ), дискретный аналог которой с шагом дискретизации Δ t = 0,05 представлен на рис. 2.

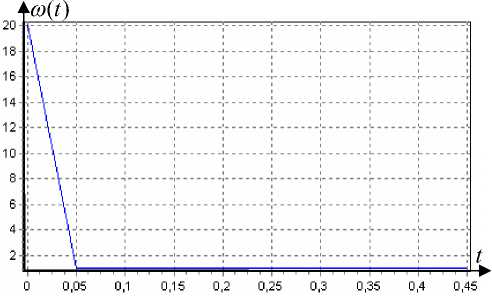
Рис. 1. w ( t ) в дискретном виде, первые 10 тактов

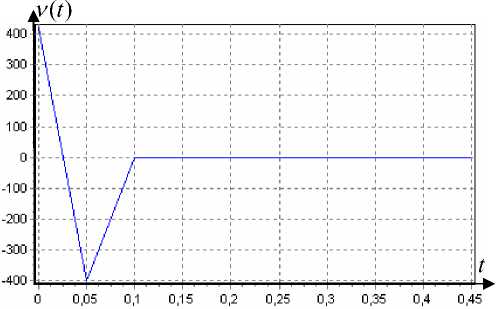
Рис. 2. ν ( t ) в дискретном виде, первые 10 тактов

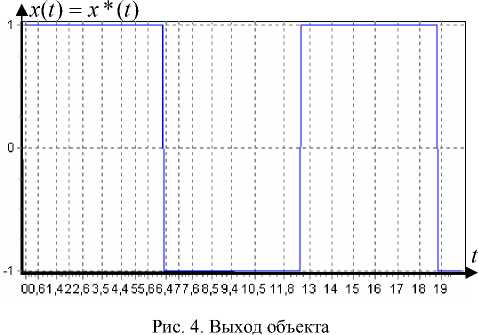
Управление для задания x* ( t ) = sign(sin( t/ 4)) представлено на рис. 3, реакция объекта на это управление, совпадающая с заданием, представлено на рис. 4.

Управление для случайного задания (случайный сигнал в области [–1; 1]) и реакция объекта на это управление, совпадающая с заданием, представлены на рис. 5 и рис. 6, соответственно.

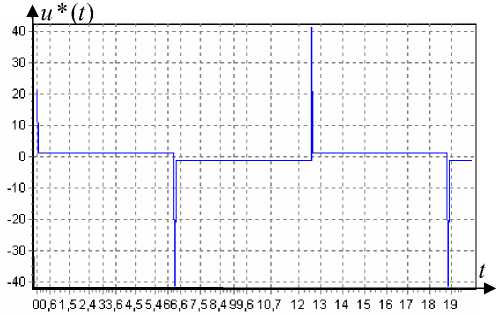
Рис. 3. Управление для задания x* ( t ) = sign(sin( t/ 4))

Теперь вернемся к исходной постановке задачи, где в качестве исходной информации используем выборку наблюдений входной и выходной величины. Решая численным методом (методом Рунге–Кутта) уравнение (18), сгенерируем выборку наблюдений, подав на вход функцию Хэвисайда.

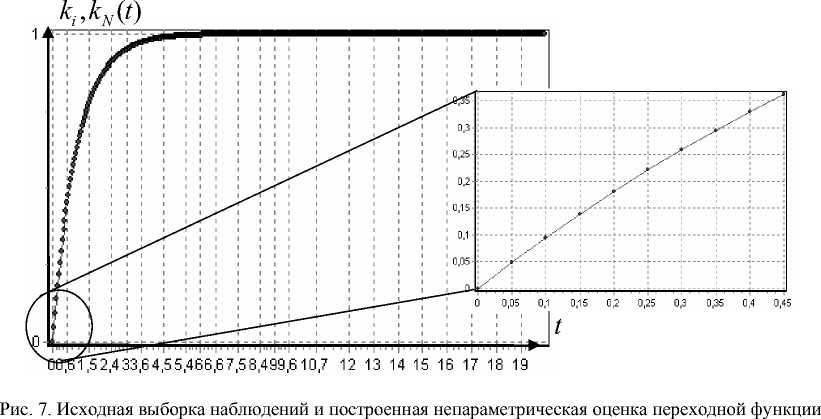
Получим выборку переходной характеристики объекта объемом N . В данном случае объем выборки составил N = 400 точек на временном интервале [0; 20], шаг дискретизации Δ t = 0,05. Для получения переходной функции по выборке используется непараметрическая оценка (7). Для решения «проблемы концов» при непараметрическом оценивании функции, исходная выборка дополняется десятью точками на концах интервала. Полученный результат представлен на рис. 7.

Рис. 6. Выход объекта

▲u *( t )

35---L

t

0 0,1 0,2 0,35 0,5 0,65 0,8 0,95 1,1 1,25 1,4 1,55 1,7 1,85 2 2,1 2,2 2,35

Рис. 5. Управление для случайного задания лx(t) = x*(t)

0 0,1 0,25 0,40,50,6 0,75 0,9 1 1,1 1,25 1,41,5 1,65 1,8 1,95 2,12,22,3 2,45

Рассмотрим два способа: оценивание через конечные разности и производную непараметрической оценки. В дальнейшем, будем приводить вычислительные результаты, полученные в случаях использования выражений (8) и (9), в сравнительной форме.

Оценки весовой функции для выражений (8) и (9) представлены на рис. 8. «Обратная» переходная функция представлена рис. 9.

.- h_N ( t ), h_N ( t ),

( t )

t

Рис. 11. Управление для задания x *( t ) = sin( t ).

Первые 200 тактов:

I – алгоритм через аналитические оценки производных; II – алгоритм через конечные разности

через (9)

через (8)

t

00,30,711 ,3 1 ,8 2,3 2,8 3,3 3,8 4,3 4,8 5,3 5,8 6,3 6,8 7,3 7,8 8,38,799,39,7

Рис. 8. Весовая функция системы. Первые 200 тактов

® n ( t ), О ^- n ( t )

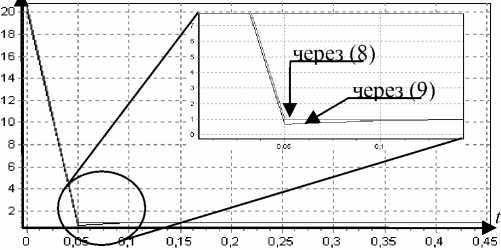
Рис. 9. Обратная переходная функция системы. Первые 10 тактов

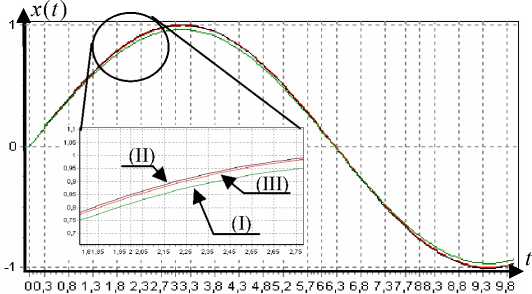
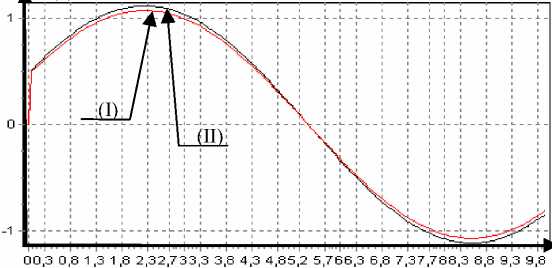
Рис. 12. Выход объекта и задание. Первые 200 тактов: I – алгоритм через аналитические оценки производных;

II – алгоритм через конечные разности; III – задание x *( t ) = sin( t )

Имея обратную переходную функцию системы, найдем обратную весовую функцию системы (рис. 10).

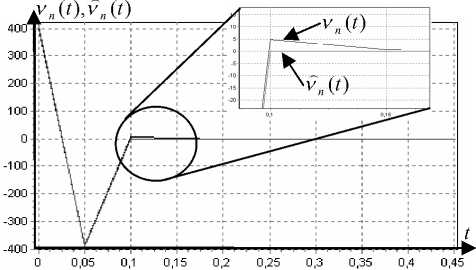
Рис. 10. Обратная весовая функция системы, первые 10 тактов

u ( t )

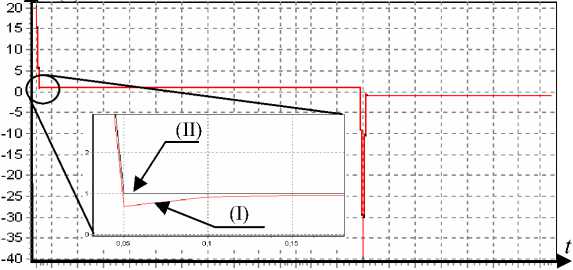
00,3 0,8 1 ,3 1 ,8 2,3 2,8 3,3 3,8 4,34,755,3 5,8 6,3 8,8 7,3 7,8 8,3 8,8 9,39,7

Рис. 13. Управление для задания x *( t ) = sign(sin( t /4)). Первые 200 тактов:

I – алгоритм через аналитические оценки производных; II – алгоритм через конечные разности

Получив оценку обратной весовой функции системы, мы построили оценку обратного оператора системы в виде (8). Оценка обратного оператора системы представляет собой регулятор системы. В качестве задания возьмем три траектории: x* ( t ) = sin( t ), x* ( t ) = sign(sin( t/ 4)), случайный сигнал в диапазоне [–1; 1]. Графические результаты рассчитанного управляющего сигнала и реакции объекта в сравнении с заданием приведены на рис. 11–16.

(II

(III)

t

00,3 0,8 1,3 1,8 2,32,733,3 3,8 4,3 4,85,2 5,766

,3 6,

8 7,

37,

788,

3 8,

8 9,

3 9,

Рис. 14. Выход объекта и задание. Первые 200 тактов: I – алгоритм через аналитические оценки производных;

II – алгоритм через конечные разности; III – задание x *( t ) = sign(sin( t /4))

ki , kN (t)

t

-30 ------------------------- 1-------------------------------------------^

0 0,05 0,1     0,2 0,25 0,3 0,35 0,45 0,5 0,55 0,65 0,7 0,75 0,8     0,9 0,95

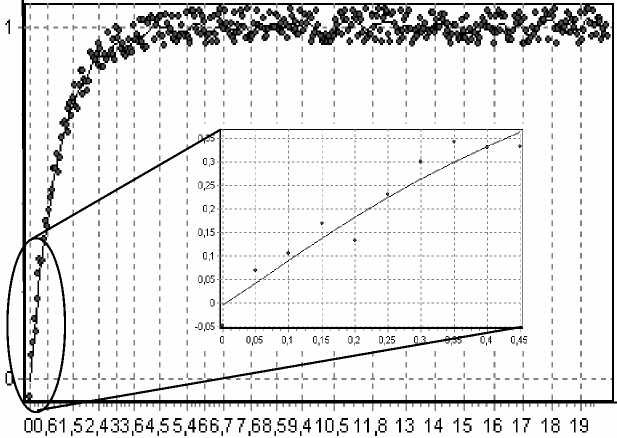
Рис. 17. Точки выборки и восстановленная переходная функция

t

-►

Рис. 15. Управление для случайного задания.

Первые 20 тактов

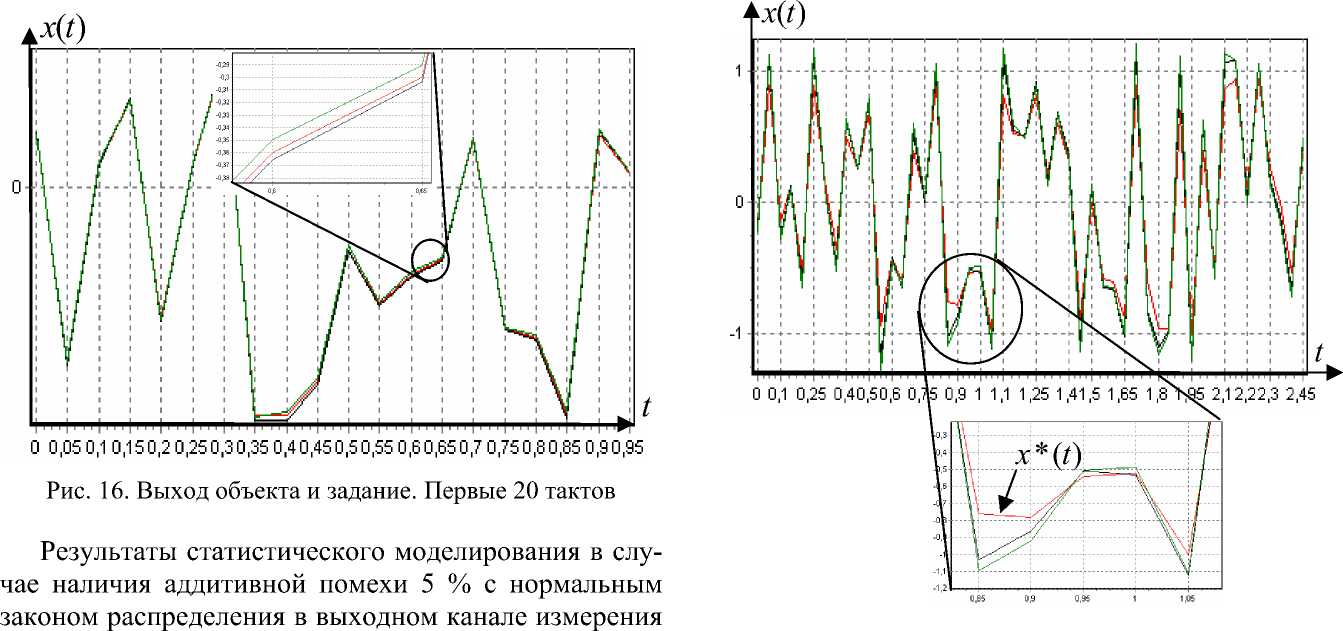
приведены на рис. 17–19.

Рис. 18. Выход объекта и задание. Первые 50 тактов

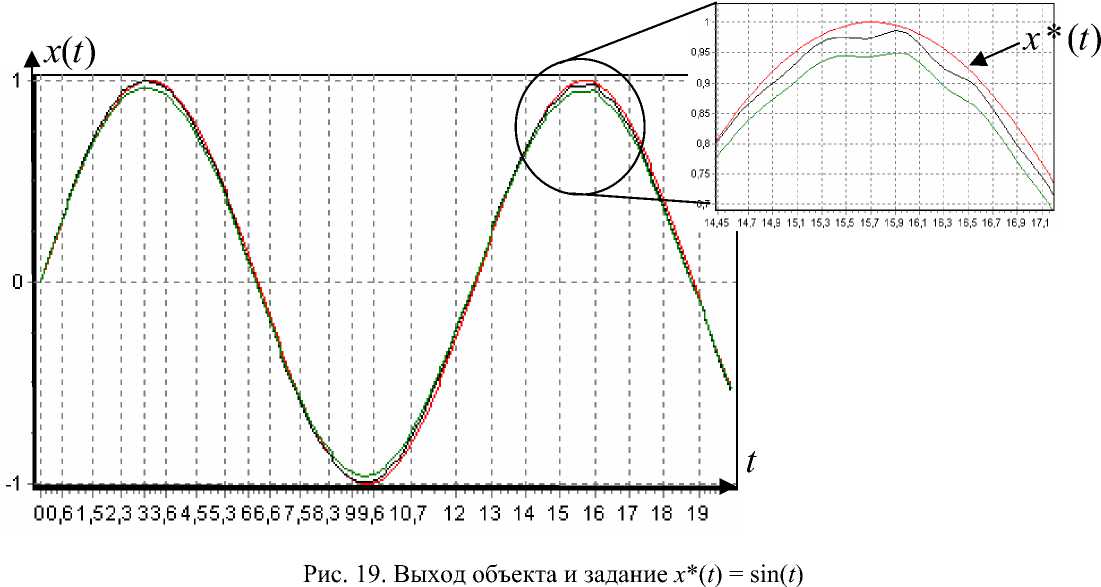
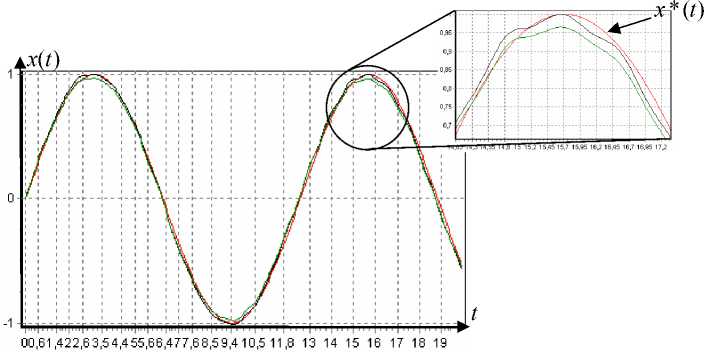
Рис. 20. Реакция объекта в сравнении с заданием x *( t ) = sin( t )

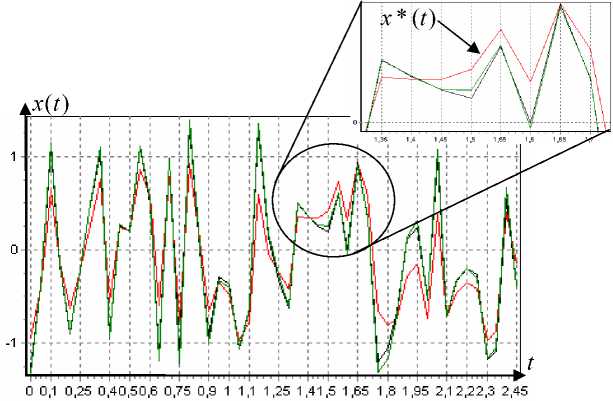
Рис. 21. Выход объекта и задание. Первые 50 тактов

Результаты статистического моделирования в случае наличия аддитивной помехи 10 % с нормальным законом распределения в выходном канале измерения приведены на рис. 20, 21.