О нижнем и верхнем вводе электронов в энергоанализатор типа цилиндрическое зеркало. Ч. 1

Энергоанализатор (ЭА) типа цилиндрическое зеркало (ЦЗ) широко применяется в различных научных исследованиях и технических приложениях (см. [1–3]).

Под нижним вводом подразумевается ввод электронов в дисперсное пространство через внутренний цилиндр (электрод) со стороны оси. Этот случай изучался в большом числе работ. Основы расчета ЦЗ с нижним вводом заложены в [4].

Верхний ввод, когда электроны вводятся в дисперсное пространство по направлению к оси через внешний цилиндр (электрод), изучался в работе [5]. Схема с верхним вводом в качестве самостоятельного энергоанализатора не нашла применения. Однако в совокупности с еще одним или двумя каскадами ЦЗ каскад с верхним вводом составил системы, которые уже нашли свое отражение в научной литературе. В [6] стыковка обычного ЦЗ (с нижним вводом) с ЦЗ с верхним вводом позволила спрямить линию фокусов, что важно для применения ЭА в режиме спектрографа. В [7, 8] ЦЗ с верхним вводом помещался между двумя обычными ЦЗ, т. е. была образована 3-каскадная система, в которой удалось получить фокусировку третьего порядка и даже фокусировку четвертого порядка. Вид ЦЗ показан на рис. 1.

Отметим, что в [5] исследовалась только фокусировка по углу первого порядка и только для схемы (внешние) цилиндр—цилиндр. Поэтому интересно провести исследование в ЦЗ с верхним вводом условий фокусировки второго порядка для схем, отличных от схемы (внешние) цилиндр– цилиндр.

Исследования в представленной работе проведены на идеальном ЦЗ со следующими параметрами:

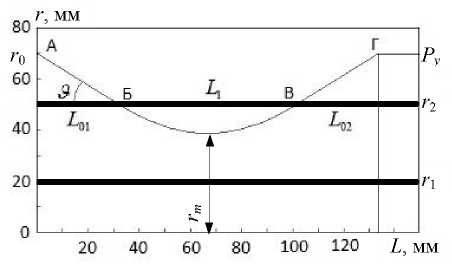
Рис. 1. Сечение ЦЗ плоскостью, проходящей через ось.

АБВГ — центральная траектория пучка электронов; A — источник электронов; Б — точка входа электронов в дисперсное пространство; В — точка выхода электронов из дисперсного пространства; Г — точка входа электронов в детектор; L — расстояние вдоль оси Z , отсчитываемое от источника электронов; r — радиус; r = 0 — ось ЦЗ; r = r ₁ — внутренний цилиндр (обкладка конденсатора); r = r 2 — внешний цилиндр; r 0 — радиус источника электронов; P y — радиус детектора электронов; L 01 — расстояние от источника до точки входа электронов в дисперсное пространство; L 02 — расстояние от точки выхода электронов из дисперсного пространства до детектора; L ₁ — расстояние, которое электроны пролетают в дисперсном пространстве; ϑ — угол наклона траектории к оси системы до входа электрона в дисперсное пространство; r m — наименьшее удаление траектории от оси в дисперсном пространстве.

Подробности в тексте радиус внутреннего цилиндра ЦЗ равен 20 мм; радиус внешнего цилиндра ЦЗ равен 50 мм;

на отражающем электроде выставлен потенциал U = - 100В, для нижнего ввода этот электрод — внешний цилиндр, а для верхнего ввода — внутренний; с боков осуществлено замыкание контура кольцами, на которых выставлено распределение потенциала, соответствующее идеальному цилиндрическому полю; электроны входят в дисперсное пространство и выходят из него через сетки, которые считаются идеальными, т. е. не вносящими никаких искажений в пучок электронов. Пучок электронов движется слева направо.

ВЫЧИСЛЕНИЕ ТРАЕКТОРИЙ ЭЛЕКТРОНОВ И ИХ ОБРАБОТКА

Как показано на рис. 1, электроны летят последовательно в бесполевом (А–Б), дисперсном (Б–В) и снова в бесполевом (В–Г) пространствах. Смещение электрона вдоль оси Z (проекция траектории на ось Z) равно L ₀₁ = ( r₀ - r 2 )/tg( 9 ) в первом бесполевом пространстве и L ₀₂ = ( P y - r ,)/tg( 9 ) во втором бесполевом пространстве. Суммарное (полное) смещение в двух бесполевых пространствах: L о = ( ( г 0 + P y ) - 2 r ) /tg( 9 ). Видно, что полное смещение электронов вдоль оси Z в бесполевом пространстве зависит от суммы P = P y + r ₀ — совокупного удаления источника и детектора от оси. Кроме того, можно ввести обозначение P 0 — совокупное удаление источника и детектора от электрода, через который электроны вводятся в дисперсное пространство. В случае верхнего ввода этот электрод — внешний цилиндр и P 0 = = ( r ₀ + P y ) - 2 r ₂; для нижнего ввода P 0 = = 2 r - ( r 0 + P ) .

В данной статье рассмотрим только те траектории, которые не имеют аксиальной компоненты скорости. Влияние аксиальной компоненты скорости на характеристики ЭА с верхним вводом рассмотрим во второй части данной работы, которая будет оформлена в виде отдельной статьи.

Для вычисления траекторий в дисперсном пространстве используем уравнения движения [9]:

z = 0, r = -Er m с граничными условиями z| = L01, z| = = vocos(9), r\t=0 = r2, rt=0 = vosin(9), где e, m — заряд и масса электрона, v0 — скорость электрона перед входом в дисперсное пространство, E r — радиальная компонента напряженности электрического поля.

Решение этой системы приведено в [5]. Мы далее будем применять обозначения, более близкие к [4], с некоторыми нашими изменениями.

Q sin( ϑ )

L ₂ = 4 r ₂ Qcos(&)e - Q 2 ^{sm2( 9} ) J e z 2 d z ,

где

r

Q=^eU 1 m I ^21 •

r ₁

T = mv 0

кинетическая

энергия электрона перед входом в дисперсное пространство, U ₁ — потенциал внутреннего цилиндра, потенциал внешнего цилиндра считаем равным нулю. В случае нижнего ввода в выражении для L ₂ следует Q заменить на B , отличающееся от Q тем, что в нем вместо U ₁ фигурирует U ₂ (здесь U 2 — потенциал на внешнем цилиндре).

x

Функция Dos( x ) = e - x ² J e z d z называется функци-

ей (интегралом) Досона [10] (о ее вычислении см. Приложение).

Вид зависимости полного смещения электрона вдоль оси Z при его пролете от источника до де-

тектора от угла старта при разных значениях энергии и фиксированном параметре P_y показан на рис. 2.

Видно, что кривые L(9) E _{= const}, вплоть до кривой с номером шесть, не содержат экстремумов. Т. е. ни одна из производных функции

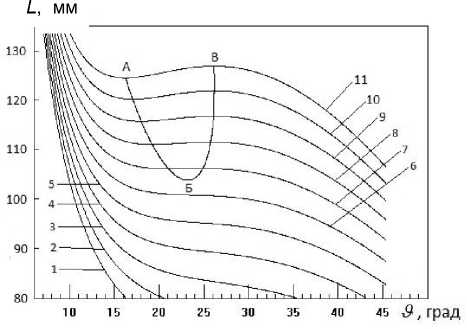
Рис. 2. Зависимость L ( 9 ) E _{= const} полного смещения электрона вдоль оси Z для верхнего ввода от угла старта при P y = 65 мм ( P 0 = 15мм) и различных энергиях электронов.

Цифры при каждой линии указывают на соответствующую энергию E (эВ): 1 — Е = 60, 2 — 70, 3 — 80, 4 — 90, 5 — 100, 6 — 110, 7 — 120, 8 — 130, 9 — 140, 10 — 150, 11 — 160.

Подробности в тексте

L(9)E=const по 9 не равна нулю, что свидетельствует об отсутствии фокусировки при этих энергиях. Начиная с седьмой кривой на них появляются экстремумы (минимум и максимум, в которых первая производная L(9}E=const по 9 равна нулю), т. е. появляются две фокусировки первого порядка. Соединив последовательные точки экстремумов (минимум с минимумом и максимум с максимумом), получим две ветви линии AБВ, которая похожа на деформированную параболу и которая представляет собой зависимость расстояния вдоль оси Z положения одного из экстремумов функции L(ϑ) от угла ϑ. При построении кривой АБВ использовались 1000 значений энергии. Каждый из этих экстремумов (точка на параболе) соответствует фокусу первого порядка, причем на линии AБ расположены минимумы функции L(ϑ) , а на линии БВ — максимумы. Вершина этой деформированной "параболы", в которой сливаются две ветви линии AБВ (два фокуса первого порядка), соответствует фокусу второго порядка. В результате мы для каждого заданного нами значения параметра P0 вычисляем значения E , L , ϑ, при которых осуществляется фокусировка второго порядка. Ниже будем обозначать эти параметры, определяющие положение фокуса второго поряд- ка, P2f, E2f, ϑ2f, L

2 f .

Такие кривые АБВ строим для множества значений параметра P 0 : для нижнего ввода P 0 = 0– 40 мм и для верхнего ввода P ₀ = 0–20 мм. На рис. 3

показаны кривые положения фокусов первого порядка, построенные для нижнего ввода (рис. 3, а) и верхнего ввода (рис. 3, б).

На рис. 3 видно, что только линия с номером 1 (ей соответствует величина параметра P 0 = 0 мм, когда источник и приемник расположены на поверхности цилиндра, через который производится ввод электронов в дисперсное пространство) отличается от остальных своим видом. В диапазоне входных углов 9 = 6 ^ 50 ° эта линия имеет только правую часть, т. е. соответствующая линия L ( 9 ) E = _const имеет только максимум, что указывает на наличие только одного фокуса первого порядка. Второго фокуса первого порядка и фокуса второго порядка на этой кривой не наблюдается. Для схемы (внутренние) цилиндр—цилиндр на отсутствие фокусировки второго порядка указано в работах [11, 12]. Схема (внешние) цилиндр—цилиндр рассмотрена только в работе [5], и в ней рассмотрена только фокусировка первого порядка.

Таким образом, для нижнего и верхнего вводов электронов в ЦЗ вблизи электрода, через который электроны попадают в дисперсное пространство (малая величина P ₀ ), существует граница, которая отделяет пространство, в котором возможна фокусировка второго порядка от пространства, в котором она уже невозможна.

В схеме с нижним вводом (рис. 3, а) в случае больших P ₀ (при удалении от нижнего электрода в сторону оси) линия № 21 ( P 0 = 40 мм) соответствует

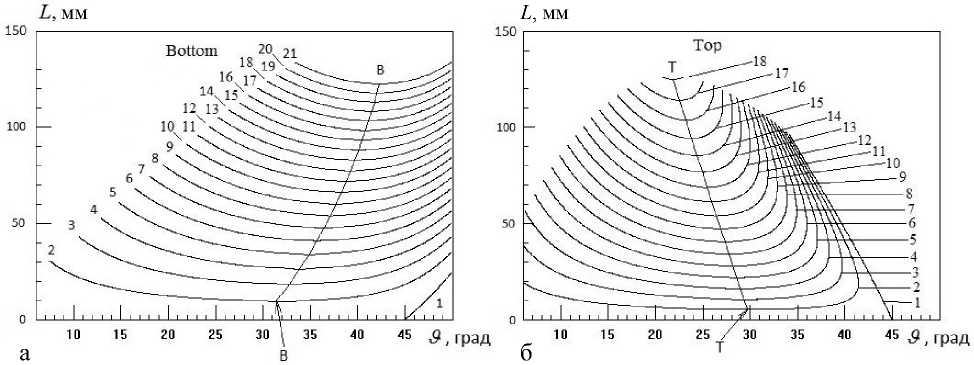
Рис. 3. Графики зависимости L ext (д')_P =_const ( L ^extr = Z -координата экстремумов зависимости L(9) E = _const от угла ϑ ) при разных значениях P ₀ .

Слева (а) показана зависимость положения фокусов первого порядка от угла старта электронов для случая нижнего ввода электронов в дисперсное пространство, а справа (б) — для случая верхнего ввода электронов. Цифры на (а), стоящие рядом с каждой линией, соответствуют величине параметра P ₀ (мм): 1 — P ₀= 0, 2 — 2, 3 — 4, 4 — 6, 5 — 8, 6 — 10, 7 — 12, 8 — 14, 9 — 16, 10 — 18, 11 — 20, 12 — 22, 13 — 24, 14 — 26, 15 — 28, 16 — 30, 17 — 32, 18 — 34, 19 — 36, 20 — 38, 21 — 40. Цифры на (б), соответствуют величине параметра P ₀ (мм): 1 — P ₀ = 0, 2 — 1, …, 18 — 17.

Подробности в тексте

случаю, когда и источник, и детектор лежат на оси. При рассмотрении значений P 0 , при которых и источник, и детектор лежат дальше в области "за осью", найдено, что по крайней мере до P 0 = 80 мм фокусировка второго порядка существует. Это соответствует случаю, когда и источник, и приемник лежат на противоположной стороне внутреннего цилиндра. Случаи, когда детектор располагается за осью, рассмотрены в работе [13] (см. [13, рис. 3. I–III]).

В схеме с верхним вводом (рис. 3, б) последней является линия с № 18 (с P 0 = 17 мм). А следующая линия № 19 уже отсутствует, т. к. уже отсутствуют как фокусировка второго порядка, так и фокусировка первого порядка. Как оказалось, это связано с недостаточно большим диапазоном, рассматриваемых энергий. При увеличении этого диапазона значения параметра P 0 , при которых еще возможна фокусировка второго порядка, увеличиваются.

Подробнее границы (нижнюю и верхнюю) для нижнего и верхнего вводов рассмотрим во второй части данной работы.

Интересным является то, что на рис. 3, б, когда источник и детектор расположены вблизи внешнего цилиндра, линия экстремумов идет почти параллельно оси углов ϑ . Это говорит о том, что электроны, испущенные в широком диапазоне углов, практически сходятся в одну точку. Поэтому вполне возможно получить высокое пропускание 25–40 град.

Как было сказано выше, там, где стыкуются правая и левая линии фокусов первого порядка, находится фокус второго порядка. Соединим на рис. 3, а (и на рис. 3, б) точки ( E,ϑ), которые соответствуют фокусам второго порядка, и получим соответственно линию В–B и линию T–T. В [4] линия Py (L) называлась линией фокусов. В нашем случае каждую из линий В–B или T–T можно было бы назвать линией фокусов второго порядка. Разница в том, что в [4] линия фокусов определялась в пространстве (R, Z), в данной работе на рис. 3 — в пространстве ( L,ϑ).

В результате нахождения фокуса второго порядка (см. рис. 2 и рис. 3) вычисляются 4 параметра P _{2 f} , L _{2 f} , E _{2 f} , ϑ _{2 f} , определяющие положение фокуса второго порядка в пространстве ( P ₀, L , E , ϑ ) (точнее говоря, P ₀ = P _{2 f} мы задаем). Между этими параметрами наблюдается взаимно-однозначное соответствие. Любой из этих параметров может быть выбран в качестве "базового", по отношению к которому можно строить зависимости остальных параметров. Если построить зависимость P _{2 f} , E _{2 f} , ϑ _{2 f} от L _{2 f} , то получим некоторые линии для нижнего ввода и верхнего ввода в ЦЗ, в каждой точке которых существует фокусировка второго порядка. Эти линии показаны на рис. 4. Эти линии вместе впервые приведены в [14]. Совокупность этих линий можно назвать обобщенной линией фокусов второго порядка, т. к. именно совокупность этих линий полностью задает параметры фокусов второго порядка.

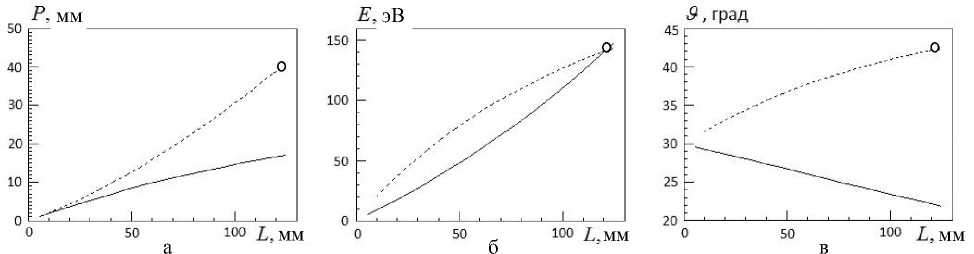
Рис. 4. Обобщенная линия фокусов показана в зависимости от положения выходной диафрагмы вдоль оси Z для ЦЗ для случаев нижнего (точечные линии) и верхнего (сплошные линии) ввода электронов в дисперсное пространство.

На (а) показаны зависимости суммарного удаления (источника и детектора) от цилиндра, через который производится ввод электронов в дисперсное пространство; на (б) показаны зависимости энергии, при которой реализуется фокусировка второго порядка; на (в) показаны зависимости угла старта центральной траектории для фокусировки второго порядка. Полый кружок на каждом из рисунков представляет собой результат, полученный в [4] для фокусировки второго порядка. Подробности в тексте

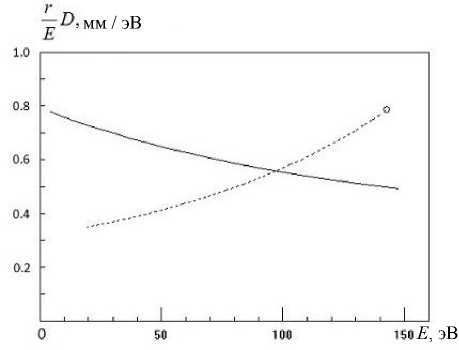
Рис. 5. Графики зависимости коэффициента

и размещение и источника, и детектора в непосредственной близости от этого цилиндра возможны только при исследовании спектров электронов малых и сверхмалых энергий. Кроме того, L ^ 0 означает, что и максимальное удаление электронов r max от этого цилиндра тоже будет стремиться к нулю. В результате две эти величины ( L и r _max) могут стать сравнимыми с размером ячейки сетки, через которую производится ввод электронов в дисперсное пространство. Это может привести к резкому увеличению влияния неоднородностей электрического поля, вносимых ячейками сетки, на пучок (его расфокусировку), что является крайне нежелательным.

(^rD/ La l/

( Ee)  A EE

для нижнего ( r = r 1

точечная ли-

ния) и верхнего ( r = r ₂, сплошная линия) вводов от энергии фокусировки при выполнении условия фокусировки второго порядка.

Кружочек, лежащий на графике для нижнего ввода, показывает результат, полученный в [4] для

схемы ось—ось.

Подробности в тексте

СРАВНЕНИЕ ХАРАКТЕРИСТИК НИЖНЕГО И ВЕРХНЕГО ВВОДОВ

Смещение A L точки прихода траектории на детектор при изменении энергии на величину A E

определяется выражением [1] A L =

(rDE)

A E , где

D — дисперсия по энергии. Нам интересен коэффи-

циент

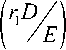
, который определяет это смещение.

Если сравнивать линии P ₀ ( L ) для нижнего и верхнего ввода (см. рис. 4, а), то видно, что линия для нижнего ввода имеет примерно в 2 раза больший угол наклона к оси L , чем линия для верхнего ввода. Поэтому верхний ввод несколько удобнее для использования ЦЗ в качестве спектрографа или многодетекторного спектрометра.

На рис. 4, б, линия E _{2 f} ( L ) для верхнего ввода лежит ниже этой же линии для нижнего ввода. Следовательно, при расположении детектора на одном расстоянии L для верхнего ввода и нижнего ввода энергия фокусировки второго порядка для верхнего ввода будет меньше. С другой стороны, если выбрать некоторую энергию E , одинаковую для верхнего и нижнего вводов, то в случае верхнего ввода длина L _{2 f} будет заметно больше. Это связано с тем, что угол старта центральной траектории пучка электронов для верхнего ввода заметно меньше, чем для нижнего ввода.

Вернемся к обсуждению возможности фокусировки второго порядка для схемы цилиндр—цилиндр (внешний или внутренний). Из рис. 4, а, видно, что при P 0 ^ 0 (т. е. вблизи этого цилиндра) и L ^ 0. А из рис. 4, б, видно, что в этом случае E ^ 0. Поэтому фокусировка второго порядка

Для нижнего ввода выражение для этого коэффициента приведено в [4] при выполнении условия фокусировки второго порядка. В обозначениях данной работы это выражение имеет вид r         2r

— ^D bottom = — ^B cos ^{S x}

EE

х[2B sin S + (1 + 2B2 sin2 S)^eB2™2 Serf(B sin S)], где erf — интеграл вероятностей в версии справочника [10].

Подобное выражение можно получить для аналогичного коэффициента для схемы с верхним вводом r       2r

• —D = —² Q cos Sx

_E top _E

• x[ Q sin S + (1 - 2 Q ² sin ² S )Dos( Q sin S ) ] .

Графики зависимости этих коэффициентов от энергии электронов приведены на рис. 5.

Из рис. 5 видно, что обсуждаемый коэффициент, пропорциональный дисперсии по энергии, и для нижнего ввода, и для верхнего ввода имеет примерно один порядок. Различие не более чем в 2 раза. Для нижнего ввода этот коэффициент растет с ростом энергии, а для верхнего ввода — падает.

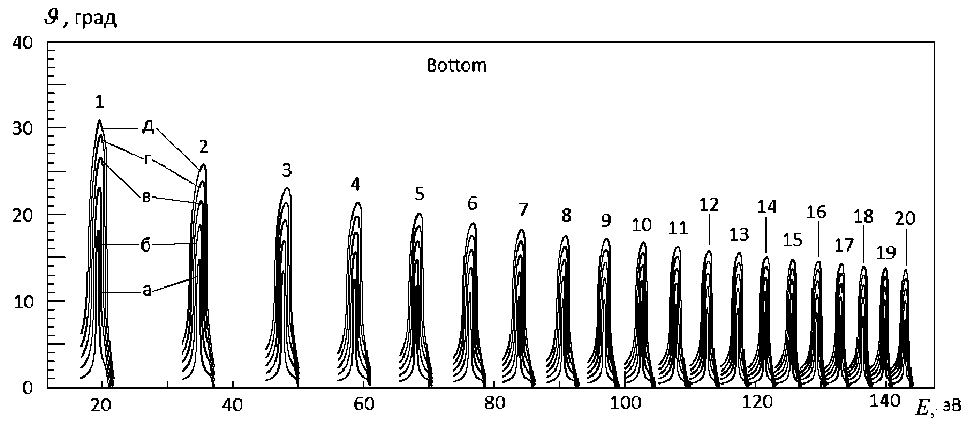
Рис. 6. Вид аппаратной функции для ЦЗ с нижним вводом вдоль линии фокусов второго порядка при разных значениях размера ВД.

Цифры над каждым семейством пиков соответствуют номерам на рис. 3, а. Буквы указывают на размер зазора ВД h (мм): а — h = 0.2, б — 0.4, в — 0.6, г — 0.8, д — 1.0.

Подробности в тексте

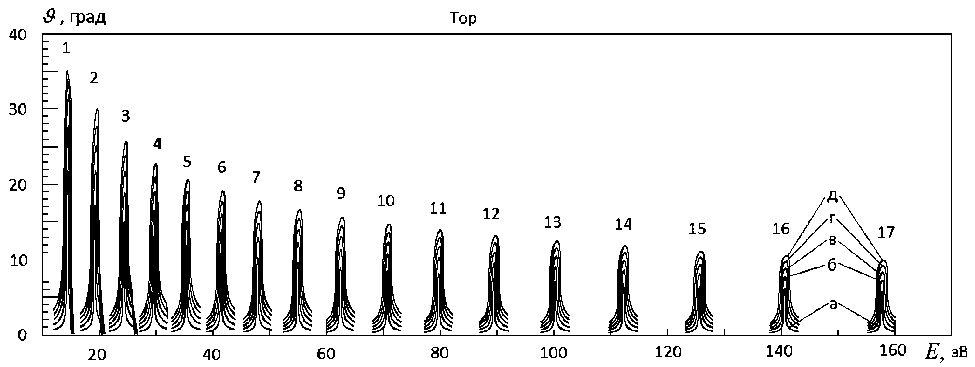
Рис. 7. Вид аппаратной функции (диапазона углов старта, с которыми траектории проходят в ВД) для ЦЗ с верхним вводом вдоль линии фокусов второго порядка при разных значениях размера ВД.

Цифры над каждым семейством пиков соответствуют номерам на рис. 3, б. Буквы указывают на размер зазора ВД h (мм): а — h = 0.2, б — 0.4, в — 0.6, г — 0.8, д — 1.0.

Подробности в тексте

Причем при энергии, приблизительно равной энергии, которую электрон приобретает, пройдя разность потенциалов U , эти коэффициенты сравниваются. При энергии, большей e ⋅ U , коэффициент для нижнего ввода становится больше, чем коэффициент для верхнего ввода.

Одним из интереснейших и важнейших свойств ЭА является вид его аппаратной функции (АФ). В качестве АФ будем использовать диапазон углов старта, с которыми траектории проходят в зазор выходной диафрагмы (ВД). Для построения графиков АФ будем пользоваться методом, который кратко описан в [15] и назван там проверочным и более подробно рассмотрен в [16]. На рис. 6 и рис. 7 приведены АФ для схем ЭА с нижним и верхним вводами для параметров, для которых выполняется фокусировка второго порядка, т. е. вдоль линии фокусов второго порядка. Видно, что по мере уменьшения P2 f (что означает приближение от оси к внутреннему цилиндру) величина пиков растет (растет пропускание). Однако и ширина пиков растет.

В отличие от нижнего ввода при верхнем вводе (см. рис. 7) при приближении к верхнему цилиндру (электроду) с внешней стороны пики АФ становятся выше и у же. То есть заметно растет пропускание и уменьшается абсолютная величина разрешения.

При приближении к электроду, через который производится ввод электронов в дисперсное пространство, для схемы с нижним вводом расстояние между соседними пиками увеличивается, а для верхнего ввода это расстояние уменьшается. С другой стороны, для нижнего ввода при удалении от этого электрода и при приближении к оси разница энергии между соседними пиками уменьшается, а в случае внешнего ввода при удалении от внешнего электрода — увеличивается.

Из графика (зависимости) АФ от энергии можно вычислить пропускание (угловой зазор, рис. 8) и разрешающую силу (рис. 9). Из рис. 8 видно, что зависимость пропускания ЦЗ от энергии электронов и для нижнего, и для верхнего вводов примерно одинакова. Это — падающие с ростом энергии фокусировки кривые. Пропускание для нижнего ввода выше в 1.5 ^ 2 раза.

Видно, что для нижнего и верхнего вводов разрешающая сила имеет один порядок и различается не более чем в 2 раза. Разрешающая сила при энергии электронов, большей e • U , больше для нижнего ввода, а при меньшей энергии наоборот.

ОБСУЖДЕНИЕ И ВЫВОДЫ

Схемы ЦЗ с нижним и верхним вводом электронов в дисперсное пространство оказываются близки по своим свойствам. При рассмотрении зависимостей L(&) E _{= const} (полного смещения электрона вдоль оси Z от угла старта ϑ ) видно, что для обоих типов ввода на ряде линий L(&) E _{= const} не наблюдается экстремумов, на ряде линий наблюдаются два экстремума (минимум и максимум) и существует одна линия, на которой расположена точка перегиба, в которой д ² L / д ^² = 0 , что говорит о нахождении в этой точке фокусировки не менее чем второго порядка.

Линии, соединяющие точки фокусов первого порядка (на графике L(&) P _{= const}), для нижнего ввода похожа на параболу, а для верхнего ввода эта линия также похожа на параболу, но с несколько сдвинутым вбок верхом. Эти параболы как для нижнего, так и для верхнего вводов, чем дальше от электрода, через который электроны

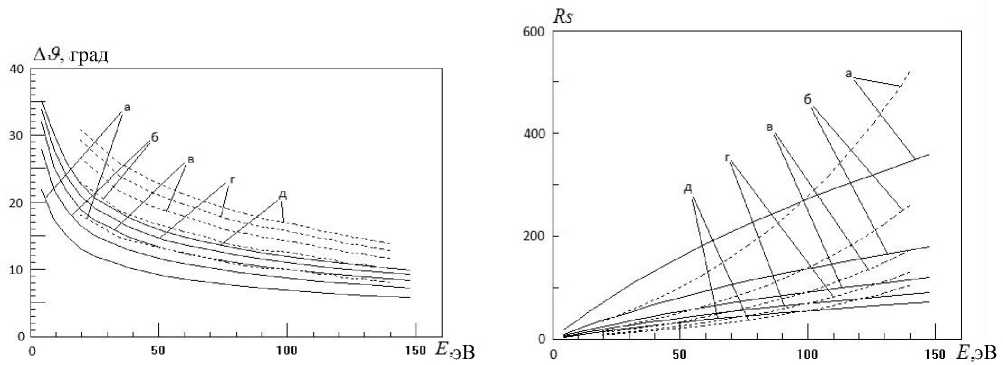
Рис. 8. Зависимость пропускания, выраженного в градусах (угловой зазор) для нижнего (точечная линия) и верхнего (сплошная линия) вводов от энергии электронов для различных величин выходной диафрагмы.

Буквы при каждой кривой указывают на размер зазора ВД h (мм): а — h = 0.2, б — 0.4, в — 0.6, г — 0.8, д — 1.0.

Подробности в тексте

Рис. 9. Разрешающая сила в зависимости от энергии электронов для нижнего (точечная линия) и верхнего (сплошная линия) вводов для различных величин выходной диафрагмы.

Буквы при каждой кривой указывают на размер зазора ВД h (мм): а — h = 0.2, б — 0.4, в — 0.6, г — 0.8, д — 1.0.

Подробности в тексте

вводятся в дисперсное пространство, тем они в области, в которой стыкуются правая и левая части этих кривых, ближе к идеальным параболам (симметричнее). Однако даже в этом случае "параболы" для верхнего ввода остаются несколько скошенными.

Из вида совокупности этих парабол можно сделать вывод, что для схемы цилиндр—цилиндр (внешний или внутренний) фокусировка второго порядка не наблюдается. То есть вблизи этого цилиндра находится некая граница области, в которой возможна фокусировка второго порядка. При удалении от этого цилиндра (в сторону к оси и за нее — в случае нижнего ввода, или от оси — в случае верхнего ввода) не наблюдается исчезновения фокусировки второго порядка и фокусировки первого порядка. То есть с этой стороны при предварительном рассмотрении пока не обнаружена граница , за которой фокусировка второго порядка и фокусировка первого порядка невозможны.

Дисперсия по энергии для верхнего ввода имеет такой же порядок, как и дисперсия для нижнего ввода. Но характер изменения с изменением энергии другой. Если для нижнего ввода дисперсия по энергии растет с ростом энергии, то для верхнего ввода она падает. При энергии, приблизительно равной e • U , эти две дисперсии сравниваются.

Аппаратная функция (АФ) для нижнего ввода становится шире при приближении к электроду, через который электроны вводятся в дисперсное пространство, а для верхнего ввода она становится у же.

По высоте пики АФ для обеих схем ввода растут при приближении к этому электроду. То есть пропускание увеличивается (см. рис. 6–8).

Разрешающая сила при приближении к электроду в обоих случаях уменьшается.

Таким образом, при рассмотрении только электронов, не имеющих аксиальной составляющей скорости, можно сделать вывод, что характеристики верхнего ввода электронов в спектрометр при имеющихся отличиях весьма близки к характеристикам нижнего ввода.

ПРИЛОЖЕНИЕ.

ВЫЧИСЛЕНИЕ ФУНКЦИИ (ИНТЕГРАЛА) ДОСОНА

Проводим с интегралом Досона преобразования

• 2 Г xa

Dos( x ) = e x J + J e x d x =

• V 0

= e - x 2 I e x ² D^os( x a ) + ⁽ x ^- x a ) £ A gn ) x n I .

V                             n = 1

квадратурную формулу Гаусса для десяти узлов, где x n = x a + x gn ) ( x - x a ); x gn ) и A gn ) — абсцисса и весовой коэффициент с номером n , значения которых брались нами из [10].

С помощью этой формулы интеграл Досона для больших значений x приводится к виду, содержащему сумму значений интеграла Досона в некоторой промежуточной точке x_a и квадратуры Гаусса от интеграла на отрезке, который мы стараемся сделать малым. Таблицы значений интеграла Досона приведены в [10].

В данной работе использовалась совокупность формул x = (0 ^ 1.0):

Dos( x ) = Gauss (0, x );

x = (1.0 ^ 2.0):

Dos( x ) = 0.5380795069 • e ¹ + Gauss (1.0, x );

x >  2.0:

Dos( x ) = 0.3013403889 • e ⁴ + Gauss (2.0, x ).

При таком представлении ошибка в пределах используемого в данной работе диапазона изменения x составляет не более нескольких единиц в десятом знаке.