О нормировании показателей уровня жизни населения

Единая методика оценки уровня жизни населения до настоящего времени отсутствует, однако общепринятой является точка зрения, что национальное развитие следует оценивать не только по национальному доходу, но также по ожидаемой продолжительности жизни и уровню грамотности. Этот принцип заложен в основу разработанного Программой развития Организации Объединенных Наций в 1990 г. индекса развития человеческого потенциала, включающего компоненты, отражающие достижения по каждому из трех измерений – дохода, долголетия и образования [1].

Принятый на страновом уровне подход к оценке качества и уровня жизни, в главных чертах, сохраняется и на региональном уровне [2]. Однако дискуссионными являются вопросы методологии и методов разработки системы показателей, в своей совокупности позволяющих давать более ли менее адекватные оценки уровня жизни населения регионов. Такая система должна не только достаточно полно характеризовать важнейшие компоненты качества жизни, но и позволять проводить анализ и синтез частных показателей как непременное условие их интегрирования в обобщающий региональный индикатор.

Из перечня задач, сформулированных С.А. Айвазяном в [2], наиболее дискуссионными, по нашему мнению, являются:

• 1)    определение исходного (априорного) перечня частных критериев синтетической категории качества жизни, влияющих на формирование значений интегрального индикатора этой категории;

• 2)    отбор из априорного перечня частных критериев анализируемого свойства качества жизни относительно небольшого числа частных критериев, играющих решающую роль в формировании значений соответствующего интегрального показателя;

• 3)    переход к унифицированным шкалам в измерении частных и интегральных критериев анализируемого свойства качества жизни.

С учетом накопленного нами опыта в области региональной экономики [3], статистических и социологических исследований качества жизни населения Центральной России [4], а также результатов теоретических исследований в области качества жизни населения других авторов [5-12], нами сформулированы следующие положения методологического подхода к построению частных и обобщенных индексов уровня жизни населения различных территориальных образований [13]:

• (1)    индекс должен быть безразмерной величиной, которая варьирует в открытом интервале от 0 до 1, асимптотически приближаясь к нулю в случае абсолютно неприемлемых значений образующих его показателей и к единице в случае очень хороших их значений;

• (2)    форма объединения частных индексов в обобщенный индекс должна устанавливаться, исходя из степени их взаимосвязи: при сильной корреляции частных индексов целесообразно использовать аддитивную форму объединения, при слабой их коррелированности – мультипликативную;

• (3)    веса (приоритеты) частных индексов должны быть установлены либо экспертным путем, либо, что предпочтительнее, с учетом статистических характеристик реальных выборок региональных данных.

Взамен естественного нормирования, в качестве нормирующего преобразования нами предлагается использовать психофизическую шкалу Харрингтона [14], которая ставит в соответствие значения формируемой на ее основе функции желательности лингвистической переменной с уровнями «очень плохо», «плохо», «удовлетворительно», «хорошо», «очень хорошо». В случае монотонности функции желательности, имеющей место практически для всех показателей качества жизни населения, шкала Харрингтона выглядит следующим образом – таблица 1.

Таблица 1. Числовые интервалы шкалы Харрингтона для монотонной функции желательности

Лингвистическая оценка (уровни лингвистической переменной)	Интервалы значений функции желательности d ( x )
Очень плохо	0,00-0,20
Плохо	0,20-0,37
Удовлетворительно	0,37-0,63
Хорошо	0,63-0,80
Очень хорошо	0,80-1,00

Практически достаточно ограничиться тремя градациями шкалы Харрингтона, отвечающим уровням (оценкам) «плохо», «удовлетворительно», «хорошо» [15]. В этом случае зона, соответствующая уровню «удовлетворительно», расширяется от 0,37 до 0,69, а зоны «плохо» и «хорошо» характеризуются интервалами (0,00-0,37) и (0,69-1,00) соответственно.

Аналитически функция желательности Харрингтона задается следующими формулами:

d i = d (z i ) = exp (-exp (-z i ));                (1)

z i = (х i – х i0 )/( х i1 – х i0 ),                       (2)

где zi – кодированные значения i-го показателя, представляющие собой безразмерные величины;

х i – значение i-го информативного показателя;

• х i0    и х i1 – границы зоны «удовлетворительно» в исходной шкале:

d i0 = d (z i (х i0 )) = 0,37;  d i1 = d (z i (х i1 )) = 0,69. (3)

При кодированном значении информативного показателя z =0 (нижняя граница зоны «удовлетворительно») функция желательности принимает значение 0,368, а при z =1, что соответствует верхней границе зоны «удовлетворительно», d ( z )=0,692. Таким образом, для построения функции желательности Харрингтона достаточно установить границы исходных показателей х i 0 и х i 1 , внутри которых изучаемая характеристика может считаться удовлетворительной. В частности, часто эти значения полагают равными х i 1 = х max и х i 0 = х min , т.е. соответственно максимальному и минимальному значению показателя по массиву региональных данных.

Такой подход, однако, представляется не вполне обоснованным: при этом все рассматриваемые статистические объекты в выборке считаются «удовлетворительными», тогда как исходя из общих соображений, это не так – в любом случае есть «лидеры», есть и «аутсайдеры». В работе [16] предложен иной подход – нижнюю границу зоны «удовлетворительно» положить равной значению параметра центральной тенденции (медианы или средней арифметической величины), а ее верхнюю зону «сдвинуть» в сторону значений показателя, отстоящих от параметра центральной тенденции на величину стандартного отклонения. Согласно правилу «трех сигм», тогда примерно 1/6 часть статистических объектов будет характеризоваться оценкой «удовлетворительно», половина – оценкой «плохо», 1/3 – оценкой «хорошо».

Предлагаемый в [16] статистический подход к назначению параметров функции Харрингтона, однако, имеет следствием существенное завышение требований к уровню показателей качества жизни, что не всегда оправдано. Чаще встречаются случаи, когда основная часть статистических единиц находится в зоне «удовлетворительно», и требуется их упорядочить, а также установить немногих «лидеров» и «аутсайдеров». В этих случаях более подходящим является следующая модификация описанного выше «статистического» подхода к расчету параметров функции Харрингтона:  нижнюю границу зоны

«удовлетворительно», в случае нормального распределения показателя, целесообразно положить равной среднему арифметическому показателя за минусом его стандартного отклонения, а верхнюю зону, как и ранее, «сдвинуть» в сторону значения показателя, превышающего среднее арифметическое на стандартное отклонение. Тогда в зоне «удовлетворительно» будет примерно 2/3 статистических единиц, а в зонах «плохо» и «хорошо» – по 1/6 статистических единиц.

Рассмотрим этот алгоритм на примере индекса продолжительности обучения как составной части ИРЧП.

Согласно методике расчета ИРЧП, принятой в Докладе ООН о развитии человека 2010 года [17], в качестве одного из показателей уровня образования принята средняя продолжительность обучения. Так, в 2000 г. в США этот показатель составлял 13,2 лет. Отечественной статистикой средняя продолжительность обучения в региональном разрезе не регистрируется, однако значения показателя можно рассчитать по данным ежегодного справочного издания «Регионы России. Социально-экономические показатели», где приведен состав занятого населения по уровню образования – доли занятого населения, имеющего послевузовское образование, высшее, среднее и начальное профессиональное образование, среднее полное (общее) и основное общее образование, а также населения, не имеющего основного образования. Доли занятого населения, имеющего послевузовское образование, составляют несколько десятых долей процента, и в поздних изданиях справочника они не приводятся (см., например, [18]). Полагая, в среднем, длительность обучения лиц, имеющих высшее, среднее и начальное профессиональное образование 16, 14 и 13 лет соответственно, лиц, имеющих среднее полное (общее) и основное общее образование, 11 и 9 лет соответственно, можно рассчитать среднюю продолжительность обучения населения в том или ином регионе РФ.

Рисунок 1 демонстрирует ранжирование регионов ЦФО по данному показателю, по данным 2013 г. Как видно из рисунка 1 б , распределение данного показателя по однородной выборке регионов ЦФО (без Москвы) близко к симметричному, тест Колмогорова-Смирнова также не выявил статистически значимого отклонения от нормального закона, и это позволило принять нулевую гипотезу нормальности распределения средней продолжительности обучения занятого населения с параметрами: среднее арифметическое (невзвешенное) – 13,537 лет и стандартное отклонение – 0,196 лет. Отсюда получаем: нижняя граница зоны «удовлетворительно» х 0 =13,34 лет; верхняя граница х 1 =13,73 лет. 108

Показательно, что коэффициент вариации средней продолжительности обучения занятого населения составляет всего 1,45%, что свидетельствует о существенном выравнивании регионов ЦФО по показателям образования. Это говорит и в пользу модифицированного алгоритма расчета функции желательности: вряд ли целесообразно половину регионов считать аутсайдерами, достаточно выделить относительных лидеров и аутсайдеров (абсолютный лидер нами уже определен – это г. Москва, не вошедшая в однородную выборку регионов ЦФО). Судя по диаграмме Парето на рисунке 1 б , относительными лидерами в ЦФО являются Московская, Орловская и Смоленская области, относительными аутсайдерами – Ивановская, Владимирская и Тамбовская области.

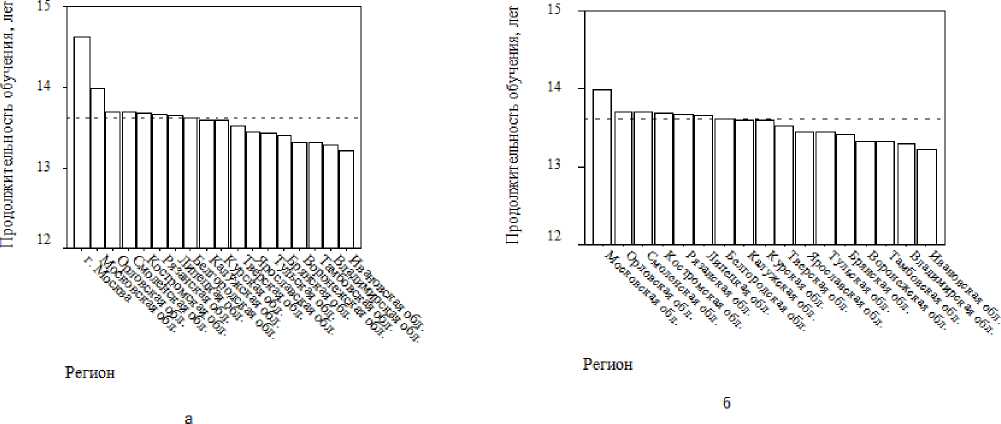
Рисунок 1 – Ранжирование регионов ЦФО по продолжительности обучения (рассчитано авторами по [18]): а – полная выборка; б – однородная выборка (без Москвы). Пунктир – среднее по РФ в целом (данные 2013 г.)

Формула (2) в модифицированном алгоритме имеет следующий вид:

z i = 0,5 + ( х i – х i ср )/( х i 1 – х i 0 ) = 0,5 + ( х i – х i ср )/(2 СКО( х i )),

где хi0 и хi1 – нижняя и верхняя границы зоны «удовлетворительно» определяются по формулам хi0= хiср – СКО(хi), хi1= хiср + СКО(хi).                                     (5)

где х i ср – среднее арифметическое (невзвешенное) по однородной региональной выборке,

СКО( х i ) – стандартное отклонение.

Для расчета значений кодированных переменных и функции желательности нами использовалась версия SPSS Base 8.0 для Windows [19].

Принцип построения функции желательности и ее график в именованных координатах показаны на рисунке 2. Как следует из рисунка 2 а , для построения частных функций желательности достаточно задаться двумя «реперными» точками – нижней и верхней границ зоны «удовлетворительно». Но это не является препятствием для выделения не трех зон желательности («плохо», «удовлетворительно», «хорошо»), как показано на рисунке 2 а , а пяти – «очень плохо», «плохо», «удовлетворительно», «хорошо», «очень хорошо» – рисунок 2 б .

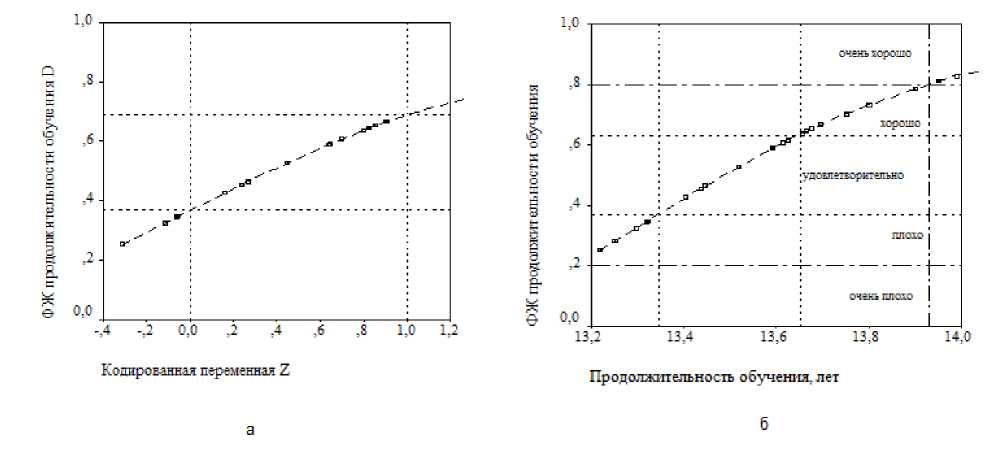
Рисунок 2 – Функция желательности средней продолжительности обучения: а – принцип построения; б – назначение зон желательности (данные 2013 г.)

Важно отметить, что функция желательности имеет сигмоидальную форму и отвечает условию (1). Сигмоидальный характер означает, что на начальном участке, в зоне желательности «плохо», функция имеет нарастающую кривизну, и рост показателя приводит к заметному увеличению желательности. Напротив, в зоне «хорошо» функция имеет убывающую кривизну, дальнейший рост показателя уже не вызывает столь заметного увеличения желательности, что полностью соответствует экономическому закону предельной полезности. В зоне «удовлетворительно», однако, функция желательности практически линейна, и именно в этой области наблюдается максимальный эффект от увеличения показателя.

Такой сигмоидальный характер зависимости желательности от величины показателя отвечает нашим интуитивным представлениям: на начальном этапе (зона «плохо») важно «поощрить» рост показателя, хотя бы это и было связано со значительными затратами ресурсов разного рода, а когда значения показателя нас уже устраивают (зона «удовлетворительно»), нет особого смысла в дальнейшем его росте (зона «хорошо»), поскольку затраты при этом резко увеличиваются. Практическое значение имеет также и то, что преобразование исходных показателей с использованием психофизической шкалы Харрингтона позволяет производить расчеты частных индексов для территорий, не включенных ранее в обучающую выборку – в данном случае, для Москвы.

Результаты ранжирования регионов ЦФО по значениям функции желательности средней продолжительности обучения занятого населения и их отнесения к зонам желательности приведены в таблице 2.

Таблица 2. Распределение регионов ЦФО по зонам желательности средней продолжительности обучения занятого населения

Зона желательности	Границы зоны, лет	Регионы, вошедшие в зону (перечислены в порядке возрастания показателя)
Плохо	13,15 … 13,45	Ивановская, Владимирская, Тамбовская, Воронежская области
Удовлетворительно	13,45 … 13,65	Брянская, Тульская, Ярославская, Тверская, Курская, Калужская, Белгородская области
Хорошо	13,65 … 13,93	Липецкая, Рязанская, Костромская, Смоленская, Орловская области
Очень хорошо	Более 13,93	Московская область, г. Москва

Аналогичным образом построены функции желательности двух других региональных показателей качества жизни – ожидаемой продолжительности жизни при рождении и уровня бедности, в качестве которого принята доля населения с доходом меньше прожиточного минимума. Первый из них отражает компоненту регионального ИРЧП «здоровье», второй – благосостояние населения, с учетом неравномерности распределения доходов.

Ранжирование регионов ЦФО по этим показателям, в соответствии с данными 2013 г., представлено на рисунке 3.

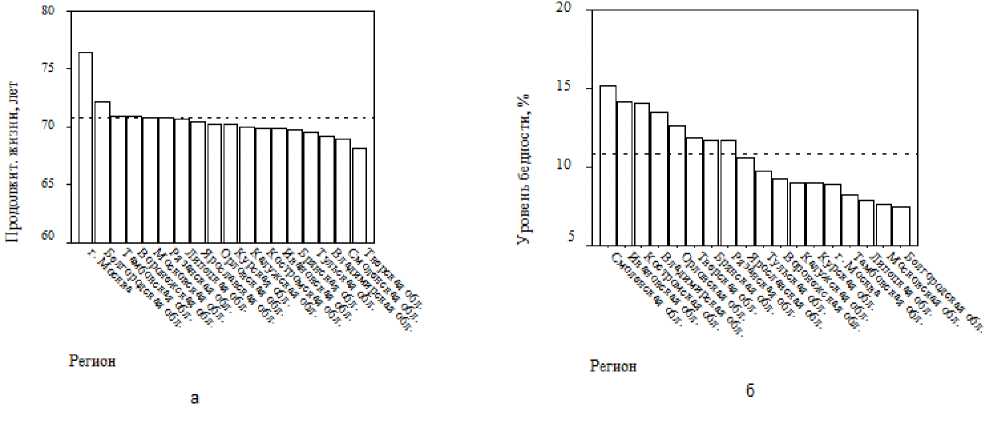
Рисунок 3 – Ранжирование регионов Центрального федерального округа по ожидаемой продолжительности жизни при рождении ( а ) и уровню бедности ( б ). Пунктир – уровень Российской Федерации (данные 2013 г.)

Дадим комментарий к рисунку 3. Из диаграммы Парето, представленной на рисунке 3 а, следует, что Москву с экстремально высоким значением ожидаемой продолжительности жизни при рождении следует исключить из однородной выборки регионов Центрального федерального округа, и функцию желательности ожидаемой продолжительности жизни при рождении необходимо строить без учета данных по этому региону. В отношении уровня бедности такого ограничения нет: уровень бедности населения Москвы больше, чем в четырех регионах Центрального федерального округа – в Белгородской, Московской, Липецкой и Тамбовской областях. Но уровень бедности – негативный показатель, для которого нижняя и верхняя границы зоны «удовлетворительно» определяются по несколько иным формулам хi0= хiср + СКО(хi), хi1= хiср – СКО(хi).                    (6)

где х i ср – среднее арифметическое (невзвешенное) по однородной региональной выборке,

СКО( х i ) – стандартное отклонение. Кодированные значения негативных показателей определяются также иначе:

z i = 0,5 – ( х i – х i ср )/(2 СКО( х i )).                         (7)

Ниже на рисунке 4 представлены графики функций желательности ожидаемой продолжительности жизни при рождении и уровня бедности. Видно, что основная масса точек-регионов сосредоточена в зоне «удовлетворительно», и меньшая их часть – в зонах «плохо» и «хорошо».

По аналогии с таблицей 2, представим распределение регионов Центрального федерального округа по зонам желательности ожидаемой продолжительности жизни при рождении (таблица 3) и уровня бедности (таблица 4).

В таблицах 2-4 обращает на себя внимание тот факт, что г. Москва, лидирующая по средней продолжительности обучения занятого населения и ожидаемой продолжительности жизни при рождении, по уровню бедности находится в зоне «удовлетворительно». Симптоматично, что, несмотря на высокие показатели доходов населения в среднем, в этом регионе имеется значительная часть населения с доходами ниже прожиточного минимума.

Отсюда следует, что при формировании обобщенного индикатора благосостояния, необходимо обратить самое пристальное внимание на показатели неравномерности распределения доходов среди населения.

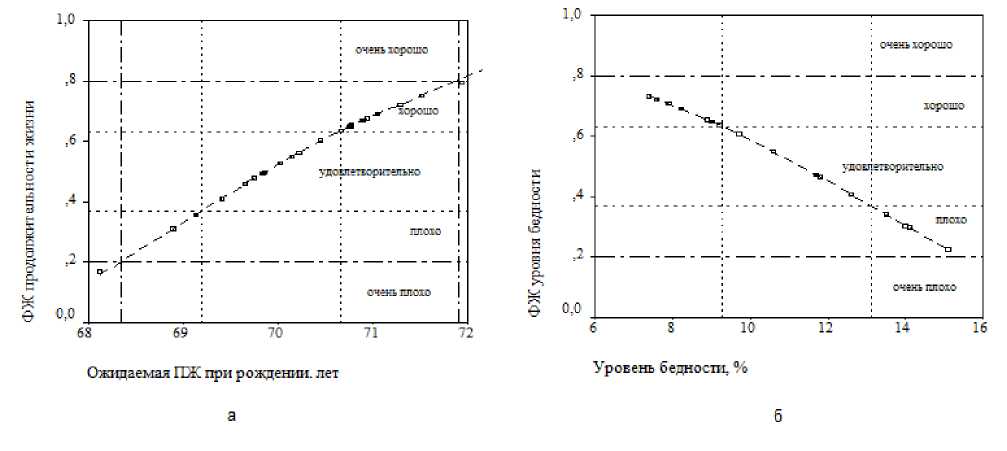
Рисунок 4 – Функции желательности ожидаемой продолжительности жизни при рождении ( а ) и уровня бедности ( б ). Данные 2013 г .

Таблица 3. Распределение регионов ЦФО по зонам желательности ожидаемой продолжительности жизни при рождении

Зона желательности	Границы зоны, лет	Регионы, вошедшие в зону (перечислены в порядке возрастания показателя)
Очень плохо	Менее 68,35	Тверская область
Плохо	68,35 … 69,20	Смоленская, Владимирская области
Удовлетворительно	69,20 … 70,65	Тульская, Брянская, Ивановская, Костромская, Калужская, Курская, Орловская, Ярославская области
Хорошо	70,65 … 71,90	Липецкая, Рязанская, Московская, Воронежская, Тамбовская области
Очень хорошо	Более 71,90	Белгородская область, г. Москва

Таблица 4. Распределение регионов ЦФО по зонам желательности уровня бедности

Зона желательности	Границы зоны, %	Регионы, вошедшие в зону (перечислены в порядке убывания показателя)
Плохо	Более 13,1	Белгородская, Московская, Липецкая, Тамбовская области
Удовлетворительно	13,1 … 9,3	г. Москва, Калужская, Курская, Воронежская, Тульская, Ярославская, Брянская, Рязанская, Тверская, Орловская области
Хорошо	Менее 9,3	Владимирская, Костромская, Ивановская, Смоленская области

В данной публикации мы не останавливаемся на вопросе формирования обобщенного индикатора качества жизни на региональном уровне – это предмет специального обсуждения. Тем не менее, обращает на себя внимание, что функции желательности продолжительности обучения и уровня бедности значимо не коррелируют друг с другом, а функции желательности уровня бедности и ожидаемой продолжительности жизни при рождении хотя и коррелируют между собой, но не дублируют друг друга. Отсюда следует, что свертка частных функций желательности в обобщенный индикатор качества 112

жизни будет носить достаточно сложный характер. В любом случае, помимо обобщенного индикатора, для всесторонней характеристики регионов Центральной России необходимо рассматривать все три стороны качества жизни – образование, здоровье и материальное благополучие населения.