О новом подходе к формированию сигнально-кодовых конструкций с высокой спектральной эффективностью

Постановка задачи

Увеличение потребности абонентов в информационном обмене независимо от их местоположения привело к интенсивному развитию и внедрению беспроводных систем передачи информации (БСПИ), однако в настоящее время возникла ситуация, когда радиочастотный ресурс для них практически исчерпан. Поэтому дальнейшее увеличение скорости передачи информации посредством БСПИ не представляется возможным – хотя спрос мобильных пользователей на современные мультисервисные услуги с требуемым высоким качеством обслуживания непрерывно возрастает. В связи с этим все более актуальной становиться проблема повышения эффективности БСПИ – как существующих, так и проектируемых в настоящее время. Эта проблема носит системный характер, так как, с одной стороны, обусловлена необходимостью повышения спектральной эффективности БСПИ, а с другой стороны, требует обеспечение заданного уровня достоверности передаваемой информации [1-2].

Среди известных способов решения указанной проблемы наиболее перспективны считается применение спектрально-эффективных сигнально-кодовых конструкций (СКК) на основе ортогональных сигнальных базисов OFDM (Ortogonal Frequency Division Multiplex), которые нашли практическое применение в современных БСПИ типа Wi-Fi, WiMAX, LTE [3-5]. Но достичь потенциально возможную спектральную эффективность в этих системах при использовании указанных сигнально-кодовых конструкций не удается, так как в них в качестве модулирующих используются импульсы с прямоугольной формой, что не позволяет достичь максимальной концентрации энергии в заданном частотном интервале [6].

Авторами для решения указанной проблемы предлагается новый оригинальный метод построения СКК, обеспечивающих, при заданных ограничениях на частотно-временные ресурсы канала радиосвязи, максимальную спектральную эффективность БСПИ [7]. Суть метода заключается в использования нового ортогонального сигнального базиса вместо базиса Фурье, применяемого в настоящее время для формирования СКК.

Математические основы

Пусть s ( t ) передаваемый сигнал, в параметрах которого закодированы передаваемые символы из многоосновной системы модуляции d_k , а u ( t ) сигнал на выходе канала связи.

В предположении линейности и инвариантности параметров канала во времени эти сигналы связаны следующим соотношением:

Т,.

u(t) = ^s(T)-h(t — T)dr Ze[o,T_;J; (1)

где h ( t – τ ) – импульсная характеристика канала связи; Т_с – длительность сигнала s ( t ); Т_р – длительность сигнала на выходе канала u ( t ); [ T_c , T_p ] – интервал времени рассеивания, когда сигнал на выходе канала имеет энергию, достаточную для возникновения межсимвольной интерференции.

К СКК предъявляется требование в виде неизменности формы передаваемого сигнала при передаче через ограниченный частотно-временными ресурсами канал:

данного уравнения h ( t – τ ). Ядро этого уравнения является эрмитовым, поэтому его собственные числа вещественные.

Заметим, что все собственные функции ядра (5) удовлетворяют условию (2). Однако так как предполагается передача J символов, то одной собственной функции для этого недостаточно, поэтому сигнал целесообразно представить в виде линейной комбинации:

u(f) « к • s(t), ?g[O,T_c]

Для выполнения требования (2) сигнал s ( t ) должен быть согласован с импульсной характеристикой h ( t – τ ) и передаточной характеристикой H ( ω ) канала [8].

Предполагается, что информация передается по каналу связи, частотный интервал которого ограничен и определяется соотношением

Q =[Q₁,Q₂]; Q, = 2nv_k, к = 1,2 ;   (3)

Δ F = v ₂ – v ₁. Пусть в этой области выполняется условие для H ( ω ):

to e Q ; to £ Q.

Тогда импульсная характеристика определяется следующим образом:

s^ = y,d_kg_k^tY (7)

где d_k – передаваемые символы в общем случае комплексные; g_i ( t ) – собственные функции ядра (5) системы.

Для выполнения условия (2) необходимо и до статочно выбирать собственные функции с одинаковыми собственными числами λ ₁ = λ ₂ = … = λ ≈ 1, при этом значение собственного числа характеризует степень концентрации энергии собственной функции в заданном частотном интервале [10].

Так как предполагается использование для формирования сигнально-кодовых конструкций средств вычислительной техники, которые работают с дискретными последовательностями, ядро (5) необходимо дискретизовать. В таком случае оно представимо в виде матрицы А с элементами вида (субполосной матрицы):

И^_^ = — \eja(t^dto = gj^iU-t^ _eJn^t-^

j^(t - r) ’

Q.,k

]2тг(1-к)

V2-V1

при i*k;

при i = k;

где 7 = (-l) . В соответствии с требованием (2) выражение (1) принимает вид

Tc к s(t)= s(T)-h(t-T)dr,

о

V. = V, = 2nv,; v, = kAt; V₃ = 2^v, .

Таким образом, задача вычисления базисных функций может быть сведена к вычислению собственных векторов q_i ( t ) и собственных чисел λ_i матриц вида (8).

Для заданной последовательности передаваемых модуляционных символов d_k выполняется умножение на собственные векторы матрицы (8) согласно выражению

Тогда согласованность сигнала s ( t ) с импульсной характеристикой канала может быть выполнена, в случае если s ( t ) будет являться собственной функцией линейной системы с импульсной характеристикой h ( t – τ ) [9].

Таким образом, (6) представляет собой интегральное уравнение с ядром вида (5). Как известно, решение данного уравнения может существовать в виде собственных функций g_i ( t ) и соответствующих им собственных чисел λi ядра

5 = E dkQk = k=\                                              (9)

После этого спектр полученного вектора переносится на несущую частоту в квадратурном модуляторе и сформированная СКК передается в канал связи.

Результаты компьютерного моделирования. Оценка спектральной эффективности

Для оценки спектральной эффективности γ использовалось следующее выражение:

R

Y"^’               (10)

где R = J / T_c – скорость передачи информации; Δ F – ширина полосы частот, занимаемая сигналом. Формирование и обработка СКК осуществлялась в системе Matlab. Моделирование осуществлялось следующим образом:

Генерировалась бинарная случайная последовательность, которая являлась передаваемыми данными. Из полученной бинарной последовательности формировались модуляционные символы d_k вида QAM. Далее формировались сигнально-кодовые конструкции для двух смежных каналов шириной полосы 20 МГц и длительностью 12,8 мкс с использованием классического OFDM (на основе базиса Фурье (БФ)) и собственных векторов матриц (8) (СВМ). Значения несущих частот были следующими: канал 1 – 2,48 ГГц; канал 2 – 2,5 ГГц.

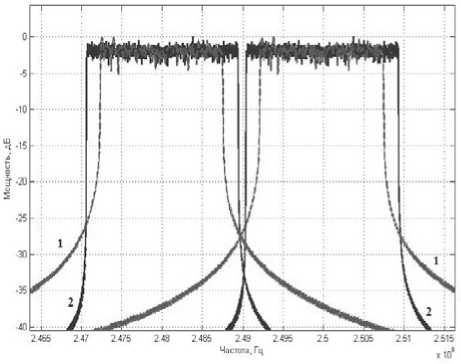
Рис. 1. Спектральные плотности сигналов 1) базис Фурье; 2) базис собственных векторов матриц (11)

На рис. 1 показаны усредненные значения спектральной плотности СКК БФ (кривая 1) и спектральной плотности СКК СВМ (кривая 2), полученные в результате компьютерного моделирования. Величина спада частотного спектра сигнала за выделенным частотным диапазоном определяет уровень межканальной интерференции. Так как величина спада спектральной плот- ности СКК СВМ гораздо выше, чем в OFDM, а ширина окна канала фиксирована (в данном случае 20 МГц), то появляется возможность уменьшить величину вводимых защитных интервалов между смежными каналами связи и увеличить за счет этого спектральную эффективность γ (см. рис. 1), при этом уровень МКИ остается ниже, чем в СКК с БФ.

Возникает необходимость оценить способность предлагаемого подхода формировать СКК с заданными свойствами при различных комбинациях Δ F и Т_с . С этой целью проводился эксперимент, в котором менялись значения ширины частотного диапазона Δ F при разных значения длительности сигнала и вычислялись собственные векторы матрицы (8). Потом проводилась выборка собственных векторов, собственные числа которых имеют значение λ ≈ 1, и считалось их количество.

В таблице 1 приводятся результаты экспериментов по сравнительной оценке количества субполосных базисных функций в заданных частотно-временных ресурсах канала связи. В полях таблицы представлены отношения количества допустимых к использованию базисных функций при использовании СКК СВМ к числу функций в базисе Фурье.

Таблица 1. Относительные числа формируемых базисных функций

Tc, мкс	Ширина частотного диапазона, МГц
	1,25	2,5	5	10	20
25,6	1,24	1,24	1,24	1,23	1,23
12,8	1,25	1,24	1,24	1,24	1,23
6.4	1,16	1,25	1,24	1,24	1,24
3,2	1	1,16	1,25	1,24	1,24
1,6	1	1	1,16	1,25	1,24

Из результатов, приведенных в таблице 1, можно сделать вывод, что заметное преимущество (порядка 20%) предлагаемого подхода формирования СКК перед классическим базисом Фурье, с точки зрения количества используемых базисных функций с заданными свойствами, наблюдается при условии T_CNF>%.

Результаты оценки спектральной эффективности γ исследуемых сигнально-кодовых конструкций представлены в таблице 2.

Таблица 2. Спектральная эффективность сигнальнокодовых конструкций

Вид модуляции	Вид базиса
	Базис Фурье	Базис CBM
QAM-4	1,57	1,96
QAM-16	3,14	3,9
Q AM-64	6,28	7,78

Данные значения были рассчитаны исходя из предположения, что полоса, занимаемая сигналом, составляет 20 МГц, длительность сигнала 12,8 мкс.

Таким образом, проведенный эксперимент доказывает, что предлагаемый класс сигнальнокодовых конструкций обладает спектральной эффективностью на 20% большей, чем сигналы, сформированные с использованием базиса Фурье, при одинаковых выделенных частотно-временных ресурсах канала связи.

Оценка энергетической эффективности

Для вычисления энергетической эффективности использовалось выражение вида:

/? = 101og10

Г R

где R – скорость передачи информации за Т_с ; ρ₀ – отношение энергии сигнала E_s к спектральной плотности N₀ шума в полосе Δ F .

Для оценки энергетической эффективности β проводились вычислительные эксперименты с использованием компьютерного моделирования по оценке вероятности ошибочного приема при заданной интенсивности шума в канале связи.

Необходимо отметить, что обработка сигнала осуществлялась в виде вычисления оценок модуляционных символов в виде скалярных произведений согласно выражению

_ N dk=y4Sn-qk.,^ k = \;2...J, (12)

где d_k – восстановленная последовательность модуляционных символов; q_{k , n} – собственные векторы матрицы (8); d, – принятый из канала связи сигнал, прошедший через квадратурный демодулятор.

Полученные значения d j обрабатываются решающим устройством, при этом принятие решений заключается в поиске такого d_i , для которого выполняется условие

|Ret/,. -Ке^| + |1т,. -Imt/A.| =

= min Ret/,,, -Ret/J + Imt/,„ -Imt/J , (13)

1 < z < тп, к = \...J, где dk – принятый символ; di – искомый символ алфавита; dm – эталонные символы.

При этом в качестве модели шума используется белый гауссовый шум, энергия которого равномерно распределена в частотной области с нулевым математическим ожиданием. Значение P_ош вычислялось согласно следующему выражению:

P_ош = L_ош / L ,

где L – число переданных информационных бит; L_ош – число ошибочно принятых бит; при этом выполнялось соотношение: L ≥ 10⁶ и результаты усреднялись по серии из пяти экспериментов. Результаты расчетов приведены на графиках рис. 2. Результаты оценки энергетической эффективности исследуемых сигналов представлены в таблице 3.

По итогам вычислительных экспериментов удало сь установить, что предлагаемый класс СКК обладает энергетической эффективностью на 0,8 дБ большей, чем СКК, сформированные с использованием базиса Фурье, при одинаковых выделенных частотно-временных ресурсах канала. Здесь также необходимо отметить, что повышение энергетической эффективности будет выполняться при условии T_C^F> 8.

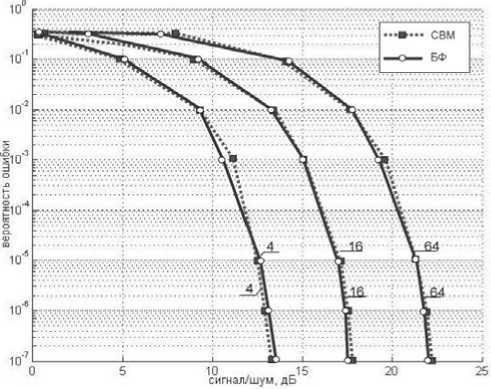
Рис. 2. Вероятность ошибки на бит (BER) СКК БФ и СВМ

Таблица 3. Энергетическая эффективность сигнальнокодовых конструкций

Вид модуляции	Вид базиса
	Базис Фурье, дБ	Базис СВМ, дБ
QPSK	13,11	13,92
QAM-16	10,05	10,85
Q AM-64	8,12	8,93

Выводы

В результате проведенных исследований установлено, что предлагаемый класс сигнально-кодовых конструкций на основе собственных векторов субполосных матриц не только превосходит на 20% сигнально-кодовые конструкции на основе базиса Фурье по спектральной эффективности, но и одновременно с этим обладает на 0,8 дБ большей энергетической эффективностью.

Эти показатели характерны для сигнально-кодовых конструкций, частотно-временные значения которых удовлетворяют условию Tc-AF > 8. Данный факт позволяет утверждать, что применение данных сигналов в высокоскоростных широкополосных системах связи позволит повысить эффективность работы системы связи в целом, а также обеспечить большую скорость передачи информации между абонентами.

Исследования выполнены при поддержке РФФИ, проект № 12-07-00514-а на тему: «Минимизация затрат ресурсов информационно-телекоммуникационных систем (ИТС) при хранении и передаче речевых данных на основе примене- ния оптимальных методов и алгоритмов их обработки» и Государственного задания НИУ БелГУ на 2014 г. (проект № 358).