О новом подходе в математическом прогнозировании водонепроницаемости цементных композитов
Автор: Королев Александр Сергеевич
Рубрика: Строительные материалы, изделия и конструкции
Статья в выпуске: 25 (125), 2008 года.
Бесплатный доступ
Работа посвящена раскрытию новой закономерности формирования водонепроницаемости структуры цементных композитов от основных факторов состава с учетом фактора неоднородности строения матричного компонента.
Цементные композиты, водонепроницаемость, прогнозирование гидратной структуры, радиус макрокапилляров
Короткий адрес: https://sciup.org/147154201
IDR: 147154201 | УДК: 666.97
Текст научной статьи О новом подходе в математическом прогнозировании водонепроницаемости цементных композитов
В настоящее время в современном материаловедении не существует адекватных математических моделей прогнозирования водонепроницаемости цементных композитов, что сдерживает выработку обобщенных методов подбора составов цементных смесей с заданной водонепроницаемостью в различные сроки твердения.
По результатам ранее проведенных исследований были получены следующие результаты, яв ляющиеся основанием для моделирования водонепроницаемости бетона.
Система макрокапилляров цементных композитов непрерывна и является межкристаллитным образованием в структуре цементного камня. Фактическое строение макрокапилляров является неточным цилиндрическим, расчетное строение -цилиндрическое с приведенным гидравлическим радиусом (рис. 1).
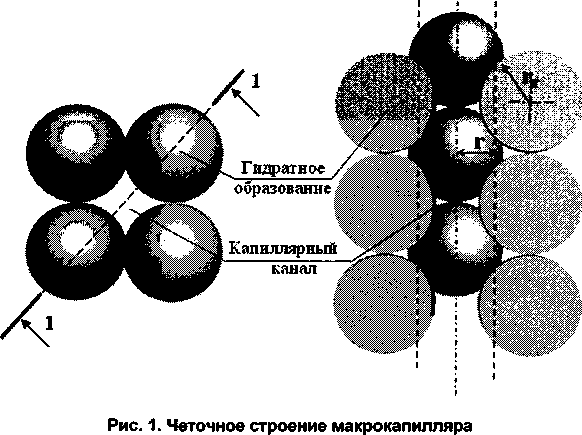
Образование макрокапилляров обусловлено топологическими особенностями формирования гидратной структуры цементного камня:
-кристаллизацией гидратных новообразований вблизи поверхности цементного зерна с образованием микроскопических кластерных образований с упорядоченной структурой и неплотной упаковкой;
-
— наличием свободной влаги, защемленной между кристаллитными образованиями, не участвующей в гидратации цемента и разуплотняющей упаковку макроскопических гидратных образований;
-
- неплотностью гидратных микроскопических кластерных образований, которые являются субмикрокристаллической фазой, содержащей микро-капиллярную и гелевую пористость, способную адсорбировать или физико-химически связывать свободную влагу.
Макрокапилляры обладают одним размерным порядком с кластерными гидратными образованиями цементного камня. Формирование структуры цементного камня в виде кластерных образований связано с накоплением продуктов гидратации в виде значительных субмикрокристаллических образований размером более 10 мкм. Кристаллизация таких скоплений происходит на протяжении времени с поверхности вглубь с длительным сохранением определенного количества незакри-сталлизованной фазы. С этих позиций микропоры являются внутрикластерным образованием. Фактическое и расчетное строение субмикрокристаллических кластерных образований - сферолиты с приведенным радиусом. На этом основании предложена сферолитно-решеточная расчетная модель структуры цементного камня (см. рис. 1).
Снижение влагопереноса по макрокапиллярам под действием капиллярных сил или гидростатического давления при уплотнении гидратной структуры связано с возрастанием вязкости воды в пристеночных слоях при уменьшении гидравлического радиуса макрокапилляров и, как следствие, увеличением силы трения о стенки капилляров. С этих позиций аналитически получен и экспериментально апробирован новый показатель водонепроницаемости цементных композитов - удельное гидравлическое сопротивление (t), зависящее от гидравлического радиуса макрокапилляров (г), поверхностного натяжения проникающей жидкости (<т ) и угла смачивания проникающей жидкостью ( У ) стенок капилляров.
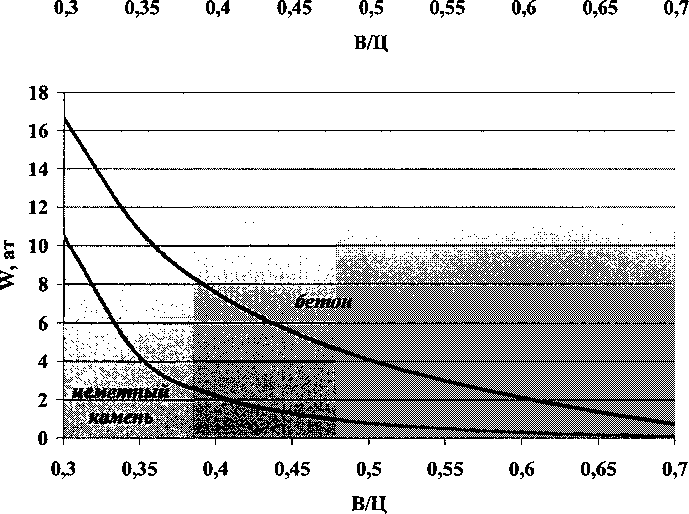
2 г/г,. Критериями плотности структуры цементного камня являются: радиус макрокапилляров и геометрическая плотность. Радиус макрокапилляров -есть критериальная характеристика, объединяющая в себе несколько параметров структуры: объем макрокапиллярных пор, удельную поверхность и плотность кристаллитных кластерных образований. Геометрическая или структурная плотность -отношение радиуса макроскопических кластерных гидратных образований и порядка структурной решетки. Определена математическая взаимосвязь между гидравлическим радиусом макрокапилляров цементных композитов и показателями высоты капиллярного поднятия влаги ^=0,0394-1012 г2. (2) Таким образом, после подставления выражения высоты капиллярного поднятия и поверхностного натяжения воды получим г подставляется в мк. Аналитически определена математическая зависимость между показателями макропористости и геометрической плотности цементных материалов, позволяющая оценивать размерный порядок гидратных кластерных образований в макроструктуре цементного камня. у = —— = cos^jp . (4) г+ гг Для математического моделирования водонепроницаемости была предложена физическая модель выделенного макрокапилляра, согласно которой водонепроницаемость цементного композита равна водонепроницаемости одного выделенного в структуре макрокапилляра. Для марочной водонепроницаемости: W = 15-1^ =1^X5-^, (5) где 0,15 - высота стандартного образца (м) при определении марки по водонепроницаемости. ^ = 36^3/о,15о, 04г2), (6) г подставляется в мк. Следовательно, основным показателем, определяющим водонепроницаемость цементных композитов, является гидравлический радиус макрокапиллярных пор. Выразим радиус макрокапилляров г через показатель структурной плотности цементного камня по (4): где гг — средневзвешенный радиус гидратированных частиц цемента, примем данный радиус, равным радиусу исходных частиц цемента; Р - макропористость цементного камня, по [1] В/Ц-0,42а " 0,32 + В/Ц ’ р_ 0,58В/Ц-0,12 ” 0,32 + В/Ц ' Результатом коррелирования зависимости (7) с фактическими данными радиуса макрокапилляров, определенного по капиллярному поднятию влаги является зависимость 1 COS^fP -1 Данная зависимость (рис. 2) демонстрирует очень хорошую сходимость (коэффициент корреляции 0,98). Заполнитель в цементных композитах способствует проявлению синергетического эффекта композиционного самоуплотнения - образованию структуры цементного камня с переменной пористостью в направлении от центра матричной прослойки к поверхности заполнителя, что способствует увеличению геометрической плотности и непроницаемости композита в целом при соблюдении определенных условий. Наблюдаемый эффект связан с поверхностными адсорбционными силами запол нителя, которые приводят к переменному распределению водосодержания по толщине матричной прослойки, поэтому механизм данного явления можно назвать гидравлическим самоуплотнением. Переменность структуры матричного компонента приводит к интегральному эффекту повышения прочности и непроницаемости композита. Получена математическая зависимость прироста прочности и водонепроницаемости структуры от степени неравномерности распределения водосодержания по толщине матричной прослойки -функции поверхностного влияния заполнителя. ^гс £пс (В/Ц-0,2)3 (НГ-0,2)3 ’ где коэффициент плотного слоя составляет Апс = 1-cos 1,57 НГ-0,2 "I В/Ц-0,2 J (Ю) Гидравлическое самоуплотнение наиболее эффективно проявляется при В/Ц-отношениях менее критического значения, соответствующего водоудерживающей способности композиционной сме си. Предложена математическая зависимость критического В/Ц от показателей водопотребности компонентов композитной смеси. Повышение гидрофильности заполнителя и снижение водопотребности вяжущего при прочих равных условиях приводит к уплотнению структуры, т. е. повышению водонепроницаемости и прочности, что свидетельствует о положительном влиянии переменности матричного компонента на свойства композита. Поэтому при расчете водонепроницаемости цементных композитов следует учитывать эффект гидравлического самоуплотнения. ^ = £„^^(0,15-0,04г2), (11) где krc - коэффициент гидравлического самоуплотнения, определяемый по выражению (9) Проверка точности при определении водонепроницаемости бетонов (табл. 1) показала коэффициент корреляции 0,85, в 95 % случаях обеспечивается точность в пределах марки по водонепроницаемости. Зависимость водонепроницаемости бетона от В/Ц на Коркинском цементе представлена на рис. 3. Таким образом, гидравлический механизм самоуплотнения может быть усилен путем введения поверхностно-активных веществ: при обработке поверхности заполнителя регуляторами смачивания и введении пластифицирующих добавок без снижения В/Ц бетонной смеси. Повышение гидрофильности зерен заполнителя улучшает прочностные показатели на 10... 15 % и водонепроницаемость композита на 40...50 % при прочих равных условиях Основным условием самоуплотнения при введении пластифицирующих добавок является сохранение подвижности бетонной смеси. В этом случае дополнительное синергетическое уплотнение позволяет повысить прочность на 10... 15 % и водонепроницаемость в 2 и более раз. Уровень прироста водонепроницаемости при введении пластификаторов определяется по (12) Рис. 2. Зависимость радиуса макрокапилляров цементного камня от В/Ц Таблица 1 5 О ш § ° СО О S Марка цемента В/Ц нг, % Макро-пористость, Р Радиус макрокапилляров, г, мкм Коэф, уплотненного слоя, ^пс Коэф, гидравлич. самоуплотнения, ^гс w гг раем? ат rr факт» ат Отклонение от факт., % ж S К о яс ПЦ500Д0 0,36 25 0,13 1,02 0,12 3,87 14,24 13,50 5,4 0,5 0,21 1,45 0,03 7,35 5,77 6,00 -3,8 0,71 0,28 1,86 0,01 12,55 0,86 0,88 -2,6 ПЦ400Д20 0,36 25 0,13 1,02 0,13 3,67 13,53 14,00 -3,4 0,5 0,21 1,45 0,04 7,00 5,49 5,50 -0,2 0,71 0,28 1,86 0,01 11,95 0,82 0,75 8,8 ШПЦ400 0,36 25 0,13 1,02 0,10 4,31 15,88 14,50 9,5 0,5 0,21 1,45 0,03 8,18 6,42 5,50 16,7 0,71 0,28 1,86 0,01 13,95 0,95 0,85 12,1 « S id Ct 1 о яс CL гО ПЦ500Д0 0,35 "0,5 28 0,12 0,99 0,29 2,34 9,97 11,20 -11,0 0,21 1,45 0,08 4,87 3,82 5,70 -33,0 0,71 0,28 1,86 0,03 8,34 0,57 0,64 -10,9 ПЦ400Д20 0,36 29 0,13 1,02 0,33 2,19 8,06 8,00 0,7 0,5 0,21 1,45 0,10 4,28 3,36 3,50 -4,1 0,71 0,28 1,86 0,03 7,35 0,50 0,60 -16,3 >52 S О S а Си О Ы ПЦ500Д0 0,36 25 0,13 1,02 0,12 3,87 14,24 12,90 10,4 0,5 0,7 Г 0,21 1,45 0,03 7,35 5,77 4,50 28,2 0,28 1,86 0,01 12,55 0,86 0,80 7,2 ПЦ400Д20 0,36 25 0,13 1,02 0,11 4,08 15,01 11,70 28,3 0,5_ 0,71 _ 0,21 1,45 0,03 7,74 6,08 5,80 4,8 0,28 1,86 0,01 13,21 0,90 0,90 0,3 ШПЦ400 0,36 26 0,13 1,02 0,17 3,19 11,76 10,80 8,9 0,5 0,21 1,45 0,05 6,11 4,80 4,00 19,9 0,71 0,28 1,86 0,02 10,45 0,71 0,65 9,8 Ж § * о е; о X о ПЦ500Д0 0,36 24 0,13 1,02 0,07 5,20 19,15 20,00 -4,3 0,5 0,21 1,45 0,02 9,83 7,71 6,40 20,5 0,71 0,28 1,86 0,01 16,74 1,14 1,10 4,0 ПЦ400Д20 0,36 26 0,13 1,02 0,18 3,06 11,26 11,80 -4,6 0,5 0,21 1,45 0,05 5,86 4,60 4,50 2,2 0,71 0,28 1,86 0,02 10,03 0,69 0,70 -2,1 ШПЦ400 0,36 31 0,13 1,02 0,51 1,67 6,15 6,50 -5,4 _0,5 _ ' 0,7? 0,21 1,45 0,15 3,35 2,63 2,50 5,1 0,28 1,86 0,05 5,79 0,40 0,50 -20,8 ж S к о о яс св 00 Й к ПЦ500Д0 0,36 25 0,13 1,02 0,12 3,87 14,24 13,50 5,4 0,5 0,21 1,45 0,03 7,35 5,77 6,00 -3,8 0,71 0,28 1,86 0,01 12,55 0,86 0,85 0,9 ПЦ400Д20 0,36 25 0,13 1,02 0,13 3,67 13,53 12,10 11,8 0,5 0,21 1,45 0,04 7,00 5,49 5,76 -4,7 0,71 0,28 1,86 0,01 11,95 0,82 0,90 -9,3 ШПЦ400 0,36 25 0,13 1,02 0,10 4,31 15,88 12,50 27,0 _0,5 _ "0,71 0,21 1,45 0,03 8,18 6,42 6,80 -5,6 0,28 1,86 0,01 13,95 0,95 1,10 -13,4 (НГ-0,2)3 ((1-^д)нГ-0,2)3 1-COS 1,57 (l-^Hr-O^ В/Ц-0,2 НГ-0,2 В/Ц-0,2 где А^д - водоредуцирование при введении пла стификатора. Проверка точности расчетного определения прироста водонепроницаемости бетонов при введении водоредуцирующих добавок ЛСТ и С-3. Коэффициент корреляции имеет невысокое значение 0,73, однако предложенная зависимость позволяет более чем в 80 % случаев прогнозировать водонепроницаемость пластифицированных бетонов с точностью до марки. Для учета прироста водонепроницаемости при введении микродобавок применим зависимость (4) Рис. 3. Математическая модель водонепроницаемости (W, ат) бетона для ПЦ 400-Д20 Коркинского завода г 1 COSy/P -1 с учетом повышения дисперсности гидратной структуры средневзвешенный радиус гидратного образования снижается по зависимости _ тивгв + мдгд _ (1-ШдХ + тДгД Ку — — где тв и тй - массовые доли вяжущего и добав ки; гв и гд - средневзвешенные радиусы частиц вяжущего и добавки. Тогда г = кД—L=-ll (14) V COSy/P ) Прирост водонепроницаемости составит kw-Д (15) Ку Например, для микродобавки с размером частиц 5 мкм и дозировкой 10 % от массы цемента ( 2 5^ к =1-0,1 1—— = 0,94; Ч 7; к№=-Д = 1,2. 0,943 Для проверки зависимости был проведен эксперимент по введению в бетонную смесь с Ц/В = 2 на Коркинском ПЦ 400 Д-20 добавок с различными дозировками. Результаты (табл. 2) показывают очень высокую сходимость фактических и расчетных приростов водонепроницаемости. Таблица 2 Вид добавки Дозировка, % гд, мк к. ^факт Расч. kw Факт. kw Отклонение от факт., % Fe2O3 0 — 5,1 — — — 10 2,5 0,94 6,3 1,20 1,24 -3,0 20 0,87 8,2 1,52 1,62 -6,0 Метакаолин 0 — 5,6 — — 10 2,5 0,94 6,8 1,20 1,21 -0,3 20 0,87 8,5 1,52 1,52 — Тонкомолотый цемент 0 — 5,5 — — 10 4 0,96 6,0 1,13 1,09 3,4 20 0,91 7,5 1,33 1,36 -2,2 Выводы 1. Разработан математический закон водонепроницаемости, учитывающий в качестве основных факторов: гидравлический радиус макрокапилляров и эффект гидравлического самоуплотнения гидратной структуры. Также учитывается дисперсность вяжущего, поверхностное натяжение проникающей жидкости и угол смачивания стенок капилляров проникающей жидкостью. Полученная зависимость позволяет на основе характеристик материалов и состава цементного композита точно рассчитывать марку по водонепроницаемости. 2. Предложены математические основы прогнозирования уплотняющего действия микро- и нанодобавок, изменяющих активность вяжущего, учитываемую при определении прироста прочности, и дисперсность гидратной структуры, учитываемую при определении прироста водонепроницаемости. 3. Разработанные математические модели позволяют регулировать свойства цементных композитов, исходя из заданных условий эксплуатации, а также использовать потенциал заполнителя и добавок в целях повышения эксплуатационных свойств. За счет управления адсорбционной способностью заполнителей, вяжущего и добавок возможно обеспечение прироста водонепроницаемости в 4...5 раз.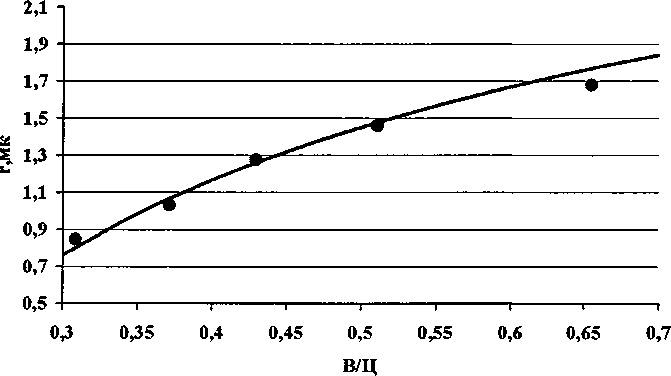
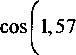

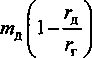
Список литературы О новом подходе в математическом прогнозировании водонепроницаемости цементных композитов
- Состав, структура и свойства цементных бетонов/под ред. Г.И. Горчакова. М.: Стройиздат, 1976. 45 с.
- Чеховский, Ю.В. Понижение проницаемости бетона/Ю.В. Чеховский. М.: Энергия, 1968. 192 с.


