О новом принципе интегрирующего аналого-цифрового преобразования с бестактовым поразрядным уравновешиванием

Неотъемлемой частью всех современных систем сбора и цифровой обработки данных являются аналого-цифровые (АЦП) и цифроаналоговые (ЦАП) преобразователи [1], от степени помехоустойчивости которых зачастую зависит достоверность результатов экспериментальных исследований. Это диктует необходимость применения в контрольно-измерительной и регистрирующей аппаратуре, работающей в условиях высокого уровня внешних помех, интегрирующих методов АЦП [2].

Классические АЦП с двухтактным интегрированием [2, 3] предназначены в основном для работы с низкочастотными процессами, так как для них характерна потеря информации об изменениях входного сигнала на втором такте преобразования, когда «интеграл» входного сигнала пре- образуется в цифровой код. Применение же параллельных и противофазно работающих АЦП, когда один канал интегрирует величину входного сигнала, а второй при этом преобразует предыдущий «интеграл» в цифру, влечет за собой значительное усложнение схемы АЦП и требует ее прецизионной настройки.

Число-импульсные интегрирующие АЦП [3, 4], несмотря на то что лишены базового недостатка АЦП с двухтактным интегрированием, связанного с потерями данных о входном сигнале, требуют высокоточных преобразователей «напряжение (ток) – частота» (ПНЧ), так как за тактовый интервал счета здесь происходит суммирование погрешности всех периодов выходных импульсов ПНЧ, приходящихся на тактовый интервал АЦП. В результате суммарная ошибка АЦП даже при высокоточном ПНЧ может оказаться недопустимо большой.

Если анализировать первопричину отмеченных недостатков АЦП, то она очевидна – существующие АЦП зачастую относятся к классу разомкнутых систем регулирования, где достижение высокой точности и помехоустойчивости является достаточно сложной задачей. Кроме того, большинство известных АЦП являются тактируемыми системами, где время преобразования задается дополнительным тактовым генератором, а определяется наиболее инерционным звеном в схеме АЦП.

Ниже рассматривается новый принцип построения замкнутого интегрирующего АЦП с бес-тактовым поразрядным уравновешиванием и встроенным в его замкнутый контур цифроаналоговым преобразователем (ЦАП). В дальнейшем обозначим данный преобразователь как АЦП – ЦАП.

В состав АЦП – ЦАП (рис. 1), прародителем которого являются многозонные интегрирующие развертывающие преобразователи [5, 6], входят сумматоры Σ ВХ , Σ 2n-1 … Σ 2n-3 и Σ ВЫХ , интегратор И с передаточной функцией W ( p )= 1/ Tp , где Т – постоянная времени интегрирования, релейные элементы РЭ1 … РЭ n , пропорциональные звенья П1 … П n , ключи Кл.1 … Кл. n , устройство вычитания кодов УВК и источник заранее заданного фиксированного кода ИК. При рассмотрении работы АЦП – ЦАП ограничимся четырьмя разрядами « n» двоичного кода.

Звенья Σ ВХ , Σ 2 n –1 , … , Σ 2 n –3 , И, РЭ1 … РЭ n , УВК и ИК в совокупности образуют АЦП. Функции ЦАП выполняют пропорциональные звенья П1 … П n и Σ ВЫХ .

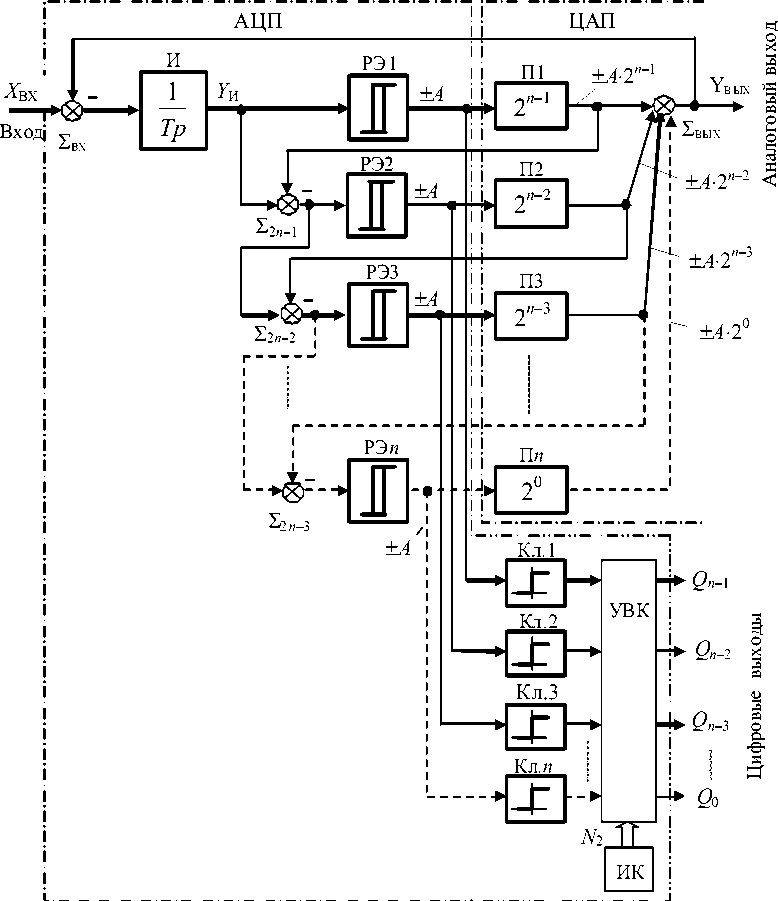
Рис. 1. Структурная схема замкнутого интегрирующего АЦП – ЦАП с бестактовым поразрядным уравновешиванием

Сумматоры Σ_ВХ, Σ_{2 n –1}… Σ_{2 n –3} имеют единичный коэффициент передачи по каждому из входов и производят вычитание входных сигналов. Релейные элементы РЭ1 … РЭ n в общем случае имеют симметричную относительно «нуля» петлю гистерезиса, а их выходной сигнал меняется дискретно в пределах ± А .

Ключи Кл.1 … Кл. n преобразуют биполярные выходные импульсы релейных элементов РЭ1 … РЭ n в однополярные для последующего согласования выходов релейных элементов РЭ1 … РЭ n с цифровыми входами УВК. Каждый из ключей Кл.1 … Кл. n имеет нулевое значение порогов включения / выключения и неинвертирующую характеристику «вход–выход».

Пропорциональные звенья П1 … Пn реализованы с коэффициентами передачи, которые изменяются в соответствии с весом разряда преобразуемого кода в общем случае с произвольным основанием, но чаще, как принято здесь, с двоичным кодом, пропорциональным 2n–1, 2n–2, … , 20. Наибольший коэффициент пропорционального звена 2n–1 соответствует весу старшего разряда двоичного кода, а наименьший 20 – весу младшего разряда.

УВК производит операцию поразрядного вычитания из кода N 1 , формируемого на выходе ключей Кл.1 … Кл. n , кода N 2 , задаваемого ИК, и может выполняться как на основе стандартных микросхем, так и на базе программируемых контроллеров.

На временных диаграммах сигналов преобразователя (рис. 2–5) и далее в тексте приняты следующие обозначения: Х _ВХ – входной сигнал; Y _И – выходной сигнал интегратора И; Y ВЫХ – выходной сигнал Σ ВЫХ ; ± А ⋅ 2 ^{n –1}, ± А ⋅ 2 ^{n –2}, ± А ⋅ 2 ^{n –3}, … , ± А ⋅ 2⁰ – максимальные уровни сигналов на выходе пропорциональных звеньев П1 … П n соответственно; ± b – пороги переключения РЭ1 … РЭ n ; ± А – амплитуда выходных импульсов релейных элементов РЭ1 … РЭ n ; Q n –1 , Q n –2 , Q n –3 , … , Q 0 – разряды циф-

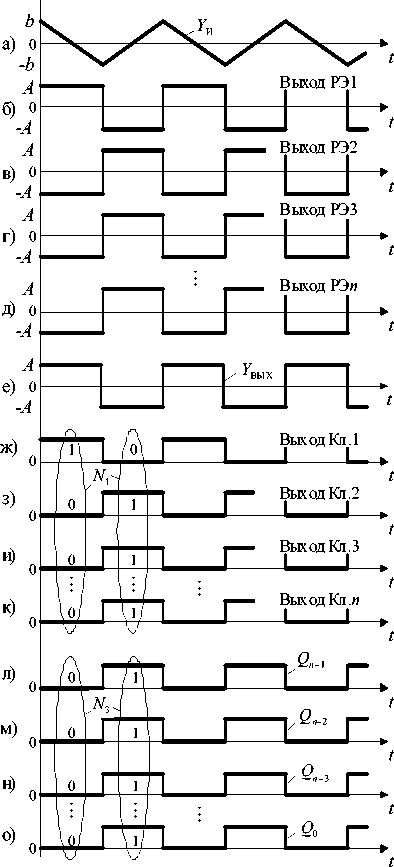
Рис. 2. Временные диаграммы сигналов интегрирующего АЦП – ЦАП при k = m = 0

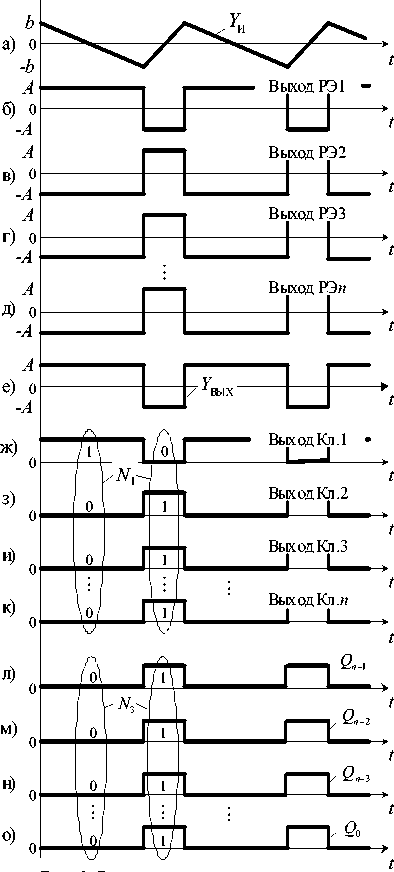
Рис. 3. Временные диаграммы сигналов интегрирующего АЦП – ЦАП при k = 0 и –1,0 <  m < 1,0

рового кода на выходе ЦАП; N 1 – цифровой код на выходе ключей Кл.1 … Кл. n ; N 2 – цифровой код, задаваемый ИК; N 3 – цифровой код на выходе АЦП.

Для АЦП – ЦАП входной сигнал можно представить в виде выражения Х ВХ = ±А ( к + 0,5 m ) , где А = 2 A _max N _max = 2 A - вес единицы младшего разряда преобразуемого кода в аналоговой форме;

i = n — 1

N™х = V 2i = 2n — 1 — максимальное значение max i=0

двоичного цифрового кода в десятичной системе счисления, формируемого на выходе ключей преобразователя Кл.1 ... Кл. n ; А = A m_ax/ N max - амплитуда импульсов на выходе релейных элементов РЭ1 … РЭ n ; А max – максимальная амплитуда сигнала на выходе ЦАП; к = 0,1, 2, ... , ( N max — 1)/2

– целые числа, соответствующие десятичным числам преобразуемого кода; m – коэффициент, учитывающий изменение входного сигнала на интервале А ( — 1,0 <  m <  1,0).

Рассмотрим работу устройства при наличии гистерезиса у релейных элементов РЭ1 … РЭ n и для входного сигнала Х ВХ = 0, когда числа k = 0 и m = 0 (рис. 2).

Будем считать, что релейный элемент РЭ1, формирующий старший разряд преобразуемого кода, находится в «положительном» состоянии (рис. 2, б). Тогда амплитуда на выходе пропорционального звена П1 равна А - 2 ^{n -1}. Для выполнения равенства Х ВХ = Y ВЫХ все остальные РЭ2 … РЭ n в системе вынуждены переключиться в «отрицательное» положение (рис. 2 в – д), когда суммарный сигнал на выходе Σ ВЫХ равен

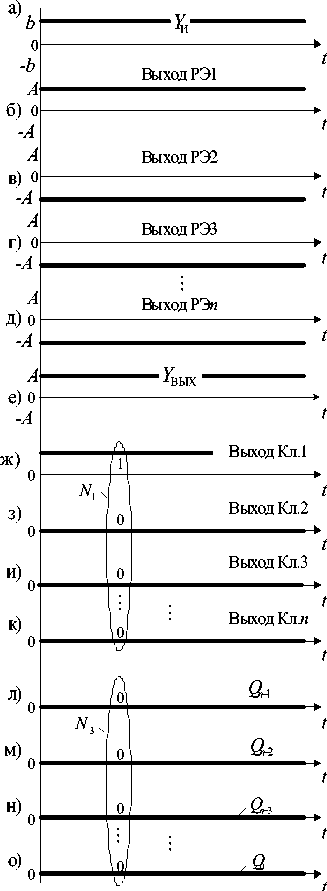
Рис. 4. Временные диаграммы сигналов интегрирующего АЦП – ЦАП при k = 0 и m = 1,0

а)

-b

А

• б)    0 -А

А

• в)    0 -А

А г) 0 -А

А д) 0 -А

Y _И

( N — 1) + b max

A - N

Выход РЭ1

t

Выход РЭ2

t

Выход РЭ3

t

t

Выход РЭ n

Y

ВЫХ

t

е) 0

t max

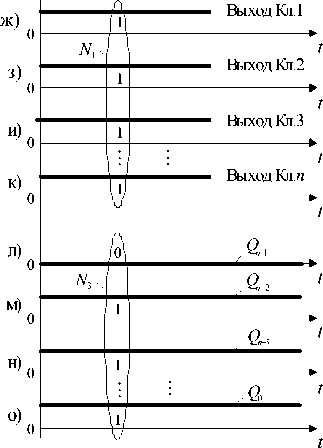
Рис. 5. Временные диаграммы сигналов интегрирующего АЦП – ЦАП при к = ( N _max — 1 )/ 2 и m = 1,0

У вых = А ( 2 n - 1 - 2 n - 2 - 2 n — 3 - ,..., - 2 0 ) = A (рис- 2, е). Условие равенства Х ВХ = Y ВЫХ является невыполнимым для случая Х ВХ = 0, поэтому сигнал Y И на выходе интегратор И начинает линейно спадать под действием напряжения – А с выхода Σ ВХ (рис. 2, а) и при достижение равенства Y _И( t ) = – b первый РЭ1 переключается в «отрицательное» состояние (рис. 2, б), а РЭ2 … РЭ n – в «положительное» (рис. 2, в – д). В результате суммарный сигнал на выходе Σ ВЫХ соответствует значению У вых = А ( - 2 n - 1 + 2 n " 2 + 2 n - 3 - ,..., + 2 0 ) = - A -

Таким образом, при Х ВХ = 0 интегрирующий преобразователь постоянно находится в режиме переключения всех релейных элементов с частотой несущих колебаний f ₀ = 1/ ( 4 bT ) , где b = |b/A | - нормированное значение порогов переключения РЭ1 … РЭ n ; Т – постоянная времени интегрирования интегратора. Величину порогов переключения РЭ1 … РЭ n следует выбирать из условия | b | <  А .

Положительному уровню сигнала на выходе РЭ1 … РЭ n соответствует сигнал логической «1» на выходе ключей Кл.1 … Кл. n , а отрицательному уровню – сигнал логического «0» (рис. 2, б – д, ж – к). В результате при Х ВХ = 0 на выходе ключей Кл.1 … Кл. n формируются два значения двоичного кода N ₁ (рис. 2, ж – к), которые равны: ( N max + 1)/2 и ( N max - 1)/2.

УВК производит операцию поразрядного вычитания из кода N 1 , формируемого на выходе ключей Кл.1 … Кл. n , кода N 2 с выхода ИК так, чтобы цифровой код на выходе преобразователя N 3 = N 1 – N 2 равнялся нулю. Примем значение кода N ₂ = ( N max + 1 ) /2, тогда при Х ВХ = 0 выходной код преобразователя N 3 в десятичной форме будет равен нулю или минус единице (рис. 2, л – о). В результате на выходе АЦП формируется статическая ошибка, равная единице младшего разряда преобразуемого кода N ₃. При большом количестве разрядов интегрирующего преобразователя АЦП – ЦАП ( n >  8) данная ошибка практически не оказывает заметного влияния на точность его работы и ею можно пренебречь.

При других значениях к ^ 0 и m = 0 преобразователь работает аналогично случаю с числами k = 0 и m = 0. При этом в системе обязательно находится в режиме переключения с несущей частотой f о = 1/ ( 4 bT ) хотя бы один из релейных элементов РЭ1 … РЭ n .

Рассмотрим работу преобразователя при других значениях m , отличных от нуля и изменяющихся в диапазоне - 1,0 <  m <  1,0, и к = 0, когда Х _ВХ = ± А m . Для данных значений устройство переходит в режим частотно-широтно-импульсной модуляции (ЧШИМ), при котором частота пере- Серия «Энергетика», выпуск 18

ключения РЭ1 … РЭ n уменьшается в соответствии с выражением f = f ₀ - ( 1 - m ² ) (рис. 3, б - д). Состояние кодов N 1 и N 3 на выходе ключей Кл.1 … Кл. n и выходе преобразователя соответственно (рис. 3, ж – о) сохраняется таким же, как и для случая k = 0 и m = 0 (рис. 2, ж – о).

При m = 1 и любых других целых значениях k частота переключения РЭ1 … РЭ n становится равной нулю и в АЦП возникает установившийся процесс, когда Х ВХ = Y ВЫХ . Например, при Х ВХ = А ( k = 0) релейный элемент РЭ1 переключается в «положительное» состояние (рис. 4, б), а РЭ2 … РЭ n – в «отрицательное» положение (рис. 4, в – д). В результате суммарный сигнал на выходе ЦАП У вых = А ( 2 n ^{- 1} - 2 n ^{- 2} - 2 n ^{- 3} - ,..., - 2⁰ ) = A (рис. 4, е) уравновешивается входным воздействием Х ВХ = А . Напряжение на выходе интегратора И достигает установившегося значения Y И ( t ) = b (рис. 4, а) так, чтобы постоянно удерживать РЭ1 в «положительном» состоянии (рис. 4, б). Цифровой код N 1 на выходе ключей Кл.1…..Кл. n равен значению ( N max ⁺ 1 )/ ² (рис. ⁴, ж – к), а код на выходе преобразователя N ₃ = 0 (рис. 4, л – о).

Аналогичным образом АЦП – ЦАП работает при других значениях k и m = 1. Например, максимально возможному значению к = ( N max - 1 )/2 будет соответствовать максимальный уровень f N^, -1 1) входного сигнала Х _ВХ = ±А I —max-- + 2 1 = ± А N max .

Пусть Х _ВХ = А N max , тогда РЭ1 ^ РЭ n переключаются в «положительное» состояние (рис. 5, б – д).

В результате суммарный сигнал на выходе Е вых , равный У вых = А ( 2 n ^{- 1} + 2 n ^{- 2} + 2 n ^{- 3} + ,..., + 2⁰ ) = = A N max (рис. 5, е), уравновешивается входным воздействием Х _ВХ = А N max . Напряжение на выходе интегратора И достигает установившегося значения У _и ( t ) = ( N _max - 1) + b (рис. 5, а) так, чтобы постоянно удерживать РЭ1 … РЭ n в «положительном» состоянии (рис. 5, б–д). Все ключи Кл.1 … Кл. n находятся в состоянии логической «1» (рис. 5, ж – к), что соответствует максимальному значению кода N ₁ = N _max. При вычитании из кода N ₁ кода N ₂ = ( N _max + 1)/2 на выходе преобразователя получаем код N 3 = ( N max - 1 ) /2 (рис. 5, л - о).

При Х _ВХ = - А N max наоборот все РЭ1 ... РЭ n переключаются в «отрицательное» состояние, когда напряжение на выходе Σ_ВЫХ изменяет знак и становится равным      у _ьк =- А ( 2 n ^{- 1} + 2 n ^{- 2} +

+ 2 n ^{- 3} + ,..., + 2⁰) = - AN™_x . Тогда все ключи ^{, ,}                     max

Кл.1 … Кл. n находятся в состоянии логического «0», что соответствует минимальному коду N 1 = 0.

При вычитании из кода N 1 кода N 2 = ( N max + 1)/2 получаем выходной код N 3 = - ( N max + 1 ) /2 .

Амплитудная N 3 = F ( X ВХ ) и модуляционная f = F ( X ВХ ) характеристики АЦП - ЦАП в относительных единицах приведены на рис. 6, а, б соответственно. Здесь Х _ВХ = | Х _ВХ/ ^ m_ax| - нормированное значение входного сигнала, отнесенного к максимальной амплитуде на выходе преобразователя A max = A • N max ; f = f/f 0 ^- нормированное значение частоты выходных импульсов РЭ1 … РЭ n, отнесенной к несущей частоте f 0 = 1/ ( 4 bT ) при нулевом значении сигнала на входе АЦП.

Рассмотренный интегрирующий АЦП – ЦАП является замкнутой системой, поэтому в установившемся режиме работы уровень сигнала на входе Х _ВХ АЦП преобразователя должен быть всегда уравновешен выходным напряжением Y ВЫХ ЦАП. Это возможно только при соответствующем (нужном) коде, формируемым преобразователем. Когда разрядность ЦАП не обеспечивает нужную точность (дискретность) преобразования между уровнями, то между ними начинается режим частотно-широтно-импульсной модуляции (режим состязаний).

Однако усредненная интегральная точность всегда обеспечивается из-за наличия интегратора в прямом канале регулирования. В результате амплитудная характеристика (рис. 6, а) будет всегда линейной, а на появляющуюся частотно-широтноимпульсную модуляцию между дискретами указывает модуляционная характеристика на рис. 6, б.

Если говорить об известных АЦП, то в них всегда вводилось понятие «тактируемость», которая определяла жесткий порядок работы и иерархию элементов АЦП за цикл преобразования. При этом величина этого «такта» всегда диктовалась наиболее инерционным узлом схемы АЦП («слабым звеном»), который навязывал время этого такта преобразования остальным, в том числе и быстродействующим элементам всего устройства. Этот недостаток характерен для всех импульсных (т. е. тактируемых) систем автоматического управления.

Экспериментальная проверка теоретических положений была проведена на схеме четырехразрядного преобразователя, показанного на рис. 7 (без УВК). Там же указано функциональное назначение элементов принципиальной схемы. Интегратор выполнен на операционном усилителе (ОУ) А1. Сумматоры А4, А5, А8, А11 и инверторы А2, А7, А10 реализованы по традиционным схемам пропорциональных усилителей. Функции релейных элементов выполняют ОУ А3, А6, А9, А12 с положительной обратной связью по напряжению,

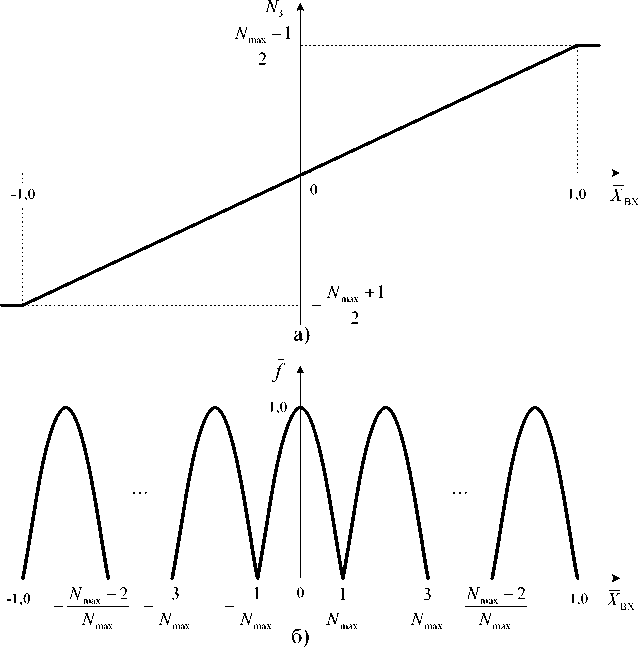
Рис. 6. Амплитудная (а) и модуляционная (б) характеристики интегрирующего АЦП – ЦАП с бестактовым поразрядным уравновешиванием

обеспечивающей неинвертирующую петлю гистерезиса и симметричные относительно «нуля» пороги переключения.

Осциллограммы на рис. 8, а соответствуют случаю нулевого значения входного сигнала. При гармоническом входном воздействии (рис. 8, б) выходной сигнал ЦАП имеет форму ступенчато-аппроксимированной синусоиды. Искажения формы «ступенек» и «дребезг» фронтов вызваны свойствами цифрового осциллографа.

Статическая температурная и временная погрешность АЦП – ЦАП соответствует паспортным данным операционных усилителей, работающих в режиме интегратора АЦП и выходного сумматора ЦАП.

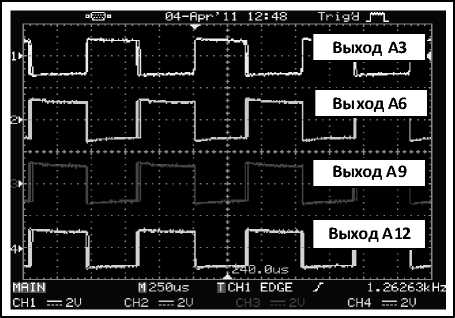
На рис. 9 приведены экспериментальные логарифмические частотные характеристики АЦП – ЦАП, которые показали, что полоса равномерного пропускания частот зависит только от постоянной времени Т интегратора И.

В тех случаях, когда приоритетным фактором является быстродействие целесообразно использовать разомкнутую структуру АЦП – ЦАП, фрагмент которой приведен на рис. 10, а. Здесь интегратор заменен буферным усилителем Ус. Там же на рис. 10, б, в приведены временные диаграммы

10K

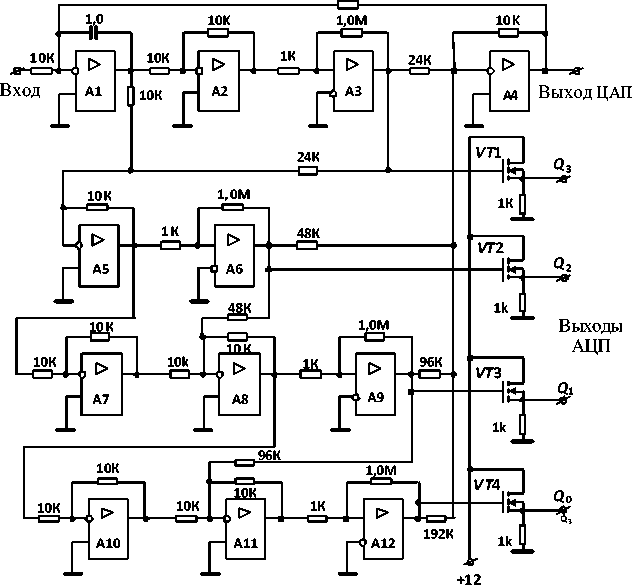
Рис. 7. Фрагмент принципиальной электрической схемы четырехразрядного интегрирующего АЦП – ЦАП с бес-тактовым поразрядным уравновешиванием (А1 – интегратор; А4, А5, А8, А11 – сумматоры; А2, А7, А10 – инверторы; А3, А6, А9, А12 – релейные элементы; VT 1 – VT 4 – ключи IRFD 014; (А1 … А12 – LM 6171))

а)

Рис. 8. Осциллограммы сигналов четырехразрядного интегрирующего АЦП – ЦАП с бестактовым поразрядным уравновешиванием

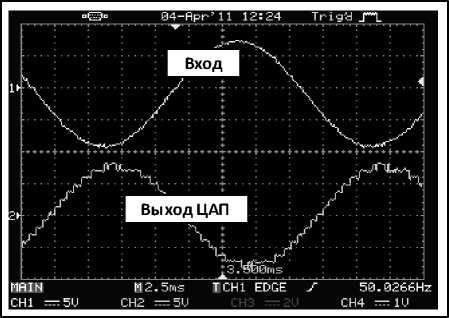
б)

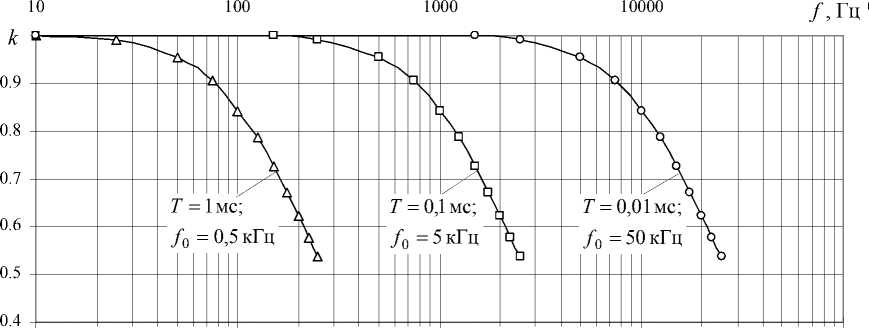
Рис. 9. Логарифмические амплитудно-частотные характеристики интегрирующего АЦП – ЦАП с бестактовым поразрядным уравновешиванием

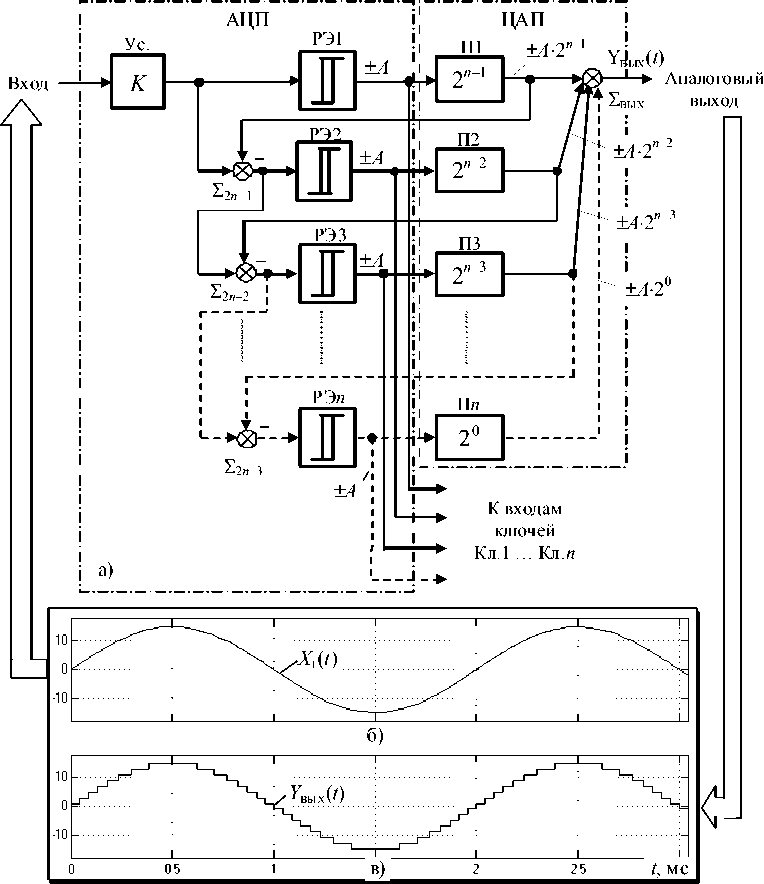
Рис. 10. Фрагмент структурной схемы скоростного АЦП – ЦАП с бестактовым поразрядным уравновешиванием (а) и временные диаграммы его сигналов (б, в) при частоте входного гармонического воздействия 500 Гц сигналов «вход- выход» при гармоническом входном воздействии для n = 4, полученные в результате моделирования АЦП – ЦАП в среде MatLab + Simulink.

Моделирование проводилось при следующих параметрах: максимальная амплитуда на выходе ЦАП А max = 15 В, вес единицы младшего разряда преобразуемого кода в аналоговой форме A = 2 А _max/(2 n -1) = 2 В, амплитуда импульсов на выходе релейных элементов РЭ1 … РЭ4 А = А max /(2 ⁿ – 1) = 1 В, нормированные значения порогов переключения релейных элементов РЭ1 РЭ4 b = \Ь[А\ = 0,05.

В данном случае полоса пропускания АЦП – ЦАП ограничивается лишь динамическими возможностями входящих в него элементов.

Выводы

• 1.    Рассмотренный АЦП – ЦАП относится к классу бестактовых замкнутых интегрирующих систем, обеспечивающих повышенную точность, быстродействие, надежность и помехоустойчивость процесса преобразования входного сигнала.

• 2.    Применение интегратора позволяет обеспечить высокую помехоустойчивость, надежность устройства, а бестактовое поразрядное управление – высокое быстродействие по сравнению с интегрирующими АЦП.

• 3.    Температурная и временная стабильность характеристик АЦП – ЦАП всецело определяется дрейфовыми параметрами операционных усилителей интегратора АЦП и выходного сумматора ЦАП. Полоса пропускания АЦП – ЦАП зависит только от постоянной времени канала интегрирования.

• 4.    Значительное расширение полосы пропускания АЦП – ЦАП возможно в его разомкнутой структуре при отсутствии канала интегрирования.

• 5.    Несмотря на целый ряд существенных преимуществ рассмотренного метода АЦП – ЦАП, необходимо отдавать себе отчет в том, что его дальнейшая судьба во многом будет определяться позицией фирм-производителей интегральных микросхем и их заинтересованностью в расширении устоявшейся номенклатуры своих изделий.

Здесь быстродействие будет зависеть только от динамических возможностей элементной базы АЦП – ЦАП. Однако при этом существенно снизиться помехоустойчивость устройства.