О новых решениях уравнений пластичности, полученных с помощью высших симметрий

Основным свойством симметрий, допускаемым системой дифференциальных уравнений, является то, что под их действием любое решение системы уравнений переходит в решение этой же системы. Это свойство позволяет получать новые решения не интегрированием исходной системы, а применением групповых преобразований к уже известным решени- ям. Таким способом найдены многие интересные решения для различных дифференциальных уравнений. В данной статье представлено, как можно использовать высшие симметрии для построения точных решений из решения Прандтля.

Рассмотрим дифференциальные уравнения теории идеальной пластичности в плоском случае [1]:

3g          3939

F1 =--2 k (cos 29—+ sin 29 —) = 0, дx           дx

F2 =--2 k (sin 29--cos 29 —) = 0, дy           —x—

где g,=g-ksin29, g =g + ksin29, t = kcos29 -xy компоненты тензора напряжений; ст - гидростатиче- п ское давление; 9 = (1; x) -—,(1; x) - угол между первым главным направлением тензора напряжений и осью OX.

Известно, что система уравнений (1) допускает бесконечную группу точечных симметрий, бесконечную алгебру высших симметрий и бесконечную систему законов сохранения [2].

Точечная группа, допускаемая системой (1), уже неплохо изучена. С ее помощью удалось построить новые серии точных решений уравнений (1) и изучить качественные свойства этих уравнений.

Законы сохранения, допускаемые системой (1), позволили решить краевые задачи Коши и Римана в аналитическом виде.

В данной статье впервые будет показано, как высшие симметрии могут быть использованы для построения новых точных решений уравнений (1).

Приведем необходимые сведения о высших симметриях уравнения (1).

Пусть д+G = 1 дxi дyj j

д ‘^{+ j} 9 д x i д y^j

= p j , i , ^j = 1, ²,....

Рассмотрим бесконечномерное пространство J” с координатами (x, y, ст, 9, pkk), k = 1, 2,..., и преобра- зование этого пространства вида x ' = f 1( x, y, g, 9, pk, a), y ' = f2(x, y,G,9, Pk,a), g' = g 1( x, y, g, 9, pk, a),                 (2)

9' = g 2 ( x , y , g , 9 , p^k , a ),

(pk)' = hk (x,y, g, 9, pk, a), k = 1,2,..., i, j = 1,2,..., где α – одномерный параметр из некоторой окрестности нуля.

Пусть преобразования (2) составляют локальную однопараметрическую группу. Тогда д'+ jG    , (p2 )        — ^ ",....

д ( x ) i д ( y ) ^{j   j}         д ( x )¹ д ( y ) ^j

Система уравнений (1) определяет в пространстве J ^∞ бесконечную систему уравнений

D _v ( F ) = 0, D _v ( F 2 ) = 0.

Здесь оператор полной производной имеет вид

д k д

D = ⁺ A ^pM,j - к , ^д x k л j , j д pk j

д k д

Dy = + A p‘, j+1 a k , дy   k,-,j         дp-,j v = (l, m), Dv= Dx% Dym, где v - любое целое число.

Будем говорить, что система уравнений (1) допускает группу преобразований (2), если бесконечная система (3) инвариантна при этих преобразованиях.

Каждой однопараметрической группе (2) соответ-

Гф1)

ствует производящая функция симметрий ф = I   I ,

1^2 )

которая определяется по системе уравнений iFФ = 0,                         (4)

где черта вверху означает, что в уравнениях (4) следует перейти на многообразие (1).

Оператор lF из (4) для системы (1) будет следую щим:

(               39         39 )

D.    - 2k(-2sin29—- + 2cos29 —+

x

дx         дy

+ cos 2 9 D_y + sin 2 9 D., )

=                                                 .

Dv - 2k(2cos29 — + 2sin29 д9 +

y             дx         дy

+ sin 2 9 D_y - cos 2 9 D. .)

V x y 1               7

Подробности вычислений высших симметрий и многочисленные примеры можно найти в [2] и цити- руемых там источниках.

В [2] найдены все высшие симметрии, допускаемые уравнением пластичности (1). Простейшие из них имеют вид

f 2 =	Г— 2 y ' д^ 2 д 2 y	, f 3 =	■ . ' д^ 3 д 3 y	,..., f n =	n 5Z —^ n д ny	,.... (5)
	V—n 2 )		V—n 3 )		V—n n )

Используем некоторые эти симметрии для построения новых решений пластичности согласно следующей методике.

Пусть x0, y0 – некоторые известные решения уравнений пластичности, а fk возьмем из семейства симметрий (5).

Серия новых решений, которые получаются из точного решения x 0 ( ^ , n ), y 0 ( ^ , n ), определяется как решение системы уравнений

Sy = д ky 5x = д ky дт д^k , дт —п k

со следующими начальными условиями:

y (0,^,n) = y0, x (0,^,n) = x0.

Тогда пара функций ( y ( т , ^ , n ) , x ( т , ^ , n ) ) является решением уравнений пластичности для каждого т .

Единственное затруднение при использовании этой методики состоит в отсутствии формул для решения задачи Коши для уравнений (6), которых нет, например, даже в [3].

По аналогии со случаем к = 2 запишем общее решение уравнений (6).

Лемма. Решение задачи Коши

3y = 5 ky _

дт 5Чк , У

| = 0 = у 0 можно представить в виде

« т i d (ik) У у(т,Ч,Ч) = У0 + £--—(к0. (7)

i = 1 ¹ ! d ^Ч

Доказательство этой леммы осуществляется простой проверкой того, что (7) действительно есть решение уравнения (7) и удовлетворяет начальному условию.

В качестве исходного решения возьмем решение Прандтля:

x0 (Ч,n) = -sin6-(п + Ч)cos6,у0 (Ч, n) = cos 6 + (п + Ч) sin 6.

x = ( 2 6- sin 2 6 + c 1 ) ch a - cos 2 6 sh a , у = cos 2 6 ch a - ( - 2 6- sin 2 6 + c 1 ) sh a .

Графики новых точных решений уравнений пластичности при а = 0, а = 1, а = 2 и а = 3 представлены ниже (рис. 1–4).

Подставляя это решение в (7) и сворачивая полученные ряды, имеем

x (т,Ч,n) = (-sin6-(п + Ч)cos6 + тsin6)expу (т, Ч, n) = (cos 6 + (n + Ч) sin 6 + т cos 6) exp

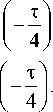
Характеристики для этого решения и решения На-даи приведены в [4].

Теперь, используя решение Прандтля, рассмотрим случай к = 3. Согласно предыдущим рассуждениям

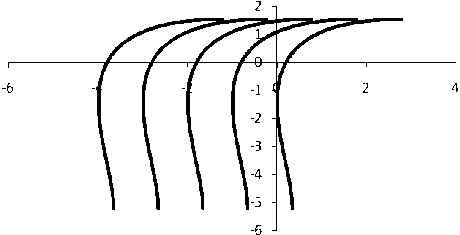
Рис. 2. Линии скольжения первого семейства нового решения при a = 1

получим

x (т, Ч, n) = (-(п + Ч) cos 6

+

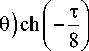
+ ((n + Ч)sin6-cos 6)shI -- I, к 8 J

У (т, Ч, n) = ((п + Ч) sin 6

+

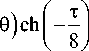
((n + Ч) cos 6

- sin 6 ) sh

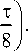
Возвращаясь к исходным координатам, по формулам x = x cos 6 - у sin 6 , у = x sin 6 - у cos 6 имеем

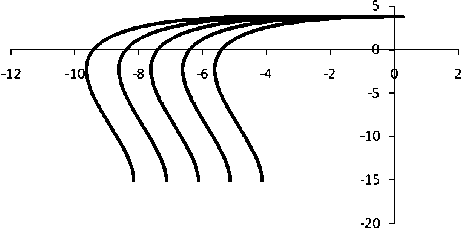
Рис. 3. Линии скольжения первого семейства нового решения при a = 2

x = (-a- sin 26) ch a - cos 26 sh a, у = cos26 ch a + (a-sin 26) sh a, f т где a = - к 8

Характеристики и соотношения на характеристиках для этого решения имеют вид

Ч = a - 26 = c1,

x = ( - 2 6- sin 2 6- c 1 ) ch a - cos 2 6 sh a , у = cos 2 6 ch a - ( 2 6- sin 2 6 + c 1 ) sh a , n = a + 2 6 = c 1 ,

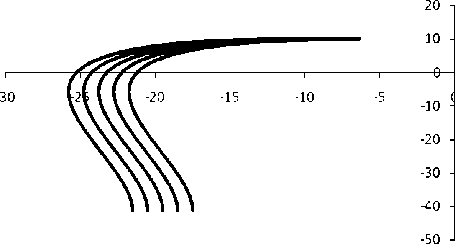
Рис. 4. Линии скольжения первого семейства нового решения при a = 3

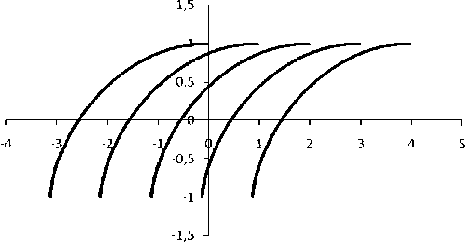
Рис. 1. Линии скольжения первого семейства решения Прандтля - нового решения при a = 0