О параболической аппроксимации температурного поля слябов при нагреве в методических печах

Известно, что еще в 50-х годах прошлого столетия М.А. Био предложил мгновенное распределение температуры по пространственным координатам в массивном теле представлять с помощью параболы [1]. Привлекательность такого подхода объясняется тем, что параболу можно однозначно характеризовать «…небольшим числом параметров…» [2, с. 352], что значимо упрощает описание температурного поля и весьма существенно уменьшает необходимый для его хранения объем памяти компьютера. С этой же целью – с целью сокращения необходимого объема памяти компьютера – в работе [3] применялась аппроксимация температурного поля слябов при нагреве в методических печах многочленами второго и четвертого порядков по координате х - толщине нагреваемой заготовки. Для этого начало координат выбиралось в точке с нулевым тепловым потоком, что и позволяло исключить в аппроксимирующем многочлене наличие нечетных степеней координаты х и тем самым уменьшить количество подлежащих определению его коэффициентов.

Обоснованность такого подхода аргументируется также и тем, что, как это указано в работе [4, с. 157], «…из решений уравнения теплопроводности … известно, что при постоянной скорости нагрева и постоянном тепловом потоке с наступлением так называемого регулярного режима распределение температур по сечению пластины подчиняется параболическому закону». Здесь вполне уместно заметить, что, как это отмечено в работе [5, с. 159], «…многолетний опыт работы различных научно-исследовательских учреждений показывает, что метод регулярного режима является эффективным средством решения инженерных задач».

К месту также заметим, что о наличии параболической составляющей в решении задачи нагрева пластины в печах в свое время указывал еще Г.П. Иванцов в работе [6, с. 59–60].

Известны также и другие работы, в которых температурные поля в телах достаточно успешно аппроксимируются степенными многочленами не выше 3-го порядка [7–9].

Постановка задачи

Таким образом, метод парабол достаточно привлекателен при решении задачи расчетного контроля температуры нагреваемых заготовок в системах управления, работающих в режиме реального времени. Поэтому существенно важными являются вопросы о том, как конкретно в этом случае следует вычислять параметры аппроксимирующей параболы, насколько предлагаемое описание температурного поля соответствует общеизвестному математическому представлению процесса, в какой мере оно приемлемо, в том числе и для целей использования в составе математического обеспечения автоматизированных систем управления технологическими процессами (АСУ ТП). Поэтому далее рассмотрим особенности применения этого метода.

Общее решение задачи

Как это хорошо известно [10–15], нагрев слябов в методических печах можно представить с помощью математической модели следующей структуры:

dt(x,T) д A dt(x,T)\ л         г/п бт> д- д, Р д, b00- (1) t(x, 0) = t0(x), 0 < х < L;(2)

д^= 0,т> 0;(3)

дх

Ад^ = а[£п(т) — £(^т)],т>0.(4)

Здесь с т , р и Л - соответственно теплоемкость единицы массы, плотность и коэффициент теплопроводности, зависящие в общем случае от температуры С(х,т); х - пространственная координата; т - время; L - расчетное сечение заготовки; t⁰(x) - заданная функция, описывающая начальное температурное поле металла; а - коэффициент теплоотдачи; С _п (т) - температура рабочего пространства печи.

Предположим, что нестационарное температурное поле слябов удовлетворительно описывается следующей параболой:

С(х,т) = а(т) + Ь(т)х + с(т)х².                                                         (5)

Здесь а(т), Ь(т), с(т) - параметры (коэффициенты) параболы, которые подлежат определению в процессе решения задачи моделирования.

Рассмотрим один из вариантов определения этих коэффициентов. Для этого подчиним непосредственно соотношение (5) уравнениям модели (1)–(4), тогда будем иметь:

стР [^dT + х ТО7 + х2 ^7)] = Л • 2с(т), 0 < х < L, т > 0;(6)

а(0) + й(0)х + с(0)х2 = С0(х), 0 < х < L;(7)

й(т) = 0,т>0;(8)

Л[Ь(т) + 2c(t)L] = а[сп(т) — а(т) — b(r)L — c(t)L2],t > 0.(9)

стР Кт + х2 TFT] =Л•2с(т),0 0;(10)

а(0) + с(0)х2 = С0(х), 0 < х < L;(11)

A2c(t)L = а[сп(т) — а(т) — c(t)L2],t > 0.(12)

При этом из соотношения (12) следует, что а(т) = tnCO — (^ + L2) с(т).(13)

Поэтому, подставив данное выражение в (10), получим следующее обыкновенное линейное дифференциальное уравнение относительно с(т):

М^+[х2 — (V+L2)]a7W^(T)-04)

или

Т + ^ / [(“ + L2) — х2] с(т) = 1/ [(^ + L2) — х2] \.

Известно [16], что общее решение данного уравнения может быть представлено в следующем виде:

^с(т) = [(2И/«+Ч)_х " | Т ^exp {](^^7i;y5]'®^-т)}^_л^_d^ ⁺

+consrexp {-J^-l1).

Поэтому для коэффициента а(т) можно записать

^а(т) = t n ft)^— (— ^{+ l 2 )} { |(^_m2)_,₂| ^ ^exp { [(S tJ' )-^] к ^{— т)})^т⁴5⁺

X ,  ( ST)

+const• exp — _г,д, ^т\ —_гт к K“«^-R]

Таким образом, с помощью соотношений (16) и (17) можно определить искомые числовые значения коэффициентов параболы для любого закона изменения температуры печи во времени.

Анализ и конкретизация решения для случая постоянной температуры печи

При постоянной во времени температуре печи tn (т) = tnn получаем, что с(т) = const •exp {-йй^^т}, тогда

а(т) = tnn — (— + L2) const • exp {—   W^.p)— т}.(19)

у J пп к а /             ' I [(2XL/a+L2)-x2] J

Из данных формул следует, что lim _T ^ _ra с(т) = 0, а lim _T ^ _ra а(т) = t _nn , это вполне согласуется с физическими представлениями о процессе нагрева.

Из вышеприведенных уравнений следует, что числовые значения коэффициентов параболы зависят не только от времени, но и от координаты %, следовательно, в действительности распределение температуры по толщине заготовки более сложное, чем парабола. Поэтому необходимо признать, что кусочно-полиномиальная аппроксимация температурного поля, используемая в работах [7–9], является более точной. К месту заметим, что в работе [6, с. 59] отмечено следующее: «.. .общее решение уравнения Фурье представляет собой полином степени и».

Как это следует из вышеприведенных формул, для дальнейшей конкретизации решения задачи необходимо как-то, исходя из начального условия, определять числовое значение const. При этом следует иметь в виду, что само решение задачи предполагает только параболическое начальное распределение температуры, что не всегда соответствует действительности. Таким образом, самим подходом к решению задачи моделирования закладывается ошибка в аппроксимации реального начального температурного поля. Однако и такой подход может быть оправдан тем, что с увеличением времени процесса, с наступлением так называемого регулярного режима нагрева влияние начального температурного поля заметно ослабевает [5]. Более того, «…теория регулярного режима позволяет в некоторых случаях проводить приближённые расчёты нестационарных температурных полей … когда принимается, что температурное поле тела или системы тел входит в стадию регулярного режима с самого начала рассматриваемого процесса» [5, с. 149].

Из уравнений (18) и (19) следует, что расчетное начальное температурное поле С ° (х) будет иметь вид:

^£ р (%) = t _nn — ( "О- + L²) const + const • %².                                                (20)

Вполне понятно, что в общем случае оно не может быть равно реальному распределению температуры в заготовке в начале нагрева t p (%) ^ t⁰(%), т. е. соотношение (11) при таком подходе может быть выполнено только приближенно. Поэтому для определения const воспользуемся таким понятием, как «важнейшие температуры в теле» [17], а именно понятием «среднемассовая температура», и будем считать, что в начале нагрева должны быть равны только средемассовые температуры (расчетная t 0 и реальная t⁰). Исходя из этого, получаем следующее уравнение для определения константы:

f _— f O ^const = 277—2-a V²

.

Поэтому конкретное выражение для начального температурного поля при данном подходе к моделированию процесса нагрева будет иметь вид:

^t p ⁽%^{)    t} 77

— (V+L2>

^f 77 ^{f O} ^₊ 2 _L 2 a з

+

^f nn ^{f O}     2

^+2 - 2 % .

a з

Заметим, что при таком подходе, каким бы ни было реальное начальное распределение температуры в заготовке, расчетное распределение всегда будет именно таким, как это указано в формуле (22).

Таким образом, при рассматриваемом подходе к моделированию нестационарное температурное поле заготовки при постоянной температуре печи будет описываться следующим доста- точно простым уравнением:

t(%,т) = tnn + J^ • exp |— ^рЧ-д—р"^ ’ (%2 - V - L2).

Как это нетрудно заметить из (23), данный метод привлекателен не только по причине небольшого числа характеризующих параболу параметров, но и по причине простоты получающегося математического описания температурного поля (небольшого объема вычислительной работы), что достаточно важно для задачи расчетного контроля температуры нагреваемых заготовок.

Вычислительные эксперименты

На рис. 1 представлены результаты расчета по данному соотношению (методу парабол) температурного поля заготовки для некоторых моментов времени при t _nn = 1300 ⁰C; ^ = 0,02 мч ² ; L = 0,1 м;

A = 40,705   ; a = 407,05    ; t ° = 20 C.

, мС         ,    m²C

На рис. 2–4 приведены кривые распределения температуры в заготовке, вычисленные по методу парабол и по классическому (точному) методу Фурье для случая равномерного начального температурного поля в 20 С и соответственно для моментов времени т = 0,5 ч, т = 1,0 ч и т = 1,5 ч. Здесь к месту необходимо подчеркнуть, что рассматривается наиболее неблагоприятный для данного подхода случай – случай равномерного на- чального распределения температуры. Здесь во всех случаях звездочками помечены кривые, рассчитанные по методу парабол.

Как видно из рис. 2–4, наибольшее различие температур наблюдается для центра (% = 0) и поверхности заготовки (% = L), причем это различие уменьшается с увеличением времени нагрева. Поэтому можно заключить, что рассматриваемый подход к описанию процесса нагрева становится более точным по мере приближения регулярного режима нагрева. При этом, однако, следует иметь в виду, что «…время регуляризации температурного поля в теле зависит … и от начального распределения температур» [5, с. 155]. Отсюда следует заключить, что чем ближе начальное распределение температуры будет к заложенному в предлагаемом методе, тем выше будет точность расчета уже с самых начальных моментов времени.

Многочисленные расчеты также показали, что различие среднемассовых температур, вычисленных по точному методу Фурье и по методу парабол, практически не существенно. Так, например, для случая на рис. 2 среднемассовая температура, вычисленная по методу парабол, составляет 695,5 °C, а по точному методу Фурье - 698,9 °C. Впрочем, несущественность

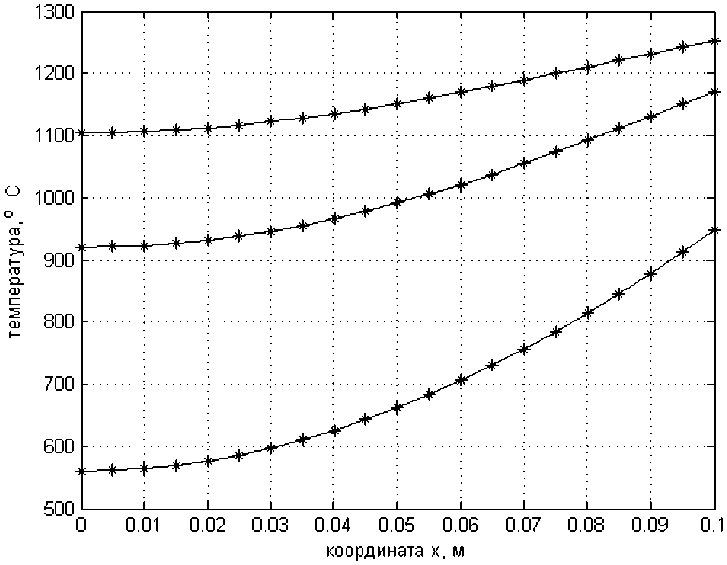
Рис. 1. Распределение температуры в заготовке: нижняя кривая - при т = 0,5 ч; средняя - при т = 1, О ч; верхняя - при при т = 1,5 ч Fig. 1. Temperature distribution in the workpiece: lower curve at т = 0,5 h; middle - at т = 1,0 h; upper - at т = 1,5 h

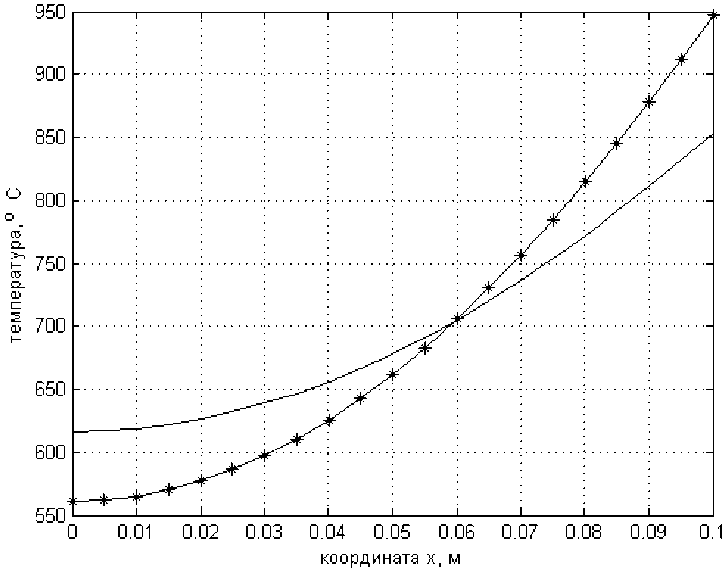
Рис. 2. Кривые распределения температуры в заготовке, вычисленные по методу парабол и по классическому методу Фурье для момента времени т = 0,5 ч

Fig. 2. Temperature distribution curves in the workpiece, calculated using the parabola method and the classical Fourier method for the time moment т = 0,5 h

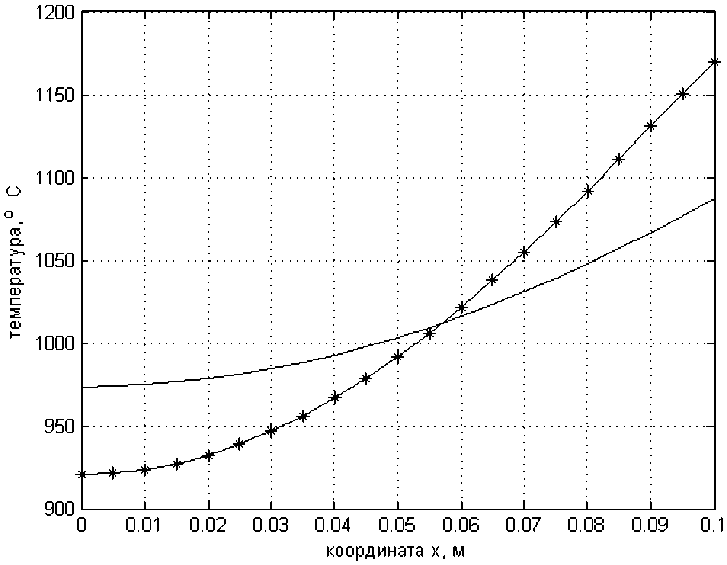
Рис. 3. Кривые распределения температуры в заготовке, вычисленные по методу парабол и по классическому методу Фурье для момента времени т = 1, О ч

Fig. 3. Temperature distribution curves in the workpiece, calculated using the parabola method and the classical Fourier method for the time moment т = 1,0 h

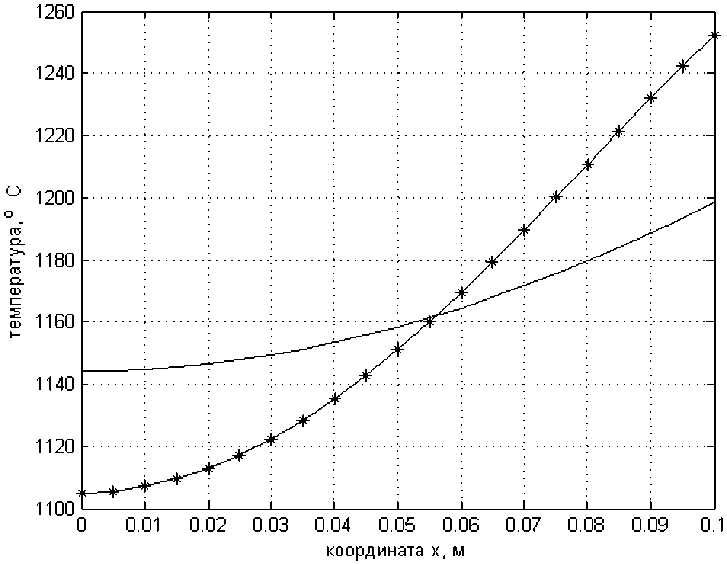
Рис. 4. Кривые распределения температуры в заготовке, вычисленные по методу парабол и по классическому методу Фурье для момента времени т = 1,5 ч

Fig. 4. Temperature distribution curves in the workpiece, calculated using the parabola method and the classical Fourier method for the time moment т = 1,5 h

различия расчетов среднемассовой температуры можно проследить и визуально по графикам рис. 2–4: площади под кривыми точного и приближенного распределений температур по сечению сляба практически одинаковы. Поэтому метод парабол без каких-либо опасений может рассматриваться как простой и достаточно точный метод расчета среднемассовой температуры слябов, причем зачастую и с самого начала процесса нагрева. Это значимо, так как для качественной прокатки металла, в первую очередь, важно общее теплосодержание заготовки, выдаваемой из печи. Если при этом учесть, что с увеличением времени нагрева заметно уменьшается и погрешность вычисления других температур заготовки, то метод парабол вполне можно рекомендовать для использования в составе матема- тического обеспечения систем управления, работающих в режиме реального времени.

Выводы

Метод парабол, несмотря на простоту математического представления, позволяет практически без погрешности вычислять среднемассовую температуру слябов и может быть применен для приближенного описания процесса нагрева при разработке и реализации АСУ ТП методических печей. При этом следует отметить, что погрешность расчета профиля температур по сечению заготовки имеется и зависит от того, насколько начальное распределение температуры по сечению сляба отличается от параболического, эта погрешность заметно уменьшается к концу процесса нагрева.