О перераспределении напряжений в ортотропной вязкоупругой пластинке в окрестности круглого включения

Рассматривается задача о растяжении постоянными распределёнными силами ортотропной пластинки с круглым включением радиусом R . Включение расположено в центре пластинки, растягивающие силы направлены вдоль одного из направлений симметрии вязкоупругих свойств (рис. 1) или под углом 45 ° . Возможны три вида включений: 1) отверстие (включение отсутствует); 2) абсолютно жёсткое включение; 3) упругое включение.

Пусть материал пластинки занимает в пространстве область V II , а включение область V I . Тогда постановка соответствующей задачи теории упругости в случае отсутствия включения и для абсолютно жёсткого включения имеет вид:

уравнения равновесия

"l x ( x ^, y ) ⁺ ( x ^, у ) ^{= 0,} -o ?( x ^, y ) ⁺ ( x ^, у ) ^{= 0,} ( x ^, y ) ^е V I ;⁽¹⁾

геометрические соотношения

8 xx ( x, у )=^X ( x, у ), 8 уу ( x, у )="ЦТ ( x, у ),

Yxy (x,у) = "ux(x,у) + —^(x,у),(x,у) е VIZ; oy        ox

Y

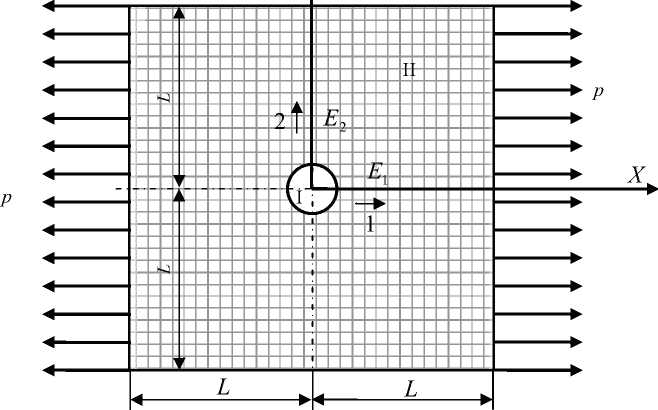
Рис. 1. Схема нагружения пластинки: I - материал включения; II - материал пластинки физические соотношения в условиях плоского напряжённого состояния (ПНС) пластинки

£ xx ( x, У ) =    (° xx ( x, У )-V1° yy ( x, У )) , £ yy ( x, У ) =

E

1             ¹                                          1                                (3)

= —( ° yy ( x , y ) ^-v 2 ° _xx ( x , y ) ) , y xy ( ^x , y ) = -^т xy ( x , y ) , ( x , y ) - V ⁿ;

E 2                               G граничные условия

°       = p , т = 0, °       = т = 0,

^xx l x =± L          ^xy l x =± L          ^yy\y =± L     ^xy\y =± L

• -    пластинка с круговым отверстием, не содержащим включений

(°уул. +т ,п           = 0, (т,упу +о, n           = 0;

V xx ^{x xy y} x ² + y ² = R ²        V ^{yx x yy y} x ² + y ² = R ²

• -    пластинка с круговым отверстием, содержащим жёсткое включение

“ 4 . 2 . , 2 . R 2 = °> " y L2 . y 2 . R 2 ⁼ ^

Для случая упругого включения на его границе должно выполняться условие и1          = м11         , и1          = Мп х1х 2 + у 2 = R 2      х1х 2 + у 2 = R 2, у1х 2 + у 2 = R 2      у1х 2 + у 2 = R 2, где и1 - перемещения в материале включения, и11 - в материале пластинки. Кроме того, уравнения равновесия (1) и геометрические соотношения (2) записываются для (х, у)е V, где V = V1 и V11, а физические соотношения (3) дополняются уравнениями

£ хх ( х, у )=    (п хх ( х, у )-V1C уу ( х, У )) ,е уу ( х, У ) =

E 1

=    ( ^п уу ( ^х ’ у ) ”^V 2 ^g хх ( ^х , у ) ) , У ху ( ^х , у ) = “^т ху ( ^х , у ) , ( ^х , у ) ^е V •

E 2                                G

Предполагается, что модули упругости включения в 2 раза меньше, чем пластинки, а также R <<  L .

При постановке задачи в рамках теории линейной вязкоупругости физические соотношения (3) примут вид

^ хх  П ххСхх + П ху Суу ’ ^ уу  П ху Схх + П уу Суу , у ху  П хуху ^ху ,

*        *        **

где П _хх , П _уу , П _ху , П _хуху - интегральные операторы вида

(         tr)

Пхх)'(I)= /пхх(t-т)df (т) = Пхх(0) f (t)+ f«„(t-т)f (т)dг 0                            10

t                                              У

^П ’ >у / ( t ) = ! ^П уу ( t -т ) df ( т ) = ^П уу ( ⁰ ) f ( t ) + J K„ ( t -т ) f ( т ) d т

0                                I        0

t                                              У

Пху/(t)=фху(t-т)df(т) = Пху(0) f(t)+ Jk,,(t-т)f(т)dт 0                            10

t

П Lvf (t )= П   (t -т) df (т) = П

xyxy             xyxy                     xyxy

У t

(0) f (tMкхуху (t -т) f (т) dт .

V 0

Как видно из постановки, задача является многооператорной и её решение традиционными методами, ориентированными на наличие в структуре решения одного оператора, невозможно, поэтому зачастую прибегают к некоторым упрощениям в самой постановке.

Из многолетней практики решения подобных многооператорных задач сложился ряд упрощающих гипотез. В их числе гипотезы: 1) вязкоупругие свойства проявляются только при сдвиге [1, 2, 3]; 2) ядра всех операторов могут быть выражены через одну функцию времени [4, 5]. Эти гипотезы приводят к изменению самой постановки задачи, однако позволяют перейти от задачи с несколькими операторами к задаче с одним оператором, что значительно упрощает процесс решения.

Решим рассмотренную задачу с применением каждой из гипотез, а также в общей многооператорной постановке.

Для описания вязкоупругих свойств пластинки воспользуемся работой [6], в которой приводятся данные об аппроксимации кривых ползучести для некоторых однонаправленных композиционных материалов. Ап проксимация кривых ползучести производилась выражением

£ 1 t )=

Г          -              ,1 I k + J K k ( t -т ) d Т ° kl .                 (6) _          0                        _

Функции ядер K ijk ( t ) = ф m приняты в виде суммы экспонент:

X з

Ф m ( t ) = -f E P im exP ( -P im t ) ,                    ⁽⁷⁾

³ i = 1

где индекс m отвечает за номер ядра ползучести: K 1111 = ф 1 , K 2222 = ф ₂, ^K 1122 = ^ф 3 , K 1212 = ^ф 4 •

В табл. 1. приведены значения параметров функции (7), взятые из работы [6] для однонаправленного стеклопластика.

Таблица 1

Реологические характеристики однонаправленного стеклопластика

Ф 1 ( t )			Ф 2 ( t )			Ф з ( t )			Ф 4 ( t )
I 1111 • 104	X 1 • 104	P 1 i • 104	I 2222 • 10 3	X 2 • 104	P 2 i • 104	I 1122 • 104	X 3 • 104	p 3 i • 104	27 2 I 1212 • 103	X 4 • 103	P 4i • 104
2,02	0	1	1,16	1,87	0,29	0,68	0	1	1,98	4,80	0,28
		1			1,33			1			1,29
		1			3,73			1			3,37

Примечание. В таблице приняты измерения: / ik , X m - мм²/кгс, P mi- - 1/ч.

Также в работе [6] приводятся данные по аппроксимации всех ядер ползучести одной функцией. При этом аппроксимация кривых ползучести (6) записывается следующим выражением:

⁸ » ( t ) = [ I jjkl ^{+ X} m ^Г ( t ) ] ^G kl , где нормированная функция времени Г ( t ) имеет вид

Г( t )- т Я1 - exp (-₽/)]; 0 <Г( t )< 1.             (8)

³ i - I

В табл. 2. приведены значения параметров функции (7).

Таблица 2

Реологические характеристики функции (7)

Р 1 , -10 4 , 1/ч	X 1 - 10 4 , мм2/кгс	X 2 - 10 3 , мм2/кгс	X 3 - 10 4 , мм2/кгс	X 4 - 10 3 , мм2/кгс
0,35	0	1,83	0	4,63
1,25
3,99

Среднеквадратичная относительная погрешность аппроксимации всех ядер ползучести одной функцией (8) для рассмотренного однонаправленного стеклопластика составляет 1,2 % [6].

Для получения вязкоупругих свойств ортотропной пластинки с включениями будем считать, что пластинка состоит из слоёв однонаправленного стеклопластика, чьи свойства нам известны и приведены выше. Слои чередуются: один слой с направлением армирования вдоль направления оси X , второй с направлением армирования вдоль направления оси Y (см. рис. 1). При таком расположении получаем пакет, который можно рассматривать как ортогонально армированный материал. Зная вязкоупругие характеристики однонаправленного стеклопластика, известным образом можно получить характеристики ортогонально армированного стеклопластика.

Задачу о растяжении ортотропной вязкоупругой пластинки с включением будем решать по методу квазиконстантных операторов. Упругую задачу на каждом моменте времени будем решать методом конечных элементов. Используются треугольные элементы с линейной аппроксимацией. Дискретизация составляет 25 элементов на четверть кромки включения. Результаты решения упругой задачи были сопоставлены с известным аналитическим решением, полученным в [7]. Относительная погрешность численного решения не превышает 3 %.

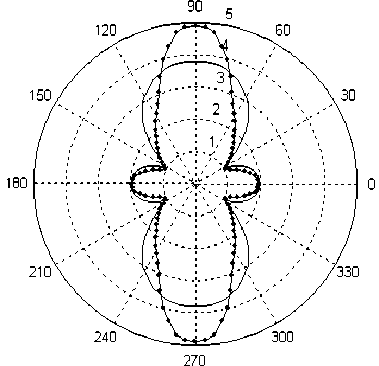
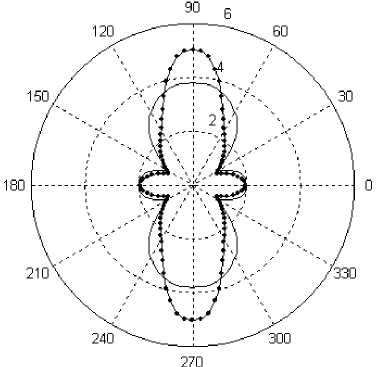
Приведем некоторые результаты решения поставленной задачи. Все изображенные ниже эпюры, по аналогии с [7], взяты по модулю с добавлением 1, что позволяет создать эффект круглого включения с радиусом 1. На эпюрах отображается отношение напряжений в материале пластинки у кромки круглых включений к внешнему растягивающему усилию о/ p . Линии с маркерами в виде точек характеризуют величину о/ p для достаточно большого момента времени t = 10 9 с, а без маркеров - для нулевого t = 0 с момента времени. Эпюры построены в полярной системе координат.

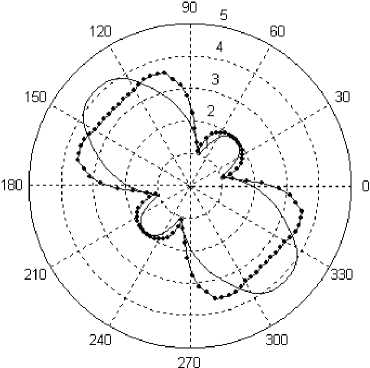
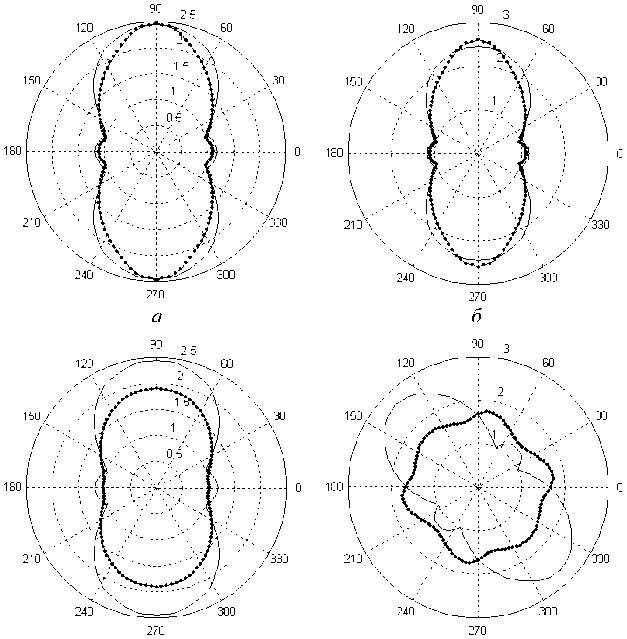
На рис. 2 приведены эпюры отношений окружных напряжений к внешнему усилию о ₀/ p , полученных при растяжении пластинки с круглым отверстием под углом 0° к одному из направлений упругости материала пластинки. Представлены результаты решения задачи при использовании всех независимых операторов (см. рис. 2, а ), при использовании только одного оператора сдвига (см. рис. 2, б ) и при аппроксимации всех операторов на основе одной функции (см. рис. 2, в ). Рис. 2, г . содержит эпюры отношений о ₀/ p , полученных при растяжении пластинки с круглым отверстием под углом 45° к одному из направлений упругости материала пластинки. Для получения окружных напряжений для отношений о ₀/ p , изображенных на этом рисунке, решалась исходная многооператорная задача (5) в общем виде. Из рис. 2, г хорошо видно, что напряжения в материале с течением времени претерпевают не только значительные количественные, но и качественные изменения.

Для количественной оценки эволюции напряжений у кромки отверстия построим график изменения параметра о0/p во времени (рис. 3). Линии 1, 2, 3 на рис. 3 соответствуют изменениям параметров о0/p, эпюры которых изображены на рис. 2, а, б, в, при угле, равном 90° (угол, при котором наблюдаются наибольшие напряжения). Таким образом, линия 1 соответствует решению задачи с использованием всех независимых операторов, линия 2 - решению задачи с учетом только сдвигового оператора и линия 3 - решению задачи при аппроксимации всех ядер операторов одной функцией. Значение с6/p = 2,8 соответствует упругому решению. Видно (см. рис. 3), что использование различных гипотез приводит к существенным количественным изменениям в результатах решений. Кроме того, можно говорить о большом росте напряжений во времени относительно упругого решения (до 40 %) (см. рис.3).

а

б

в

Рис. 2. Эпюры относительного напряжения П б/ p для задачи с отверстием

г

^ е/ Р

4.2

4.04

3.4

3.28

И 2.811-

7      8      9      10

Время t , с х 10^s

Рис. 3. Изменение относительного напряжения о_е/ p с течением времени для задачи с отверстием

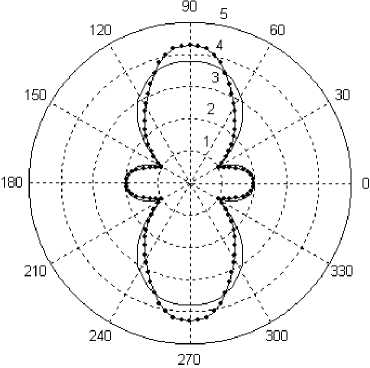
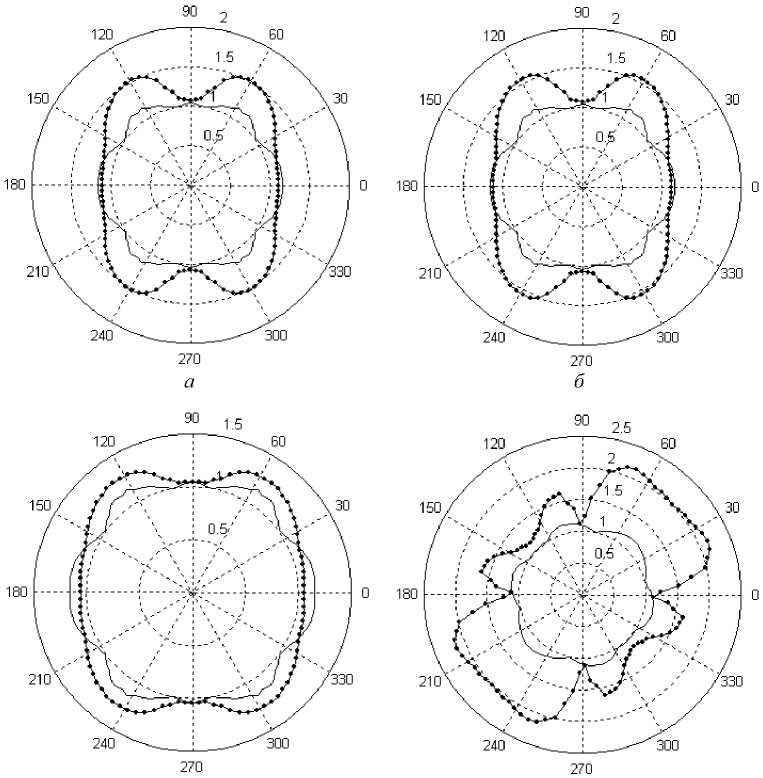
Приведем результаты решения поставленной задачи по растяжению пластинки с абсолютно жёстким включением. Аналогично рис. 2, на рис. 4, а , б и в изображены эпюры изменения параметра о_е/ p по углу при растяжении пластинки под углом 0° к одному из направлений ортотропии свойств материала пластинки. Эпюры получены при решении задачи с использованием всех независимых операторов, с использованием только одного оператора сдвига и с аппроксимацией всех операторов на основе одной функции соответственно. На рис. 4, г представлена эпюра с_е/ p для задачи о растяжении под углом 45° при учете всех независимых операторов.

На основании полученных картин (см. рис. 4) изменения отношения а_е/ p можно судить о наличии значительной эволюции напряжений в материале пластинки возле кромки жёсткого включения. Кроме количественных изменений напряжения претерпевают и значительные качественные изменения. В ходе работы выявлено, что окружные напряжения не только возрастают со временем, а еще и изменяют знак. Как и для задачи с круглым отверстием, различные гипотезы в постановке задачи приводят к расхождению в результатах решения.

Линии 1 , 2 и 3 на рис. 5 соответствуют изменениям напряжений а ₀/ p во времени, эпюры которых изображены на рис. 4, а , б , в , при угле, составляющем примерно 61 ° (угол, при котором наблюдаются наибольшие напряжения). Линия 4 рис. 5 указывает на значение о ₀/ Р ⁼ 0,116, соответствующее упругому решению задачи. Наличие точек графиков напряжений а ₀/ p (см. рис. 5), лежащих ниже линии 4 , указывает на то, что напряжения с течением времени меняют свой знак. Рост напряжений относительно упругого значения для данной задачи составляет около 450 % (см. рис. 5).

в

г

Рис. 4. Эпюры относительного напряжения o0jp для задачи с жёстким включением

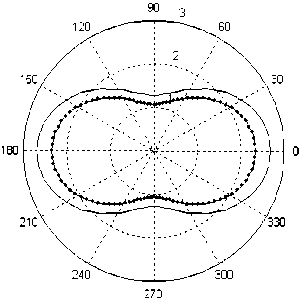
В отличие от задачи с отверстием, где на контуре отсутствует эффект перераспределения напряжений ( о r и т r ₀ равны нулю), для задачи с жёстким включением этот эффект имеет место. На рис. 6 приведены эпюры изменения по углу отношения радиальных напряжений о J p для задач на растяжение пластинки под углом 0° (см. рис. 6, а ) и 45° (см. рис. 6, б ). Из рис. 6 видно, что при увеличении окружных напряжений (см. рис. 4, а , г ) радиальные напряжения уменьшаются. Таким образом, в материале пластинки происходит перераспределение напряжений.

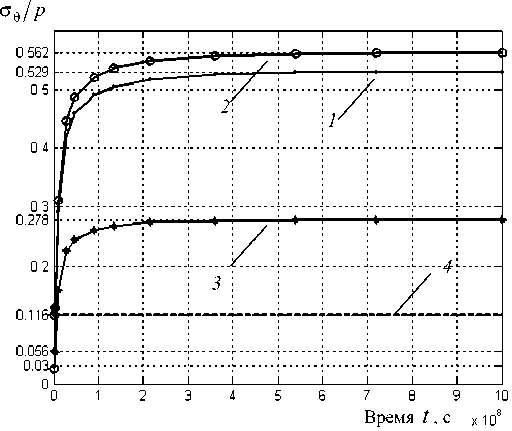
Рис. 5. Изменение относительного напряжения о₀/ p с течением времени

а

Рис. 6. Эпюры относительного напряжения о Jp

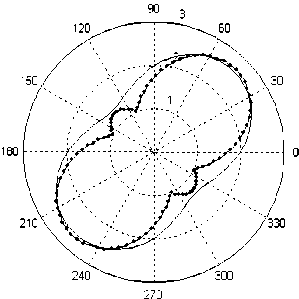
б для задачи с жёстким включением

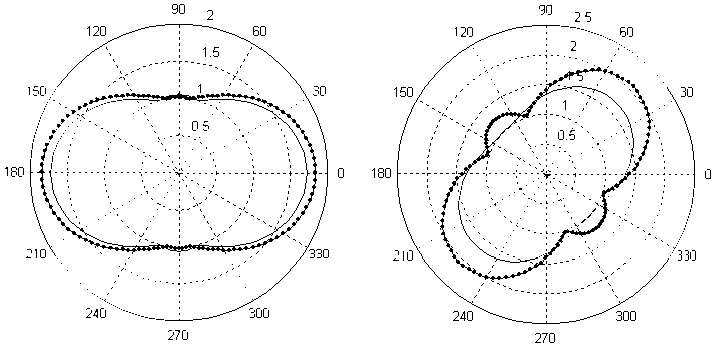
Приведем результаты решения задачи о растяжении пластинки с упругим включением, физические соотношения для которого приведены в (4). На рис. 7 приведены эпюры для отношения о₆/ p аналогично рис. 2 и 4. Видно, что перераспределение окружных напряжений у кромки включения невелико. Однако из рис. 7, в , видно, что при решении задачи с упругим включением использование описания всех операторов на основе одной функции приводит к значительному уменьшению окружных напряжений. С другой стороны, подобное уменьшение не наблюдается при решении задачи с использованием всех операторов. Следовательно, для данной задачи попытка аппроксимировать все операторы на основе одного не даёт качественно верного решения. Рис. 7, г показывает наличие заметного качественного и количественного изменения окружных напряжений возле кромки включения при растяжении пластинки под углом 45°.

в

г

Рис. 7. Эпюры относительного напряжения о₆/ p для задачи с упругим включением

Аналогично рис. 6 на рис. 8 изображены эпюры изменения по углу радиальных напряжений a _r/p возле кромки упругого включения для задач на растяжение пластинки под углом 0° (см. рис. 8, а ) и 45° (см. рис. 8, б ). Рис. 8. показывает, что при уменьшении окружных напряжений (см. рис. 7 а , г ) радиальные напряжения растут.

б

а

Рис. 8. Эпюры относительного напряжения a J p для задачи с упругим включением

Таким образом, в рамках данной работы поставлена и решена задача линейной вязкоупругости для ортотропной пластинки с включением при различных гипотезах учета вязкоупругих свойств материала пластинки. Установлен эффект значительного перераспределения напряжений в материале пластинки возле кромки включений даже при постоянной внешней нагрузке. Попытка применения различных упрощающих гипотез при описании вязкоупругих свойств материала приводит к существенным отличиям от решений в общей постановке и даже к качественно неверным результатам.