О периодических решениях одного класса линейных неоднородных систем обыкновенных дифференциальных уравнений с малым параметром в резонансном случае

В работах [1–3] рассмотрена задача о ветвлении периодических решений линейных дифференциальных уравнений в банаховом пространстве с вырожденным или тождественным оператором при производной и возмущением в виде малого линейного слагаемого. В работе [4] приведен пример одной линейной неоднородной системы обыкновенных дифференциальных уравнений с малым линейным возмущением, для которой справедливы результаты работы [3]. Расширим класс линейных неоднородных систем обыкновенных дифференциальных уравнений, для которых справедливы результаты работы [3].

Для этого рассмотрим класс возмущенных линейных неоднородных систем обыкновенных дифференциальных уравнений вида:

(*1\  / 0  а\ /хп _ /2  0 \ /хп _(“ Sin^t )

)■

\х2)   -—а  0^\х2)    ^0  -2)\х2) \ь Cos(t)t)

где Х[ Е R, е - малый вещественный параметр, а, Ь,а, ы Е R - фиксированные параметры, для которого параметры а и ы связаны соотношениями а = к ы,к = 2,3,.....

В обозначениях работы [3] найдем

» • = (-“   а ) , А= ( а 1 ) ,   » . = ( 2 —°₂ ) .   ^- (^)        (2)

и, следовательно, f(t) - периодическая вектор-функция с периодом Т = 2у .

Найдем собственные значения матрицы Ва:

L_a ( Л ) = В_а - ЛА = ( ^-Л  J^),     detL_a ( A~ ) = Л² + а² = 0, Л₁₂ = +1а.

Следовательно, имеется только одна пара чисто мнимых собственных значений матрицы Ва и ей соответствует пара периодических решений с периодом Та =~^ линейной однородной системы обыкновенных дифференциальных уравнений dy dt=B^

где у Е R².

Так как собственные значения Л12 матрицы Ва и период Т функции f(t) связаны соотношениями

,        2пк

Л1,2 = ±1—, то для линейной неоднородной системы обыкновенных дифференциальных уравнений dz          „ fa = BaZ- f(t),                                       (4)

где z Е R², согласно [5], имеет место резонансный случай.

Ставится задача [3; 6]: при достаточно малых вещественных е найти все Т- периодические решения x(t,E) уравнения (1), удовлетворяющих условию x(t, 0) = z(t), где z(t) - Т-периодические решения уравнения (4).

Для решения поставленной задачи применим методы теории ветвления, основанные на построении обобщенных жордановых наборов и исследовании разрешающих систем Ляпунова-Шмидта в корневом подпространстве [1-3; 6].

Найдем элементы В₁-жордановой цепочки оператора Ва

Vari = ^a,Va = [ ^Ba^-4] = [ ⁽°a )Hl 1 ) dt ] '                 ⁽⁵⁾

Будем искать ^ ^{( 1 )} в виде ф = ( а ^ ) е^{1 а,:}. Подставляя в уравнение (5) получим

Ф ^ ¹ = а₁ (^) е^1М, где а₁ Е С.                                 (6)

Найдем р ( ^{2 )} как решение уравнения

Sg^i = Bip1\ где B1 и В0 определяются по формуле (2) и (5) соответственно.

Имеем

(^ = ^a1 (ia + i ) ^eiMt’^{а2 Е С}'

Так как уравнение Вор^3) = B1pl2) не имеет решений, то длина Bi-жордановой цепочки оператора Bg равна рг = 2.

Аналогично, найдем B 1 - жорданову цепочку оператора

В В - ^ dt=^

0   а

—а 0

W¹ °1- )   ( о 1 ) dt

! ^{( 1 )} = c1 (1) e^iat,

^⁽²⁾ = C 1 (.    ² 2 ] e^iat,     C1,C2£C.

V ^iC2 ^— aJ

Найдем элементы z® £ Е_2п и у® £ Е_1п согласно работы [1]

z 11) = ^B 1 P ⁽ ₁ ^{2 )} = ^2а 1 ⁽ . ² 2 )

\—‘а2—а

Y¹^ B-^ = 2C1( ,^Ci 2 )

К ^—iC2^—a _

e^iat,  z® = B₁p l ^{1 )} = 2a1

e^iat,  у ( ^{2 )} = B^¹ = 2c 1

(- i ) ( —i )

eiat

eiat

Коэффициенты a^Ct (i = 1,г) подбираем из условий биортогональности [3].

Вычислим

«р_: - .у_: - » ⁴;y

« p l ^{1 )} ,y l ^{2 )} »= 0;

«р^г^4^^

—-1; а J

«zM1^4^;

«z <¹⁾,^⁾ »=⁴^ [ a₂₊C₂

« z j ² ) .!^ ! ¹ ) »= 0;

—

где

«р^.у^ »=

4a1C1i -------------------;

а

« z ( ^{2 )} ,^ ( ^{2 )} »=

4a₁C₁i а '

«f-9

1 Г

»=^J < f,g> dt

Получим систему уравнений

4a1C1i а

4a 1 C 1 i ₌ а

2i az + C2 -- а

= 0.

Представим вектор функции f(t) в экспоненциальной форме f«>-1(-“(T)'-- О)

и вычислим

«j7-1

2п

Mfu

»=^~l dt =

2л Jо         ¹

с^а + ^Ъ) , 12_П(_к-1) _ а 4л(к - 1) ^(е           1)

_

^_^((>-12^+1) _П-0

4л(к + 1) ^(е           1)

Аналогично вычислим

2п

«f.-a»=£(“ >dt =

2л Jo

^сС^Сгкш^            -   с(Ск^^-Ь)_:+^      -

4тгкм(к — 1)                  '      4пкы(к + 1)

= 0.

Учитывая (12) и (13), найдем

-11-^^+^)

1 — £²                  1г

{11 =^— « f,hn »= — ^2 [« f,-^ » +£ « f,—2 »] = 0, и, следовательно, {и = 0.

Тогда согласно работы [3] система (1) имеет аналитическое по £ единственное Т- периодическое решение

x(t, £) = yz7 [{ц^к1) + SiiVk1] + 772 [{ц^к2) + {и<Рк22] + у№ = y(t), где

y(t) = [I — £roBi]-1rof(t).(15)

Здесь Г—¹ = Bo, Bo = B o +«^,y 1 ¹⁾ » z^+ «•.у^ » z^.

Преобразовывая уравнение (15), получим

ВоУ = £Byy + f(t).

Решение уравнения (16) ищем в виде

^y ( ^t ) = e '“‘ (d 1 ) ₊ e^- '“' (d 2 ⁾ .

где d_iE C, i = 1,2.

Подставив y(t) в уравнение (16), получим

[(Л ;^{) —i} “ ^—£ ( 0 -2)]$У‘⁺«^е‘^ш^^^               ⁽¹⁷⁾

+<< е“ (‘d),f^1) » zf + [(

—а

а) , ■

0) + i"

-

г(0

g —itot I

Приравнивая коэффициенты при eiWt и е iWt в левой и правой частях уравнения (17), получим следующую систему уравнений:

[(0 a) + iw —г(2 °)] ^MO

Lx —а  0/         x0  —2/J yd₂/    2 \ Ь J

Выделяя вещественную

и мнимую часть dj = d⁽¹⁾ + id⁽², получим

следующую

систему уравнений:

(

—2г	а	ы	0
—а	2г	0	ы
—ы	0	—2г	а
0	—ы	—а	2г

)

d^ d2n

d?

² _{а —} —

.

Так как при г < ^-^(к²

-

W) \₀ ² )

1) , то определитель матрицы системы (19)

△ = 16г4 — 8Е2к2ш2 + 8г2ы2 — 2к2ы4 + к4ы8 ^ 0,

И, следовательно, система (19) имеет единственное решение. Решая ее при а = кы получим:

" 1 ы(а + кЬ)

d =

2 4г2	— ы2(к2 — гЬ	-1)
4г2	— ы2(к2 — га	1)
4г2 1	— ы2(к2 — ы(ка + Ь)	1)

L2 4г2

-

ы2(к2 - 1) J

■

Следовательно, Т-периодическое решение системы (1) имеет вид

-•'>=(»=(.

V

ы2(к2 — 1) —4E2Sin(wt)

ы2(к2

ы(а + кЬ)

___ы(ка + Ь)_____ ы2(к2 —1) —4г2 ( ) ы2(к2

— 1) — 4г2 га          ,

— 1) — 4г2 ‘

Cos(wt)

2Cos(wt)

)

Учитывая, что при г = 0 уравнения (1) и (4) совпадают, находим, что их однопараметрическое семейство вещественных Т-периодических решений представимы в виде [3]

x(t, 0) = z(t) = с[^(1) + «р^1)] + Го/,

где с Е R .

Найдем и = F0f(t) . Представим это уравнение в виде Вои = f(t), или

Вои+« и,у(1 » z(1)+ << и.у^ »

Представляя решение в виде

^ = f.

u=в,"t(d1)+e-'"t(d1)■

и подставляя в систему (21) получим

-^

d =

.

\

a

2ko '

2^Sin(mt)

— Cos(ot)

Sin()) — 2k)

Cos(ot')

)

.

Параметр a1 в формуле (6) подберем из условия, что ||<р(1)| = 1. Этому условию удовлетворяет a1 = 1=.

Следовательно,

^T^^’

Подставляя (23) в (22) получим, что однопараметрическое семейство вещественных Т -периодических решений системы (1) при £ = 0 имеет вид

z(t) = с^2 (

Cos(kot) Sin(kot)

Ъ

~2кш Sin()t) — Cos(ot) Sin(wt) — O^cc Cos(ot)

).

Построим графики компонент решений систем (1) и (4).

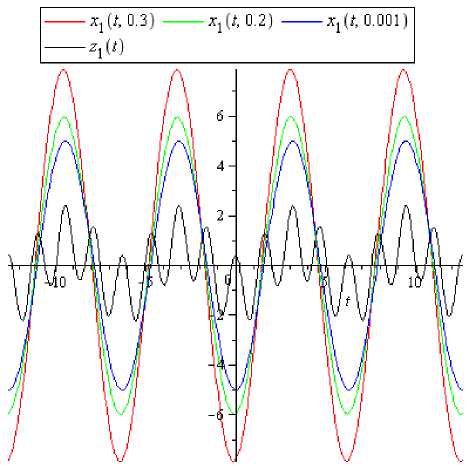
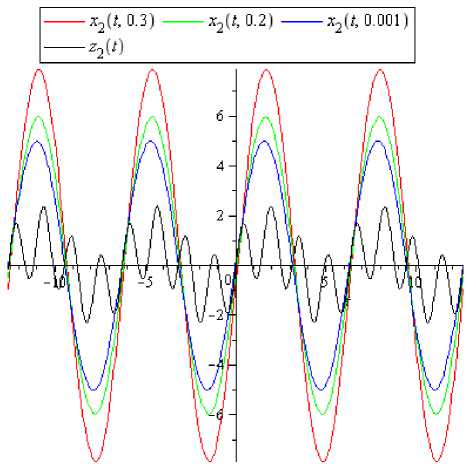
Рис. 1. Графики компонент X 1 (t, г) и X 2 (t, г) решения системы (1) при различных г и компонент z 1 (t) и z₂ (t) решения системы (4) при с = 4.

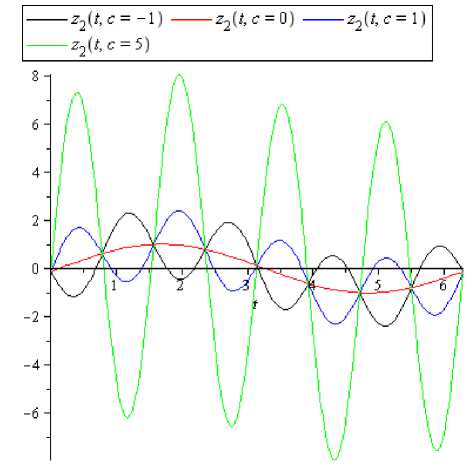
На рисунке 2 представлены графики z(t) при разных значениях с.

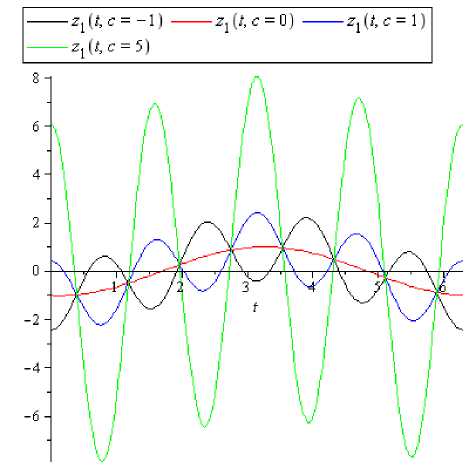
Рис. 2. Графики компонент z 1 (t) и z₂(t) решения системы (4) при различных с.

--- [^(^=^(0^ = 2] --- [хД^еХ^^гХе^Д]

----[Md,^), c=0.1]----[z.(r),z,(f), c=Q.?]

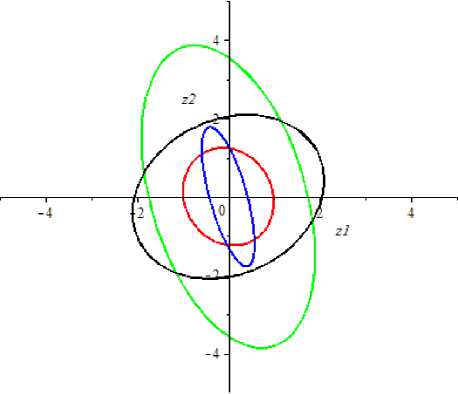
Рис. 3. к = 1: графики периодических траекторий системы (1) при г = 0,1 и системы (4)

при различных с.

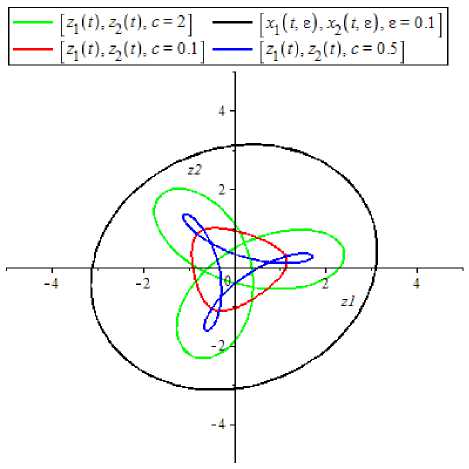
Рис. 4. к = 2: графики периодических траекторий системы (1) при г = 0,1 и системы (4) при различных с.

Таким образом, для класса линейных неоднородных систем обыкновенных дифференциальных уравнений вида (1) с малым линейным возмущением построены периодические решения в резонансном случае. Показано, что в случае, когда малый параметр равен нулю, появляется однопараметрическое семейство периодических решений.