О первых интегралах гамильтонных систем в симплектической геометрии

Пусть дано гладкое многообразие M . Скобка Пуассона на M сопоставляет каждой паре гладких вещественнозначных функций новую гладкую вещественнозначную функцию, которую мы будем обозначать через {F, Н} Чтобы называться скобкой Пуассона, такая скобочная операция должна обладать определенными свойствами. Мы сформулируем эти свойства сначала в простом бескоординатном виде. Впоследствии мы перепишем их в локальных координатах, и в таком виде их также можно взять в качестве определяющих свойств скобки Пуассона, особенно если M - открытое подмножество некоторого евклидова пространства.

Определение. Скобка Пуассона на гладком многообразии M — это операция, сопоставляющая каждой паре F, Н гладких вещественнозначных функций гладкую вещественнозначную функцию ^{ F ^, Н ^} на M и обладающая следующими свойствами:

• (а)    билинейность:

{cF + с'Р, Н} = с {F, Н) + с'{Р, Н},

{F, сН + с ’ Р} = с{ F, Н} + с' {F, Р} для любых с, c ^  ;

• (b)    кососимметричность:

{F, Н} = -{ H, F};

• (c)    тождество Якоби:

{{F, Н}, P} + {{ P, F}, H} + {{H, P}, F } = 0;

• (d)    правило Лейбница:

{ F , H • P } = { F , H } • P + H • { F , Р}.

(Здесь • обозначает обычное умножение функций.) Во всех этих равенствах

• F, Н и Р — произвольные гладкие вещественнозначные функции на M .

Многообразие M со скобкой Пуассона называется пуассоновым многообразием, а скобка определяет пуассонову структуру на M . Понятие пуассонова многообразия является несколько более общим, чем понятие симплектического многообразия или многообразия с гамильтоновой структурой; в частности, многообразие не обязано быть четномерным.

Пусть M - четномерное евклидово пространство R² n координами

⁽ p , q ) = ⁽ Pi ,..., p _n , q i ,-, q _n )

Мы определяем Скобку Пуассона двух гладких функций

F (p, q), H(p, q)

формулой (канонической скобкой

пуассона)

n

{F, Н} = X< i=1

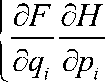
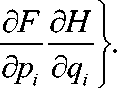
Гамильтоново векторное поле:

Определение. Пусть M — пуассоново многообразие и H: M ^ R — гладкая функция. Гамильтоновым векторным полем, соответствующим функции H, называется единственное гладкое векторное поле vH на M, удовлетворяющее условию vH (F) = {F, H} = -{ H, F } для каждой гладкой функции F: M ^ R. Уравнения потока векторного поля vH называются уравнениями Гамильтона для «гамильтониана» H.

Пример:

В случае канонической скобки Пуассона (1) на Rm, m = 2n +1 гамильтоново векторное поле, соответствующее функции  H (p, q, z), очевидно, имеет вид n ( дH d  дH t! ^ф7  -W dps,

Рассмотрим систему гамильтоновой форме

обыкновенных дифференциальных уравнений в

— = J (x )V H (x, t)

где H ( x , t ) — гамильтониан, a J ( x ) — структурная матрица, задающая скобку Пуассона.

Пример. На плоскости гамильтоновым векторным полем, соответст-

1/2,  2А      _                    дд вующим функции   H (x, у) = — (x + у ) имеет вид  vH =-у+

2                               д x    д у

Соответствующая гамильтонова система дифференциальных уравнений

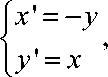
Определение. Функция P (x, t) называется первым интегралом системы (2), если для решения x (t) имеет место P(x(t), t) = const для всех t

Для системы (3) функция   H(x,y) = ^(x2 + у2) является первым интегралом. Первые интегралы легко описываются с помощью скобки Пуассона. Известна следующая теорема о первых интегралах системы (2).

Теорема-1. Функция P(x, t) является первым интегралом гамиль- тоновой системы (2), если и только если дР

— + { P , H } = 0    (4)

dt для всех x, t. В частности, не зависящая от времени функция P(x) является первым интегралом в том и только в том случае, если {P, H} = 0 всюду.

Из этой теоремы вытекает следующее следствие.

Следствие-1. Если гамильтониан H(x) гамильтоновой системы (1) не зависит от времени, то он сам автоматически является первым интегралом.

В самом деле функция  H(x,y) = !(x^ + yД также является первым интегралом системы (3).

Следствие-2. Любая отмеченная относительно скобки Пуассона, заданной матрицей J , функция C ( x ) является первым интегралом гамильтоновой системы (1).

Мы доказываем следующую теорему.

Теорема-2. Предположим, что функция P(x, t) является первым интегралом не зависящей от времени гамильтоновой системы. Докажите что дР д2 Р ее производные —, —— и т.д. также является первыми интегралами.

д t   д t2