О подборе параметров многослойной резонансной ультразвуковой камеры

В работе [1] рассматривалось поле звука конечной амплитуды в многослойной ультразвуковой камере, для которой справедливо предположение о плоском движении. При этом было принято предположение об идеальности границ (абсолютно жесткая при a = 0 и абсолютно мягкая при a = L , где L — размер камеры). При таком предположении на собственных частотах камеры возникает резонанс, и амплитуда вынужденных колебаний стремится к бесконечности. Тем не менее, такая постановка задачи была оправдана для максимально возможного упрощения задачи при анализе происходящих в ней физических процессов. В ряде работ [2-5 и др.] краевое условие на границе жидкости с воздухом принималось не идеальным (абсолютно мягким), а импедансным, что приводит к резонансам с конечной амплитудой и тем самым к возможности резонансного озвучивания камеры. Это, в свою очередь, позволяет получать максимально возможные значения радиационного давления в камере. В настоящей работе рассматривается возможность сопряжения на открытом конце камеры с произвольным жидким полупространством. Изучаются возникающие при этом возмущения поля стоячей волны, а также даются рекомендации по подбору параметров слоев камеры для локализации микрочастиц в поле радиационного давления звука, вызываемого как стоячей, так и возникающей в камере с потерями бегущей волнами.

ПОСТАНОВКА ЗАДАЧИ

Пусть, как и в [1], задана труба конечной длины L , заполненная жидкостью с переменными плотностью р0(a) и скоростью звука c0(a), относящимися к равновесному состоянию среды. При a = 0 установлен поршень, осуществляющий вы нужденные гармонические колебания частотой to , а со второй стороны при a = L жидкость граничит либо с воздухом, либо с другим жидким полупространством, и в отличие от [1] задано не идеальное, а импедансное краевое условие. Для акустических колебаний по-прежнему справедливо допущение о плоском движении, т. е. зависимость от одной переменной. Независимая переменная a рассматривается в лагранжевых координатах и привязана к конкретным частицам среды, находящимся в равновесном положении в точках a е [0, L ].

Функции р ₀( a ) и c ₀( a ) могут либо быть, по крайней мере, однажды дифференцируемыми, либо иметь разрывы первого рода, в частности быть кусочно-постоянными.

Необходимо выявить степень различия решения поставленной в настоящей работе задачи от решения задачи с идеальными краевыми условиями, полученными в [1].

РЕШЕНИЕ ЗАДАЧИ

Будем рассматривать установившиеся колебания для амплитуды акустического давления и колебательной скорости только для первой гармоники. Значения соответствующих величин для второй гармоники легко вычисляются после вычисления амплитуд первой гармоники. Здесь и далее для удобства будем учитывать временной фактор в виде e - ^{i to t} :

p ( a , t ) = P ( a ) e - ^{i to t} , v ( a , t ) = V ( a ) e - ^{i to t} , (1)

где P(a) и V(a) — амплитуды акустического давления и колебательной скорости. Отметим, что в физическом результате следует принимать p (a, t) = Re( P (a) e -itot), v (a, t) = Re(V (a) e -itot).

Уравнение для первой гармоники акустического давления имеет вид (см. (23) в [1])

D ( P 1 ) = d P ^{1   d p o} dP + k ² ( a ) p 1 = o.    (2)

d a ² p ₀(a ) d a d a

вид

^P 1 ⁽ a ) = ^mP o ^{(o) v} o G ⁽ a , ° ^m ) = ^{i m}P o ^{(o) v} o ^-^^a ;

w ^{( m ,o)}   (₆)

a е [o, L ],

Для краевого условия при a = 0 с учетом (1) имеем (см. (24) в [1])

где

d P ( a ) d a

= i top o (0) v o , a = 0

1 У 1 ⁽ a ) У d ⁵ )-   ^a ^ ⁵

^{w (} m 5 ) у Д ⁵ ) У 2 ⁽ a ),   a ^ ⁵

где v ₀ — амплитуда колебательной скорости поверхности поршня. Как показано в [1], уравнения (2), (3) сводятся к следующему виду:

—--^dR dP + k 2( a) P1 = da    p 0( a) d a d a

= i mp o (O) v o 5 ( a );                              ^(2а)

d p d a

= o.

a = o

(3а)

Поставим краевое условие на границе a = L . Пусть акустический импеданс Z * полупространства a е [ L , ” ) равен Z ' = p ' c ' . Тогда на границе a = L должно выполняться условие непрерывности импеданса

y 1 ( a ), у ₂( a ) — решения уравнения (2), удовлетворяющие соответственно краевым условиям (3) и (3а); w ( m , 5 ) — вронскиан этих решений.

Таким образом, возмущение краевого условия (3а) приводит только к возмущению решения у ₂( a ), а следовательно, и вронскиана.

Вначале рассмотрим случай контакта жидкости с воздухом. Учитывая малость параметра £ , можно искать решение у ₂( a ) методом возмущений:

у ₂( a ) = у ^(o) ₂( a ) + £ у ⁽¹⁾ ₂( a ) + £ ² у ⁽²⁾ ₂( a ) + ... (8)

Подставляя (8) в (2), (3 а), получаем систему рекуррентных краевых задач:

P ( L )/ V ( L ) = Z * ,                  (4)

где P ( L ) и V ( L ) — значение амплитуд давления и колебательной скорости жидкости на границе с полупространством. Исходя из известного соотношения [6]

D ( у ^(o) ₂( a )) = o,

D ( у ^{( 1} )2 ( a )) = o, 1 = 1,2,...

у (0)2( a )|    = o;(9а)

a=L f у-( a) + A = o, da ,. .

V                        J a=L(9б)

V ( a ) =

d P /d a i mp (a ) ’

приходим в (4) к краевому условию третьего рода

f_D/ .    d P ( a )A

I P ( a ) + £ —— I d a

\                    / a = L

= o,

где

£ = i

Z mp( L)

(4а)

Здесь D (^) — дифференциальный оператор из (2).

В случае кусочно-постоянных скорости звука и плотности возмущенное решение у ₂( a ) может быть найдено проще. Пусть камера состоит из n слоев жидкости с кусочно-постоянными акустическими характеристиками. Рассмотрим n -й слой жидкости, граничащий с воздухом. Решение у ₂( a ) в этом слое с точностью до постоянного множителя равно (из двух возможных представлений [7, с. 146] выбираем именно такое из физических соображений)

При £ = o краевое условие (5) соответствует идеальной абсолютно отражающей границе жид-кость—вакуум. Отметим, что, как видно из (4а), реально возмущение краевого условия зависит от

Z *

соотношения а = z ( l ) , где Z ( L ) — акустический импеданс жидкости в камере на границе L .

Согласно [1], решение задачи (2), (3), (3а) имеет

e lk» ⁽ a - L ) + v _e - ik n ⁽ a - L )

у 2 (a ) =--------- =

2 i

-Veikn(a- L) + Ve-ikn(a- L)

=__I__ e ik n ⁽ a ^L ) =

2 i2

= -V sin k„ (a - L) + 1+V eikn(a-L).

2 i

Известно, что коэффициент отражения равен [6]

z -z

V = ^{в n}

где Zn= ρncn — импеданс n-го слоя жидкости. Подставляя (11) в (10), получаем y2(a) = -Vsinkn(a - L) +1eikn(a-L)( Zв )= iZn + Zв

=-Vsinkn(a-L)+1eikn(a-L)∑∞ αl = n                 i

=-Vsinkn(a-L)+1eikn(a-L) α = n         i1

=-Vsink(a-L)+α1eikn(a-L)+O(α2), ni где

α=Zв /Zn(13)

отношение импеданса воздуха к импедансу смежного с ним слоя жидкости. Например, для воды α = O (10 ^{- 4} ) , а V = - 0.999428 . В случае контакта с воздухом жидкости с большими значениями плотности и скорости звука возмущение решения еще меньше. Решение y ₂ ( a ) в остальных слоях находится по методике, изложенной в [1]. Очевидно, что в остальных слоях возмущение решения также имеет порядок O ( α ), о чем свидетельствует и характер рекуррентных соотношений в краевых условиях (9б). Таким образом, возмущение решения имеет порядок O ( α ) и практически может не учитываться ввиду малости α .

Иначе обстоит дело с вронскианом. Здесь ситуация вследствие возмущения краевого условия (3а) меняется качественно. В отсутствие возмущения краевого условия при a = L камера представляет собой ограниченный резонатор с идеально отражающими границами, и на частотах его собственных колебаний возникают резонансные колебания бесконечной амплитуды, что, как видно из (7), соответствует нулям вронскиана. При наличии возмущения краевого условия камера фактически становится полубесконечной, на границе с воздухом происходит просачивание энергии и резонансов с бесконечными амплитудами не возникает. Однако возникают конечные резонансы, которые связаны с минимумами модуля вронскиана в (6). Ниже рассмотрим методы нахождения резонансных частот, здесь же сделаем замечание относительно степени возмущения значения вронскиана.

Во-первых, вследствие того, что функция y1 (a) является действительной, вронскиан возмущенной задачи, как видно из (12), становится комплексно- значной функцией. Во-вторых, у вронскиана возмущенной задачи отсутствуют нули, т. к. в противном случае это означало бы бесконечность энергии в системе с потерями (впрочем, это можно объяснить и из математических соображений: функции, описывающие стоячие и бегущие волны, не могут быть линейно зависимы). Нули вронскиана невозмущенной краевой задачи возникали при условии, когда решение y1 (a) в n-слое равно y1(a) =γy2(0)(a) =γsinkn(a - L).        (14)

Подставляя y ₁( a ) из (14) с γ = 1 и y ₂ ( a ) из (12), получаем, например, в случае однослойной камеры возмущение вронскиана относительно нулевого значения:

w(ω,ξ) = dy (kξ)         dy (kξ)

= y ₁( k ξ ) ² - y ₂ ( k ξ ) ¹ = ik α .    (₁₅)

dξdξ

Таким образом, в этом случае вронскиан получает чисто мнимую добавку, пропорциональную частоте и параметру возмущения.

При не малых значениях α применять теорию возмущений неправомерно, поэтому резонансное решение будем находить иначе, о чем будет сказано ниже.

Поскольку при использовании камеры на резонансе важно уметь находить резонансные частоты, обратимся теперь к способам их отыскания. Рассматривать будем оба случая: как при наличии, так и в отсутствие потерь в ультразвуковой камере.

СПОСОБЫ ОТЫСКАНИЯ РЕЗОНАНСНЫХ ЧАСТОТ

Резонансные частоты как особые точки поведения вронскиана

В системе без потерь, как известно, резонансные частоты совпадают с нулями вронскиана, который является в этом случае действительнозначной функцией. В системе с потерями, как видно из (6) (или (12) в случае воздушного полупространства), модуль амплитуды стоячей волны в функции P ₁ ( a ) достигает максимума в точках локальных минимумов модуля вронскиана, который в рассматриваемом случае всегда больше нуля.

Нахождение резонансных частот с помощью дисперсионного соотношения

Подобный подход уже использовался в работе [1] при анализе распределения акустического поля в многослойной ультразвуковой камере и идеологически восходит к методу нахождения собственных значений в океанических волноводах методом решения дисперсионного уравнения [6, с. 221, 223]. Здесь обоснуем подход, использованный в [1]. В работе [6, с. 285] приведены соотношения, связывающие вронскиан с соответствующими коэффициентами отражения. В частности, можно записать

У 1 ⁽⁰⁾ У 2 ⁽ a ) = w ( to ,0)

=____________ (1 + V - (0)) У ₂( a ) ____________

(1 - V - (0) V + (0))( ik ( to , 0) y 2 (0) + y 2 (0)) ■

Здесь V (0) — коэффициент отражения плоской волны, падающей справа налево на поршень из однородного полупространства а е [0, ” ) с акустическими характеристиками примыкающего к поршню слоя; V + (0) — коэффициент отражения плоской волны, падающей слева направо из однородного полупространства а е ( -” , 0] с акустическими характеристиками примыкающего к поршню слоя на систему (слои—примыкающее к ним однородное полупространство с импедансом Z ' ). Как видно из (6) и (16), максимальной амплитуды поле в камере может достигать при условии

• 11 - V- (0)V+ (0)| = min,(17)

что равносильно условию arg(V-(0)V+ (0)) = 2mn, m = 0,1,2,...(18)

В системе без потерь (17) достигает нуля, в противном случае — всегда больше нуля. Отметим, что, по определению, V - (0) = 1. Тогда имеем:

arg(V+ (0)) = 2mn ,    m = 0,1,2,...,(18а)

что равносильно условию

• V+ (0) = V (0)|, Im(V+ (0)) = 0.(18б)

Соответственно минимальной амплитуды в камере поле достигнет при условии

• 11 - V. (0)V+ (0)| = max,(17а)

что выполняется, когда набег фазы кратен нечетному числу п :

arg(V+ (0)) = (2 m + 1)п, m = 0,1,2,...,(18в)

что равносильно условию

• V+ (0) = -V+ (0)|, Im(V+ (0)) = 0.(18г)

Рассмотрим исходное неоднородное полупространство а е [0, ”), а в нем один (любой) из n жидких слоев, например под номером I. Обозна чим через V- коэффициент отражения плоской волны, падающей на первые I -1 слоев справа налево из гипотетического жидкого полупространства с акустическими характеристиками I-го слоя. Через V1+ обозначим коэффициент отражения плоской волны, падающей на оставшиеся n -1 слоев и однородное полупространство с импедансом Z* слева направо из гипотетического жидкого полупространства, простирающегося до -”, также с акустическими характеристиками 1 -го слоя. Эти коэффициенты равны соответственно [5]

7 ^{(1 - )} — 7            7 ^{( 1 + )} — 7

V = Z BX Z 1 V = Z вх Z 1

^{1 -} Z вх^{(1 - )} + z ’     ^{1 +} Z_ra^{( 1 + )} + Z 1 ’

где Z₁ = p c — импеданс слоя 1 ; Z_x ^{( 1} ± ) — входной импеданс на границе l и l + 1 слоев при падении плоской волны слева направо (знак +) и на границе l - 1 и l слоев при падении плоской волны справа налево (знак - ) соответственно. Рассуждая аналогично тому, как в случае получения условия (17), получим необходимое условие для резонансных частот в таком виде:

^arg^{( V} 1 - ⁽ f ^)V + ⁽ f ) ^exP^{(2 ik} 1 ⁽ f ) d 1 )) = ^{2 m n} , m = 0,1,2,...,

т. е. таких частот, при которых происходит кратный 2 п набег фазы плоской волны, переотра-жающейся внутри рассматриваемой системы слоев. В этом случае происходит когерентное сложение волн. Здесь k , d — волновое число и толщина слоя соответственно; f — частота.

В системе без потерь резонансные частоты суть решения дисперсионного уравнения [6]:

• V - ( f )V + ( f )exp(2 ik, ( f ) d ) = 1.         (21)

Уравнение (20) для жидкого слоя, примыкающего к поршню, имеет вид arg(V+ (f) exp(2i^ (f) d 1)) = 2 mn, m = 0,1,2,...

Здесь учтено, что V - ( f ) = 1. Коэффициент отражения V ₊ ( f ) может быть найден из соотношения (19). Тогда имеем

(2 + )

ТЛ _ Z BX Z 1

¹⁺" Z J²⁺⁾ + Z ■ вх

Здесь Z_ex ^{(2 + )} — входной импеданс системы (жидкие слои—исходное полупространство) при а = d ; Z ₁ — импеданс примыкающего к поршню слоя.

Нахождение резонансных частот с помощью перерасчета входного импеданса

Z вх (2) = а ⁽²⁾ + ib ⁽²⁾,                     (27)

Пусть система из n слоев жидкости с постоянными акустическими характеристиками внутри каждого слоя и номерами l = 1, n граничит с двумя однородными полупространствами, которым припишем номера 0 (полупространство а е ( -” , 0]) и n + 1 (полупространство а е [ L , ” )). В работе [6, с. 21] приведена рекурсивная формула расчета входного импеданса системы таких слоев в случае падения исходной плоской волны из левого полупространства:

Z ( ₁ ) = Z x ^{( 1 + 1)} - iZ_t tg( kd ) Z ;

вх      Z, - iZ ex^{(1 + 1)} tg( kd ) ^{l ;}         (24)

Z x ^{( n + 1)} = Z n + 1 = Z * , l = i n .

Здесь d_l — толщина l -го слоя; Z_l = p c ; Z вх ⁽¹⁾ — входной импеданс системы, состоящей из n слоев и правого полупространства, рассчитанный на границе с левым полупространством.

Начнем со случая системы без потерь Z_{n + 1} = Z ' = 0. Как известно, в системе без потерь все входные импедансы, кроме ( n +1)-го, суть функции частоты с чисто мнимыми значениями. Обозначим Z_ex ⁽¹) = ib ⁽¹) , где b ⁽¹) — действительнозначные функции частоты. Воспользуемся соотношениями (22), (23). Тогда имеем

Z

^{2 k} 1 ⁽ f ) ^d 1 ^{+ 2arct}g⁽ b^) = ² m ⁿ .

Или окончательно

где a ⁽²⁾ — действительнозначная функция частоты. Подставляя (27) в (26) и далее в (18а), получим, согласно (18а), необходимое условие, которому должна удовлетворять мнимая составляющая коэффициента отражения:

Im( V + (0)) = у ( b ⁽²⁾ Z 1 tg ² ( k 1 d 1 ) - ( b ⁽²⁾ 2 -- Z 2 + a ⁽²⁾²)tg( k 1 d 1 ) - b ⁽²⁾ Z 1 ) = 0.

Здесь Y — действительный множитель. Как видно из (28), значение резонансной частоты вследствие появления отличной от нуля действительной составляющей импеданса в общем случае возмущается по сравнению с исходной системой без потерь. При а ⁽²⁾ = 0 решение (25) для невозмущенной системы будет удовлетворять (28).

Таким образом, резонанс возможен на такой частоте, когда выполняются условия (18а), (18б), т. е.

V + (0) = V .,

0 <  V , <  1.

tg( k 1 ( f ) d 1 ) + b   = 0.                 (25)

При V ₀ = 0 резонанса быть не может, т. к. вся энергия теряется, а при V 0 = 1 отсутствуют потери.

Обратимся теперь к поведению входного импеданса Z_ex ⁽¹⁾ , определяющего поведение V + (0). Согласно (26) и (29), мнимая составляющая импеданса Z_вх ⁽¹⁾ на резонансе должна быть равна нулю:

Im( Z x ^(V> ) = 0.                   (30)

Поведение действительной составляющей Z (1) вх найдем из условий (17) (при V- (0) = 1), и (26), и (30). Имеем на резонансе из (17)

Отметим, что при выполнении условия (25) становится равным нулю знаменатель в (24) при расчете (1) вх ^.

Получим аналогичные соотношения для системы с потерями. Для этого воспользуемся выражением (18а). Коэффициент отражения в начале координат V ₊ (0) при условии, что левее начала координат жидкое полупространство с характеристиками слоя, прилегающего к поршню, равен

V + (0) =

вх ^Z 1

Z ex ⁽¹⁾ + Z 1"

Известно, что в результате возникновения потерь входные импедансы (24) получают возмущение в виде отличной от нуля реальной составляющей. Пусть далее входной импеданс Z_вх ⁽²⁾ равен

-

Re( Z_в х ⁽¹⁾) - Z 1 _

Re( Z₆ x ⁽¹⁾) + Z 1

2 Z ₁

Re( Z x ⁽¹⁾) + Z 1

= min,

откуда, а также из (29) получаем условие, которому должно удовлетворять Re( Z_вх ⁽¹⁾ ) :

^{Re( Z} ex ^{(1) )} = max >  ^0.

Из тех же соображений, используя (17а), получаем, что при условии (18в) справедливо следующее равенство:

^{Re( Z} ex ^{(1) )} = min >  ⁰ .

(31а)

Таким образом, при набеге фазы в V + (0), кратном 2 п , для Z вх ⁽¹⁾ выполняются условия (30), (31),

а при набеге фазы, кратном нечетному числу п , для Z_вх ⁽¹⁾ выполняются условия (30), (31а).

Заметим, что для проводимости, являющейся обратной к импедансу величиной, ситуация меняется на противоположную: при набеге фазы, кратном 2 п (резонанс), действительная часть проводимости достигает минимума, а при набеге, кратном нечетному числу п (антирезонанс), действительная часть проводимости достигает максимума.

Отметим, что поскольку дисперсионное уравнение (21) является частным случаем (17), то для системы без потерь должны выполняться условия (30), (31). Условие (31) выполняется условно, т. к. в этом случае Re( Z_ex ⁽¹⁾ ) = 0. Согласно (25), входной импеданс Z_вх ⁽¹⁾ на резонансной частоте терпит разрыв второго рода. Слева и справа от точки резонанса Z_вх ⁽¹⁾ стремится к мнимым бесконечностям разного знака. Тогда саму точку разрыва можно условно трактовать как точку, для которой выполняется условие (30).

В работах [2, 3] приведена методика подбора параметров двухслойной камеры (толщины слоев и скорости звука в них), граничащей с воздухом, с использованием соотношения (25), пригодного для системы без потерь. Однако, как будет показано ниже, получающиеся при этом погрешности определения величины резонансных частот оказываются небольшими, ввиду малости возмущения. Впрочем, из текста работы [2] осталось непонятным, считает ли автор этой работы выражение (25) точным или все-таки приближенным для системы с потерями, каковой является рассматриваемая им модель.

ПОСТРОЕНИЕ ПОЛЯ СТОЯЧЕЙ ВОЛНЫ

Как отмечалось выше, при достаточно больших возмущениях граничного условия (3а) пользоваться представлением стоячей волны в слоях в виде (12) неправомерно, тем более что в этом случае не учитывается возмущение резонансной частоты. Для вычисления поля стоячей волны поступим следующим образом.

Пусть система исследуемых слоев граничит с однородным полупространством а е ( -” , 0] с характеристиками первого слоя. Пусть из этого полупространства на систему слоев падает слева направо плоская волна ₂ e ^{ik 1 ( f ) a} (далее аргумент f для краткости опускается). Тогда поле в полупространстве а е ( -” , 0] определяется выражением

У 1 ( а ) =

e 1 + V + (0) e - k ¹' ^-

.

Поскольку первый слой совпадает по свойствам с полупространством, то в первом слое поле также будет определяться выражением (32). Распишем (32) в следующем виде, также исходя из физических соображений (см. комментарий к (10)):

У 2 ( а ) = V (' e ₇"^+2 e*- (1 - V (0)) =

= V ₊ (0)cos( k 1 a ) + ⁽¹ - V ⁽⁰⁾⁾ e ^k'^- . (33)

Легко показать, что первое слагаемое справа в (33) с учетом временнóй зависимости в (1) и при условии Im( V (0)) = 0 в процессе сшивки решения от первого слоя к последующим будет продолжено решениями в виде сумм

• - l cos k— + b l sin k— , l = 2, n

с действительными коэффициентами a_l , b_l . На резонансе, согласно (18а), условие Im( V ₊ (0)) = 0 выполняется. Более того, как видно из (33), это слагаемое будет удовлетворять и левому граничному условию (3а). Таким образом, на резонансе первое слагаемое справа в (33), будучи продолженным в остальные слои, опишет стоячую волну. Второе слагаемое справа в (33), характеризующее бегущую волну, трансформируется в остальных слоях в бегущие в обоих направлениях волны. В полупространстве - е [ L , ” ) останется только бегущая вправо волна, образованная в смежном с этим полупространством n -м слое бегущими вправо волнами, включая и соответствующую составляющую стоячей волны.

Отметим, что стоячая волна формируется и при условии (18в), когда также выполняется равенство Im( V + (0)) = 0. Однако этот случай, согласно (16), (17а), соответствует минимальному значению амплитуды в камере (т. е. антирезонансу).

СОГЛАСОВАНИЕ ПРЕОБРАЗОВАТЕЛЯ С АКУСТИЧЕСКОЙ КАМЕРОЙ

Выше при определении резонансных частот было принято предположение о равенстве единице коэффициента отражения поршня (см. краевое условие (3а)). Однако на практике это условие может не выполняться. Реально источником высокочастотных колебаний применительно к рассматриваемой задаче может служить одна или несколько соединенных последовательно пьезоэлектрических пластин, подобранных таким образом, чтобы при подаче электрического поля в них возникали продольные упругие волны, параллельные электрическому полю и распространяющиеся вдоль толщины пластины. При больших волновых раз- мерах пластины считается, что в ней распространяется одномерная плоская продольная упругая волна [10, 11]. При расчете волнового поля в этом случае необходимо решать задачу об электромеханических колебаниях пластины, где помимо волнового уравнения с соответствующими механическими краевыми условиями необходимо учитывать пьезоэлектрические уравнения с соответствующими электрическими краевыми условиями [10]. Существует ряд подходов решения задачи расчета поля в системе пьезоэлектрик—резонатор. В частности, в работе [4] автор при решении подобной задачи для резонатора из трех слоев применяет метод передаточных матриц, развитый в работе [12]. О других подходах см. библиографию в [4].

В настоящей работе эта задача решаться не будет, однако покажем физику эффекта, описанного в [4], объясняющую причину того, что резонансная частота системы вибратор—многослойная камера лежит вне собственных частот вибратора. Для упрощения рассмотрим его в случае, когда пьезоэлектрическая пластинка заменена упругой однородной пластинкой с такими же механическими свойствами, как и в кристалле, и в которой присутствует только продольная волна. Пусть пластинка имеет толщину d , скорость продольных волн равна c_t и плотность р. Слева граница пластинки свободная (напряжение равно нулю). Справа пластинка нагружена на входной импеданс многослойной камеры, рассмотренной выше. Положим далее, что между правой границей пластинки и входным импедансом находится слой жидкости с импедансом Z 1 = р 1 с 1 (импеданс слоя жидкости, примыкающего к вибратору) исчезающей толщины. Резонансная частота в многослойной камере по-прежнему определяется выражением (17), где V (0) — коэффициент отражения плоской волны, падающей слева на пластинку. Найдем коэффициент отражения V (0):

пл

V (0) = -вх-----1,(34)

• - V / — пл + — рv 7

вх1

где Z_вх ^пл — входной импеданс пластины, который при условии левой свободной границы пластины равен, согласно (24),

• —_ю пл =- i—Jgkd , вх           пл

где — пл = pel; kl = to / cl. Как видно из (34), ImV- (0) = 0 только при условии tgkld = ±~, что п справедливо в случае kld = — + тп , или в терминах длин волн

• 2 т + 1

d = 4 X i , ⁽³⁵⁾ где X l — длина волны в пластинке. На частоте (35) V (0) = 1, и тем самым, согласно (17), наступает резонанс в многослойной камере. Отметим однако, что условие (35) соответствует собственным частотам пластины со свободной левой и защемленной правой границами [13]. Одновременно частота (35) является частотой антирезонанса пластины с обеими свободными границами. Это следует из выражения, аналогичного (20):

arg(VлеeVпрae exP(2М)) = (2m + 1)П, (36) т = 0,1,2,..., где Vле6 = Vnpa6 =-1 — коэффициенты отражения от левой и правой границ внутри пластины.

Поясним полученные результаты. Обычно резонансная частота вибратора измеряется либо на холостом ходу в воздухе (обе границы пластины не нагружены), либо одну или обе границы нагружают на волновое сопротивление воды в большой камере, где можно пренебречь отражениями. Волновое сопротивление воды на порядок меньше волнового сопротивления кварца [13, с. 205], и коэффициенты отражения на границе кварц—вода действительны и отрицательны. Поэтому резонансная частота однородной пластины, нагруженной на волновое сопротивление воды, совпадает с резонансной частотой ненагруженной пластины, что видно, например, из выражения (20) применительно к пластине.

Иное происходит, когда вибратор нагружен на резонансную нагрузку, каковой является многослойный резонатор. В этом случае на частотах, определяемых из условий (18а), (18б) (что равносильно частотам, на которых коэффициент отражения от системы слоев действителен и положителен), активный импеданс нагрузки на пластину может многократно превышать волновое сопротивление самой пластины. Поэтому коэффициент отражения на правой границе пластины действительный и положительный, что на антирезонанс-ной частоте ненагруженной пластины, согласно (36) (фаза экспоненты в (36) на антирезонансе не-нагруженной пластины кратна нечетному числу п ), будет соответствовать резонансу нагруженной пластины. Таким образом, на частоте, определяемой выражениями (18а), (18б), равной частоте антирезонанса ненагруженной пластины, возникает резонанс всей системы пластина—многослойная камера. Аналогично можно показать, что резонанс всей системы совпадает с резонансом ненагру-женной пластины, когда на этой частоте выполняется условие (18г), что соответствует отрицательному действительному коэффициенту отражения от системы слоев.

Табл. 1. Параметры многослойной камеры (в скобках представлены соответствующие величины для воздуха)

№ слоя	Скорость звука, м/с	Плотность, кг/м3	Толщина слоя, м
1	1500	1000	5∙10–3
2	5570	2600	1∙10–4
3	1500	1000	3∙10–4
4	5570	2600	1∙10–4
5	1500 (330)	1000 (1.3)	ГО

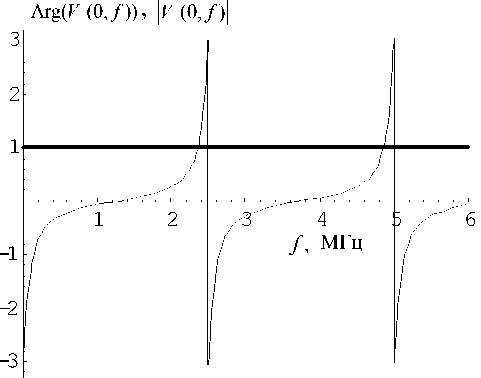
Рис. 1. Зависимость фазы и модуля коэффициента отражения пластины V - (0, f ) от частоты (34).

фаза,          модуль

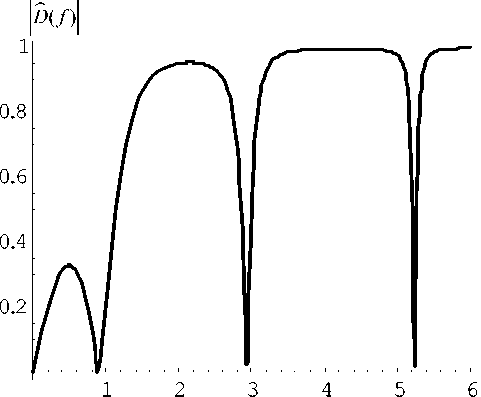
f , МГц

Рис. 2. Зависимость модуля функции D(f )

от частоты (38)

Однако резонанс всей системы вибратор—мно-гослойная камера происходит по частоте гораздо чаще, чем полупериод между резонансами вибратора. Согласно (17) и (20), резонансы возникнут на частотах arg(V- (0,fV (0,f)) = 2mn,      m = 0,1,2,... (37)

Здесь аргумент 0 в коэффициентах отражения означает, что они рассматриваются при a = 0 .

Ниже приведены зависимости аргумента и модуля функции, равной произведению коэффициентов отражения,

D ( f ) = V - (0, f )V (0, f ),            (38)

а также функции

D ( f ) = V (0, f ),              (38а)

удовлетворяющей условию (17) при V_ (0, f ) = 1. Многослойная камера имела параметры, приведенные в табл. 1, и граничила с водным полупространством. Пластина кварца имела следующие параметры: плотность 2650 кг/м³; продольная скорость звука 5710 м/с; толщина пластины 1.142∙10^–3 м, что соответствует основному собственному колебанию пластины на частоте 2.5 МГц.

На рис. 1 представлено изменение фазы коэффициента отражения (34) от пластины; там же приведен его модуль, тождественно равный единице. На рис. 2 представлена зависимость модуля функции D ( f ) (38), совпадающего с модулем функции D ( f ) (38а), от частоты. Видно, что модуль всей резонансной системы существенно зависит от частоты, а его поведение в данном случае зависит только от свойств многослойной жидкости.

I D ( f )|

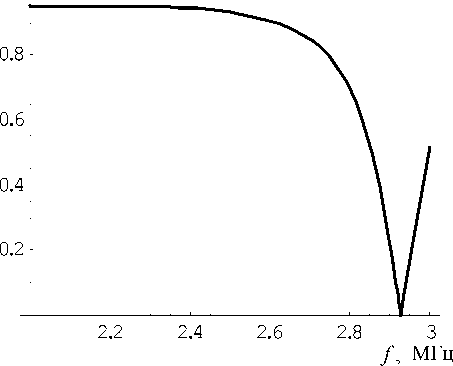
Рис. 3. Зависимость модуля функции D ( f ) от частоты (38)

I D ( f )|

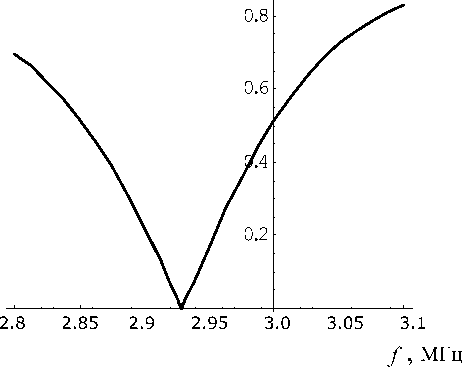
Рис. 4. Зависимость модуля функции D ( f ) от частоты (38)

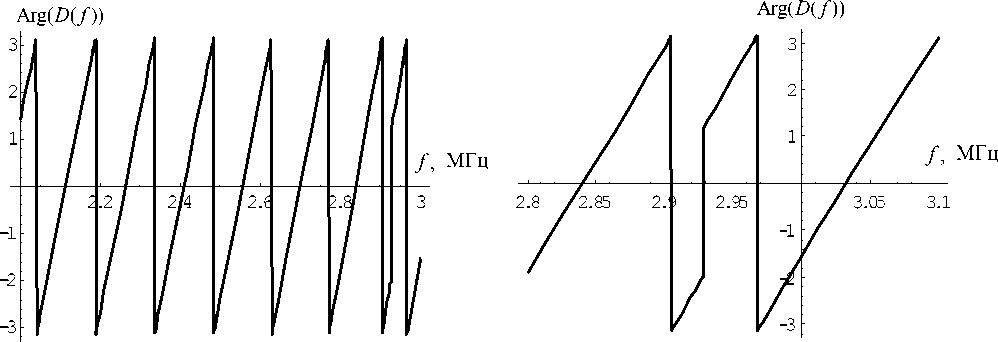
Рис. 6. Зависимость фазы функции D ( f ) от частоты (38а)

Рис. 5. Зависимость фазы функции D ( f ) от частоты (38а)

На рис. 3, 4 приведена та же зависимость, но в более узком частотном диапазоне. На рис. 5, 6 приведена зависимость фазы функции D ( f ) (38а) от частоты. Резонансные частоты соответствуют точкам с нулевой фазой. Из сравнения рис. 3, 5 и 4, 6 видно, что в точке, где модуль D ( f ) становится равным нулю, происходит скачок фазы этой функции на π . Это определяется свойствами многослойной жидкой камеры.

На рис. 7 показаны частотные зависимости фазы функций D(f) (38) и D(f) (38а). Видно, что учет резонансных свойств пластины возмущает значения резонансных частот всей резонансной камеры, однако на периодичность резонансных частот при этом влияния практически не оказывается. Видно также, что степень отличия значений резонансных частот меняется с частотой.

Приведенные рассуждения помогают понять физику явлений, происходящих в резонансной камере. Кроме того, построение модуля резонансной характеристики (38) позволяет выбирать резонансные частоты на участках, где этот модуль близок к максимальному.

Arg( D ( f )) , Arg( D ( f ))

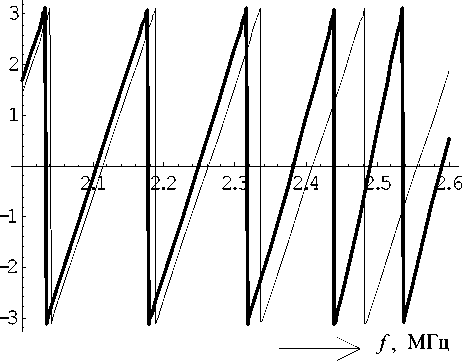
Рис. 7. Зависимость фазы функций D ( f ) (38)

и D ( f ) (38а)------от частоты

распределение амплитуды давления в слое имеет вид

P(а) = P0 cos(ka - ф), то тригонометрический множитель в (34) должен быть таким:

sln(2 kа - ф ).

Если известно пространственное смещение амплитуды давления

P(а) = P0 cos(к(а - а0)), то ф легко рассчитывается:

ф = ка ₀.

Когда бегущей волной пренебречь нельзя (коэффициент "бегучести" волны отличен от нуля), для определения радиационного давления можно воспользоваться формулой для произвольной волны ([8], см. также комментарии в [4]):

Для расчета реальной частотной характеристики резонатора, включающего конкретный вибратор, необходимо решать полную систему электромеханических уравнений [4, 10-12 и др.].

РАСЧЕТ РАДИАЦИОННОГО ДАВЛЕНИЯ

Сила радиационного давления, оказываемого полем стоячей волны на сферические частицы малого волнового размера, определяется следующим выражением [8]

F = 4 п К ² EkR sin 2 ka -

Pp + 2/3(Pp - P) 2 Pp + P

1 c ² P

³ c P ² P p

Здесь R — радиус сферы; E — средняя плотность звуковой энергии стоячей волны; к — волновое число в жидкости; c , P и c p , P p — скорость звука и плотность жидкости и частиц соответственно. Для средней плотности звуковой энергии в стоячей волне имеем [7, с. 114]

—    1 Р '

E =      ⁰

P c ² 4

Здесь P ₀ — амплитуда стоячей волны.

Выражение (34) справедливо в однородной среде. В рассматриваемом случае многослойной среды необходимо привязаться к узлам давления в рассматриваемом слое. Легко показать, что если

Ф ( а ) = - - nR

F = -^ф ( а ).

3( Х -1)- . . Г 1 У- .

--------E kin ( а ) - 1-- 7 E pot ( а )

2Х +1          I Ха2 I

Здесь ф ( а ) — средний по времени потенциал радиационной силы; Х = P _p / P ; а = c p / c ;

2/                                12/

E kin ^{( а} ) = -Pv Re ^{( а} , t ),   E pot ^{( а} ) = ---- _r p Re ^{( а} , t )

—

усредненные по времени кинетическая и потенци-, . v (а, t) + v * (а, t), .

альная энергии; vRe(а,t) =-------2-------; pRe(а,t) = p (а, t) + p * (а, t)       , ., .

=-------2-------; p(а, t) и v(а, t) — давление и колебательная скорость, определяемые из (1); звездочка и черта над функцией означают комплексное сопряжение и усреднение во времени соответственно.

ЧИСЛЕННЫЕ ПРИМЕРЫ

Рассмотрим четырехслойную камеру, описанную в работе [1], с тем отличием, что слои граничат с воздушным или жидким однородным полупространством, а также с уменьшенной толщиной первого слоя. Данные слоев представлены в табл. 1. В пятой строке в скобках представлены соответствующие величины для воздуха. В табл. 2 представлены результаты численного эксперимента для случаев системы без потерь, воздушного полупространства и жидкого полупространства со свойствами воды. Резонансные частоты рассчитывались в каждом случае тремя описанными способами,

Табл. 2. Результаты численного эксперимента

№ п/п	Система без потерь			Воздушное п/пространство			Жидкое п/пространство
	Частота резонанса F 0 , МГц	Добротность	Амплитуда волны в 3-м слое	Разность резонанс. частот, Гц	Добротность, Гц	Амплитуда волны в 3-м слое	Разность резонанс. частот, Гц	Добротность, Гц	Амплитуда волны в 3-м слое
1	2.2620	∞	∞	2.5 ∙10–5	0.72	1.32 ∙109	290.4	2365	4.4 ∙105
2	2.5564	∞	∞	2.1 ∙10–5	1.19	1.47 ∙109	255.3	4018	4.8 ∙105
3	2.8379	∞	∞	1.7 ∙10–4	6.56	1.61 ∙109	–2312	25118	4.7 ∙105

а именно: по минимуму модуля вронскиана, по выражению (18а) (кратность фазы коэффициента отражения V ₊ (0) 2 π ) и по выражениям (30), (31). Расчеты показали, что в каждом случае при резонансных частотах ∼ 2.5 МГц результаты вычислений резонансных частот разнились пренебрежимо мало, порядка 10^–4 Гц.

Под добротностью в табл. 2 понимается ширина полосы, внутри которой выполняется неравенство

1 w ( f )

≥ 0.707

1 w ( f ₀ )

где f ₀ — резонансная частота (отметим, что резонансная кривая имеет в окрестностях резонанса колоколообразный вид).

Как видно, с ростом волнового сопротивления уменьшаются добротность и значения амплитуды на резонансных частотах, растет невязка между резонансными частотами в системах с потерями и без потерь. Причем резонансная частота в полном соответствии с теорией [9] при увеличении нагрузки падает.

ВЫВОДЫ

Выше были получены выражения, связывающие геометрию и физические свойства многослойной камеры с ее резонансными частотами. В частности, варьированием геометрии примыкающего к поршню излучателя слоя жидкости можно менять входной импеданс камеры в целом и тем самым добиваться резонанса на заданной частоте. Эту частоту можно подбирать, исходя из необходимости достижения резонанса всей системы на частотах резонанса или антирезонанса виб- ратора. Подбором свойств жидкости, с которой граничит многослойная камера, можно варьировать добротность резонансной кривой камеры и коэффициент "стоячести" ("бегучести") волны в ней. В зависимости от величин этих коэффициентов можно пользоваться теми или другими выражениями для расчета радиационного давления в камере.

Таким образом, получен комплект выражений для конструирования резонансной ультразвуковой камеры и расчета радиационного давления в ней.

Работа выполнена при поддержке фонда РФФИ, грант № 05-03-33108.