О подходе к обоснованию рациональной номенклатуры эталонной базы измерительных комплексов на основе нечетких моделей

В условиях постоянного роста требований к повышению функциональности, технологично- сти, оперативности и одновременно снижению ресурсоемкости измерительных систем и комплексов, применяемых для метрологического обслуживания объектов наземной космической инфраструктуры, а также отсутствия полноценной апостериорной информации о степени реализуемости режимов и условий проведения поверочных (аттестационных) работ возникают предпосылки для поиска оригинальных подхо- дов в решении оптимизационных задач обоснования рациональной номенклатуры эталонной базы измерительных комплексов, связанных с применением теории нечётких множеств. Нечёткие оценки в ряде случаев являются единственно корректной формой отражения реальной неопределённости оценивания значений частных показателей предпочтительности того или иного варианта (состава) эталонной базы, имеющейся в распоряжении лица, принимающего решение для комплектования, например, подвижной лаборатории измерительной техники. В частности, ряд переменных, отражающих влияние внешних факторов (условий) проведения поверки (электромагнитные помехи, вибрации, солнечная радиация, состав газов и параметры их динамических состояний и т.д.) при оценивании показателя результативности поверки, а также компонент затрат на ее проведение при оценивании показателя экономичности (ресур-соёмкости) на этапе анализа вариантов формирования рационального состава эталонной базы измерительного комплекса может быть оценён лишь приблизительно, с указанием примерного интервала возможных значений и ожидаемого распределения на этом интервале.

Постановка задачи исследования

Представим множество вариантов решений по формированию рациональной номенклатуры эталонной базы отдельно взятого образца измерительного комплекса на примере подвижной лаборатории измерительной техники в виде некоторого конечного множества альтернатив

A _{ n _} = { a „..., a n }. (1)

Сравнительную предпочтительность альтернатив будем оценивать с помощью частных показателей K ₁,..., K s , s > 1. Тогда, s -мерная оценка каждой альтернативы a i ,i е {1,..., n} может быть представлена вектором

^X«s> = ⁽ x , р-^)" ⁽²⁾

При сравнении альтернатив могут возникать следующие ситуации:

• 1)    альтернатива a i не менее предпочтительна, чем альтернатива a j (a i > a j ), если X <> >X<_{s >} , т.е. x v _v > x v , v > {1,.., s };

• 2)    альтернатива a_i более предпочтительна, чем альтернатива a j ( a , >  a j ), если X <>  > X , т.е. x _v > x j _v , и хотя бы для одного v x _iv > x j _v ;

• 3)    альтернатива a i недоминируема, если не существует альтернативы a j g { a^...,a n } такой, что a j ^ a i .

Естественно, что наиболее предпочтительная среди альтернатив a ₁,..., a n относится к числу недоминируемых. Недоминируемые альтернативы образуют так называемое множество Парето [1]. При выборе наиболее предпочтительных альтернатив, как правило, недостаточно ограничиться указанием множества Парето, которому может принадлежать слишком много альтернатив. Поэтому необходимо использовать другие дополнительные методы сравнительной оценки альтернатив, связанные с построением на множестве Парето отношения предпочтения. Данные методы можно условно разделить по способу ранжирования на три группы как показано на рис. 1.

ВЕСТНИК 2017

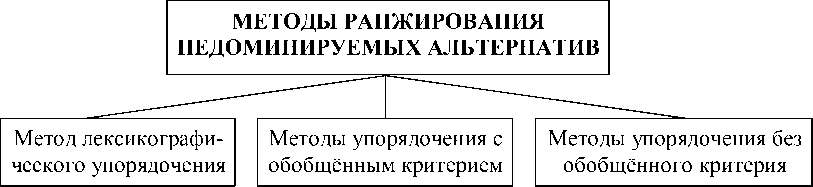
Рис. 1. Основные методы ранжирования недоминируемых альтернатив

Метод лексикографического упорядочения [2] целесообразно использовать, когда частные показатели K ₁,..., K s , характеризующие альтернативы, таковы, что их относительная важность измерима в порядковых шкалах, причем K ₁ существенно важнее всех остальных частных показателей, K ₂ - всех остальных, за исключением K ₁, и т.д.

В этом случае, если а , >  a j по K ₁, то a , >  a j независимо от оценок по остальным частным показателям K ₂,..., K s . Если же оценки альтернатив совпадают по первым r частным показателям и различаются по ( r + 1)-му частному показателю, то более предпочтительной в этом случае является альтернатива, более предпочтительная по ( r + 1)-му частному показателю.

ВЕСТНИК 2017

Легко заметить, что при лексикографическом упорядочении все альтернативы являются строго проранжированными. Одинаково предпочтительными могут оказаться лишь альтернативы с совпадающими векторами оценок. В случае лексикографического упорядочения оказывается легко решаемой задача выбора заданного числа наилучших альтернатив. Для этого достаточно выбрать нужное число первых альтернатив в их лексикографическом упорядочении.

Однако далеко не всегда частные показатели оценивания альтернатив K ₁,..., K s настолько неравноценны, настолько несоизмеримы по важности. Более типична ситуация, когда важность частных показателей является сопоставимой. В этом случае целесообразно применить различные методы свёртки - построения обобщённого критерия, либо, если обобщённый критерий нельзя построить, - методы упорядочения без обобщённого критерия.

Методы упорядочения с обобщённым критерием [3] отличаются по способам формирования обобщённого критерия. Наиболее распространены линейные обобщённые критерии, которые строятся в предположении об аддитивности, однородности частных показателей, сопоставимости их по относительной важности и независимости, как это показано в работе [4].

Предположение об аддитивности частных показателей означает, что более предпочтительной является альтернатива, у которой выше значение суммы значений частных показателей. В этом случае предполагается, что для лица, принимающего решение, существенным обстоятельством является факт суммарного превосходства альтернативы по всей совокупности рассматриваемых показателей. Однородными считаются показатели, измеряющие интенсивность свойств одной и той же природы. В случае, когда показатели таковыми не являются, их необходимо преобразовать в однородные. Сопоставимость по относительной важности для частных показателей означает, что их важность может быть сравнима с использованием количественных шкал (в отличие от порядковых при лексикографическом упорядочении).

Одним из наиболее важных предположений о характере частных показателей при использовании обобщённого критерия является предположение об их независимости.

При соблюдении указанных предположений процедура сравнительной оценки многокритериальных альтернатив сводится к построению обобщённого линейного критерия где а 1,...,as - весовые коэффициенты частных показателей K1,...,Ks, отражающие результаты сравнительной оценки частных показателей по важности.

Лучшей признаётся альтернатива a i , для которой _ss

Е ^a v ^K v ⁽ a i ) ^ E ^av^Kv ⁽ j v = 1                       v = 1

V j e {1,..., n }, j Ф i .                 ⁽⁴⁾

Если необходимо выбрать k лучших альтернатив, то ими будут k альтернатив, получивших наибольшие оценки по критерию (3).

Несмотря на достаточную наглядность критерия (3) и простоту его применения на практике, линейный обобщённый критерий не всегда может быть сформирован. В частности, при решении задач выбора вариантов построения эталонной базы измерительного комплекса некоторые показатели эффективности комплекса являются зависимыми (например, ресурсоемкость в общем случае косвенно зависит от значений показателей результативности и оперативности). Кроме того, не всегда обоснованным представляется применение в этих задачах принципа аддитивности частных показателей.

Отсутствие обобщённого критерия существенно усложняет сравнительную оценку предпочтительности многомерных альтернатив. В этом случае обычно применяются методы упорядочения без обобщённого критерия.

Одним из известных методов из этой группы является так называемый метод ЭЛЕКТРА [5]. В данном методе предлагается определять предпочтения экспертов на множестве многомерных альтернатив, не выясняя структуры и вида обобщённого критерия, а используя дополнительную функцию порогового характера о согласии и не- согласии экспертов с результирующим отноше- нием предпочтения альтернатив.

Рассмотрим произвольную пару альтернатив a_i и a_j . Обозначим класс частных показателей, согласно которым a_i не менее предпочтительна, чем а , как C ( a i , a j ), а класс, по которому действует обратное предпочтение, как D ( a i , a j ). Пусть известны коэффициенты a i ,..., a s , характеризующие относительную важность предпочтений по каждому из частных показателей. В методе ЭЛЕКТРА вводятся индекс согласия, характеризующий согласие эксперта с порядком предпочтений a i ^ a j :

c ( a i , a j ) =

s ∑ α v v = 1

∑ α v

K v e C ( a , , a j )

и индекс несогласия:

0, если D( a , a ) = 0 ;              (6)

d (a_t, a ) = ^ 1

^j    —max | x v

- x jv I

- в противном случае,

m

K v e D ( a i , a j )

где m - максимально возможная разность между оценками x v и x_jv .

Считается, что альтернатива ai предпочтительней aj, только если c (ai, aj) > c0 и d(ai, aj) < d0, где c0 и d0 - специально вводимые пороговые значения индексов (5) и (6).

Недостатком данного метода и его модификаций является эвристический характер процедур формирования классов C(ai, aj) и D(ai, aj), требующий привлечения экспертов для попарного сравнения альтернатив ai и aj, недостаточно обоснованный способ задания пороговых значений c0 и d0, а также принципиальная возможность получения вариантов упорядочений с нарушением принципа транзитивности при ранжировании альтернатив, т.е. может быть, что ai ^ aj, aj > ak и ak ^ a,.,             (7)

что, конечно, противоречит здравому смыслу при использовании метода в инженерных приложениях.

Исходя из этого, рассмотрим альтернативный метод обоснования рационального состава эталонной базы измерительного комплекса, основанный на решении оптимизационных задач.

Пусть для каждого частного показателя K v можно указать пороговое значение L_v такое, что альтернативы, оценки которых по показателю K_v ниже, чем L_v , крайне нежелательны. Более предпочтительными считаются альтернативы, оценки которых по частным показателям как можно дальше отстоят от критических значений L_v . Исходя из сущности подхода к ранжированию, данный метод можно назвать методом ранжирования по максимальному удалению от критических значений частных показателей, или, сокращённо, методом ранжирования по максимальному удалению (РМУ).

Представим математическую модель, лежащую в основе метода РМУ, в формализованном виде следующим образом.

Пусть альтернативы A = {a 1,..., an} оцениваются по s частным критериям K 1,...,Ks и X = (xi 1,...,xs) - вектор оценок альтернативы ai,iе {1,...,n}. Альтернативу ai будем считать более предпочтительной, чем aj, если min{x. -L„..., xs-Ls} > mm{ j-L„..., j-L}.

Тогда выбор наилучшей альтернативы a * осуществляется как решение задачи a * = arg max a^ € A

min J( x v — ^L v ) } v € {!,..., s }

В работе [6] показано, что задача (8) может быть решена как задача линейного программи- рования zv ^ max            (9)

i € {!,..., П }

V €{1,..., S } при ограничениях xv - Lv - ziv > 0, v g {1,...,s}, ai g A.

При небольшом числе альтернатив задача может быть решена непосредственным расчётом значений mln( x i _v - L_v ) и выбором альтернативы с максималь.ным значением данного критерия.

Обобщим правило (8) на случай, когда частные показатели Kv, v g {1,...,s} различны по важности. В данной постановке это означает, что удаление оценок альтернатив от критических значений по одним частным показателям важнее, чем по другим. Например, для одной группы эталонов важнее обеспечить более высокие значения соотношения показателей функциональной избыточности (возможности обеспечить поверку в максимально широком диапазоне воспроизводимых поверяемыми средствами измерений величин) и технологической сложности, которая косвенно отражает требования к уровню квалификации специалиста по поверке по сравнению с показателями оперативности и экономичности (ресурсоемкости) поверки. В то время как для другой важнее обеспечить более высокие значения показателей оперативной готовности и помехоустойчивости по сравнению с требованиями к точности и функциональной избыточности применяемых эталонов.

ВЕСТНИК 2017

Допустим, что определены значения весовых коэффициентов а ₁,..., a s , характеризующих важность удаления оценки альтернативы по каждому из частных показателей. Тогда задача (8) может быть записана в виде

a

= arg max a i g A

min J « v ( x iv v € {1,..., s }

- L v ) }

Соответственно, задача линейного программирования (9) принимает вид

s

z v = 1

« v z iv ^ m^ax.

i g {1,..., n }

при ограничениях xiv - Lv - ziv > 0, v g {1,...,s}, ai g A.

Или, введя функцию Ф(ai) = Z avziv, можно записать:

a * = arg max Ф( ai)(12)

ai gA xv - Lv - zv > 0, v G {1,-,s}.

Анализ составляющих выражения (12) по- зволяет выделить следующие аспекты, подлежащие уточнённому исследованию:

ВЕСТНИК 2017

• 1.    Выбор способа оценивания значений коэффициентов важности частных показателей a v , v g {1,..., s }.

• 2.    Анализ возможных способов формирования оценок x_v, i g {1,..., n }, v g {1,..., s } частных показателей.

• 3.    Исследование способов преобразования частных показателей K_v , v g {1,..., s } к однородным.

• 4.    Анализ способов задания критических значений L , , v g {1,..., s } частных показателей.

• 5.    Исследование особенностей ранжирования альтернатив с учётом возможных вариантов сочетания различных типов оценок составляющих данного выражения.

Решение

В случае если заранее можно строго проран-жировать частные показатели по важности, то можно воспользоваться следующим способом оценивания значений коэффициентов a_v .

Пусть частные показатели K_v , v g {1,..., s } представлены в проранжированном виде множеством K { s , = { K r ,..., K^r s } . Тогда можно сформировать соответствующее упорядоченное множество из коэффициентов важности ^а Г _} = { ^a i,..., a } .

Допустим, что определены значения коэффициентов сравнительной предпочтительности pij между соседними коэффициентами важности ai и aj в упорядоченном множестве a{s}, такие, a что Pij = -, j = i +1; i, j g (1,...,s}. a

С учётом этого можно составить следующую систему из ( s + 1) уравнений с s неизвестными a i :

« 1 = Р 12 ^а 2 ,

• ^а 2 = P 23 ^a 3 , .        :                                (13)

^a s - 1 = Р ( s - 1) s ^a s , s 2 a v = 1.

Решая (6), имеем:

Л                      s-1            s-1v

« s =1 1 ^{+ р} ( s - 1) s ⁺ ... ⁺ П ^P i(i + 1) ⁺ П ^p i(i + 1) I = M s ’

• V                        i =2             i=1

« s - 1 = P ( s - 1) s M s .

« s - 2 = ^P ( s - 2)( s - 1) ^P ( s - 1) s M s ,

;

a = П p».". • i=j+1

s

« 1 = П P ( - - 1) - M s i = 2

Если при строгом ранжировании частных показателей K_v по важности возникают затруднения, то можно воспользоваться методом, описанным в работе [7]. При этом предполагаются известными значения, принимаемые каждой из n ал ьт ернатив по всем частным показателям K_v , v = 1, s , т.е. векторы X =( х . 1 ,..., x . ), i g {1,..., n }. Кроме того, есть информация о парных сравнениях альтернатив, т.е. для каждой пары альтернатив a i , a j известна более предпочтительная.

Тогда задача отыскания весовых коэффициентов a_v > 0 формулируется как

Е Y ^ ^{min           (15)}

ij g I при ограничениях

Е ( x v ^- x jv ) a + Y ^ ⁰, v = 1

s

Е « v = 1, a v >  0, Y j > 0, v = 1

где I есть множество всех пар индексов i , j , для которых a i ^ a j .

Данная задача относится к классу задач линейного программирования и при сравнительно небольшом числе альтернатив может эффективно решаться с помощью ЭВМ.

Анализ возможных способов формирования оценок x i _v , i g {1,..., n }, v g {1,..., s } частных показателей показывает, что в зависимости от количества исходных данных, доступности источников информации, способов получения информации и природы частных показателей K_v оценки x_iv могут быть представлены в детерминированной, стохастической, либо нечёткой формах. Детерминированные и стохастические оценки с точки зрения формы представления выражаются в виде точечных, либо интервальных величин. Нечёткие же оценки представляют собой нечёткие множества х, i _v , определённые на множествах значений частных показателей с помощью так называемых функций принадлежности ^_iv в виде

,~ „ = { < х „ , ц „ > }, ц „ : X „ ^ [0;1].    (16)

Нечёткие оценки в ряде случаев являются единственно корректной формой отражения реальной неопределённости оценивания значений частных показателей. В частности, ряд переменных, отражающих влияние внешних факторов (условий) проведения поверки (электромагнитные помехи, вибрации, солнечная радиация, состав газов и параметры их динамических состояний и т.д.) при оценивании показателя результативности поверки, а также компонент затрат на ее проведение при оценивании показателя экономичности (ресурсоемкости) на этапе анализа вариантов формирования рационального состава эталонной базы измерительного комплекса может быть оценён лишь приблизительно, с указанием примерного интервала возможных значений и ожидаемого распределения на этом интервале.

Как уже было сказано выше, в общем случае частные показатели являются неоднородными, так как измеряют интенсивность свойств различной физической природы. В этом случае они нуждаются в преобразовании к однородным. Рекомендации, приведенные в работе [8], справедливы для случая, когда частные показатели таковы, что более предпочтительной альтернативе соответствует большее значение показателя. В противном случае преобразование показателей в однородные следует осуществлять с помощью выражений:

xV = ’   ’ = 1 - xV,(17)

xvxv

, х — xv — xv+x„ , xv - Xv xv = ---=-----= = 1 - - ~ , xv-xvx v e {1,...,s}.(18)

В большинстве практических случаев измерения значений частных показателей производятся в шкалах отношений, когда преобразование показателей к однородному виду требует знания точечных оценок x_v . Однако для некоторых частных показателей, не измеряемых в шкале [0;1], таких, например, как трудоемкость, стоимость, технологическая сложность процедуры контроля и т.п., трудно задать однозначное значение максимально возможной оценки показателя. В то же время, можно указать приближённо область значений, которой x_v принадлежит с большей или меньшей уверенностью. В этих случаях целесообразно оценивать x_v в виде нечёткой величины

X v = ^{ < ^X v , ^ v ^{( X} v ) > ^},          ⁽¹⁹⁾

где ^ ( x_v ) есть функция принадлежности нечёткого множества ~ _v максимально возможных значений оценки показателя K_v .

С учётом этого обстоятельства преобразование x _V к однородному виду производится по формулам:

~' v = Xv IXv = {< XL, Д(Xv ) >}, где xv = Xv / xv, д(xv) = д(xv);

~' ,v = ⁽ x v ^- X v ) /⁽ ~ v ^- X v ) = ^{ < ^x v , Д ^{( x} v ) > ^},⁽²¹⁾ где ^X ‘ v = ⁽ x v ^- X v ) ^{I (} x v ^- X v ), Д ^{( X}’. v ) = д ( ^X v );

~' iv = 1 - (Xv I ~ v) = {< x’v , Д(x’v) >}, где x'v =1 - (xv / xv), д(xv)=д(xv);

~' iv = ^{1 - [(} x v ^- X v ) ^{I (} ~ v ^- X v ^)] =

= {< xv, Д(x'v ) >}, где xv = 1 - [(Xv - Xv ) I (Xv - Xv )L Д(Xv ) = Д(Xv ).

Примечание . Выражения (17) и (18) получены в предположении, что минимально возможная оценка X_v по v -му показателю задана в чётком виде (обычно X_v = 0).

В формулах (17) и (18) не учитывается возможность приближённого оценивания самих значений показателей K_v . Однако, как было сказано выше (см. формулу (9)), такие ситуации могут вполне встречаться на практике. Поэтому, обобщим выражения (19) и (20), представив их с учётом нечёткого оценивания значений частного показателя K_v :

~ iv = ^{ < ^X v , Д ⁽ X v ) > ^} .

Имеем:

X' iv = X v ^{I X} v = { < 4 , Д ⁽ 4 ) > } ,     ⁽²⁴⁾

.

где X v = x v I X v , Д ( x'„ ) = supmin [ д ( X v ), д (^x_v) ] ;

v ^X iv l ^X „^{1 X} , = ^X'„ либо

X_' iv = ^{1 - ( X} v I Xv ) = { < ^X V v , Д ^{( X}' v ) > } ,    ⁽²⁵⁾

.

где

^X v = ^{1 - (} X v ^{1 X} v ), Д ^{( X} iv ) =

= supmin [ д ( X v ), д ( X v ) ] .

^x v |i - ^{( X} ,v ^{1 x} , ) = X v

Выражения для функций принадлежности ц (x' v ) в формулах (24) и (25) получены с помощью принципа обобщения Л. Заде [9].

Анализ способов задания критических значений L v , v e {1,..., s } частных показателей также показал, что наиболее корректно оценивать их значения в виде нечётких величин:

~ v = { < L v , Д ( L v ) > } .            (26)

Необходимо учитывать, что при работе с неоднородными показателями их критические значения также должны быть подвергнуты преобразованию к значению в однородной шкале:

l v = L vI X v = { < l v , д ( l v ) > } ,      (²⁷)

.

где L v = L v I x v , д ( L v ) = supmin [ д ( L v ), д ( X v ) ] ;

X v \L v I X v = X v либо

L ‘ = 1 - ( L v I X v ) = { < l v , д ( l v ) > } , (28) _.

где lv = 1 - (Lv I Xv), A(lv ) = supmin [^(Lv),^(xv)].

X v |1 - ( L v I x v ) = x v

ВЕСТНИК 2017

Сущность преобразования x v и L v к однородной шкале показана на рис. 2.

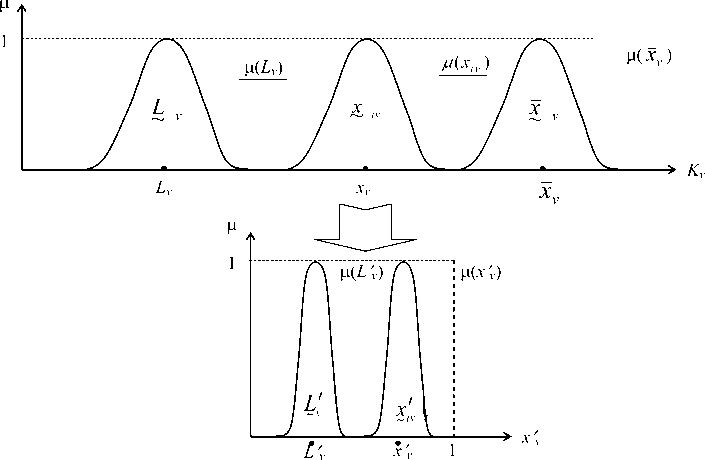
Рис. 2. Преобразование частного показателя к однородному виду

ВЕСТНИК 2017

После того как рассмотрены основные особенности оценивания частных показателей, их критических значений и способы преобразования шкал отношений к однородному виду, исследуем особенности ранжирования альтернатив по правилу (10).

С учётом проведённого анализа в наиболее общей постановке задача выбора наилучшей альтернативы описывается выражением:

a * = arg max[ min ^{ a _v ⁽ x „ - L ' _v ^)}],    ⁽²⁹⁾

ai G a vе{1,...,5} где ~ iv есть результат приближённого оценивания i-й альтернативы по v-му частному показателю, преобразованному к однородному виду.

Очевидно, что результатом преобразования а (x - L- L ’ ) будет нечёткое множество А. v ^~ iv ^~ v                                                  ^~ iv взвешенного нормированного расстояния (удаления) оценки i-й альтернативы по v-му частному показателю от критического значения:

~ iv = { < s „ , Ц^ ) > } ,         (30)

где S v = ^a v ⁽ x i v ^- L ) = ^a v ⁽ 4 / x v ^- L v / x v ) , либо S _iv = ( L_v / x_v - x_v I x_v ) - в случае, когда лучшей альтернативе соответствует меньшее значение показателя. Функция принадлежности ц ( S iv) соответственно оценивается выражениями:

p ( S ,v ) = sup min [ ц ( x ' v ), ц ( l v ) ] ,    (31)

s iv а f x iv - L ^ ] = s v либо                 I ^ x^v x^v ^

^ ^{( s} v ) = sup^min [ Ц ⁽ x ' v ), ^ ⁽ L v ) ] . ⁽³²⁾ s iv^,:л f LT - x v P *

С учётом (31), задача (32) может быть записана в виде:

а * = argmax[ min А _iv ]. (33) a i _e a v e ^{1,..., ^{5 }} ~

Таким образом, задача выбора рационального варианта сводится к задаче поиска минимальной нечёткой оценки удаления каждой альтернативы от критического значения по всем частным показателям и, затем, выбора среди таких альтернатив наилучшей по максимальному удалению.

Для ранжирования нечётких множеств можно воспользоваться одним из известных методов, описанных в литературе, например методом сравнения нечётких подмножеств единичного интервала [10]. Согласно этому методу, сравнение нечётких множеств может производиться на основе так называемой функции упорядоченности, представляющей собой скалярное число из единичного интервала.

Пусть ~ A - нечёткое подмножество единичного интервала A = { < x , ц ( x ) > }, x е [0;1]. Определим уровневое множе с тво как

Aa = {x I ЦA (x)} ^ а, ~ где а есть некоторый заданный уровень, 0 < а < 1. Пусть а(а) и b(а) есть соответственно левая и правая границы множества Аа. Определим функцию M(а) как среднюю величину интервала [а(а), b(а)], т.е.

M ( а ) =

а ( а ) + b ( а ) 2

.

Тогда, функция упорядоченности F ( ~ A ) может быть рассчитана как

a.

α max

∫ M ( α ) d α

F ( ~ A ) = ⁰ _J ,         (34)

где J = 1/ dα .

При практических расчётах задаются некоторым интервалом дискретизации dα множества значений α , так что оно разбивается на конечное число непересекающихся интервалов: 0 <  α ≤ dα , dα < α ≤ 2 d α,…, 1 – dα < α ≤ 1.

Для каждого j -го интервала находится значение M _j ( α ), затем рассчитывается приближённое значение F ( A ):        J

~       ∑ M j ( α )

F ( ~ A ) ≈ ^{j = 1} _J .            (35)

Таким образом, по функции упорядоченности можно проранжировать нечёткие множества Δ и Δ , что позволяет выбрать наиболее ~ iv    ~ imin предпочтительную альтернативу a*, то есть определить рациональную номенклатуру эталонной базы измерительного комплекса (ПЛИТ).