О подобии поляризационно-оптических откликов магнитных наножидкостей. Ч. I. Аппроксимация для слабых полей

Знание особенностей распространения лазерного излучения через измерительную систему с находящимися в ней исследуемыми объектами позволяет регистрировать их структурные изменения, важные для многих приложений [1–13]. В этой связи особый интерес представляет применение количественных методов лазерного поляризационно-оптического анализа к исследованию поляризационных откликов, которые появляются в результате какого-либо воздействия на вещество или материал. Такое воздействие может возникать, например, в результате крепления образца (оптического элемента), наложения внешнего, в частности, магнитного поля и по другим причинам [3, 12, 14–16]. Для более полного понимания и последующего применения результатов подобных исследований необходимо развивать подходы и методы, позволяющие количественно оценивать характер наблюдаемых зависимостей. Данная работа посвящена развитию основ методики количественной характеризации слабых поляризационных откликов магнитных наножидкостей [14, 17, 18].

АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ И ОЦЕНКА ПОДОБИЯ

ПОЛЯРИЗАЦИОННЫХ ОТКЛИКОВ

Следуя работе [17], будем аппроксимировать экспериментальные зависимости величины отклика магнитных наножидкостей от магнитного поля полиномом второй степени. Предположим, что отклик измерен в N точках от i = 1 до i = N , причем каждое измеренное значение отклика y ( i ) соответствует определенному значению магнитного поля H ( i ) :

y ( i ) = к 2 • H ( i )² + к , • H ( i ) + k 0 .          (1)

Табл. 1. Номера экспериментов с разными концентрациями магнитных НЖ

Характеристика	Номер эксперимента
	1	2	3	4	5	6	7	8	9
Концентрация магнитной НЖ в %	1	1	0.2	0.04	0.01	0.003	0.001	0.0001	0.0001

Табл. 2. Значения коэффициентов квадратичной зависимости для каждого эксперимента

Номер эксперимента	Коэффициент k 2	Коэффициент k 1	Коэффициент k 0
1	0.000332	0.009830	–0.014274
2	0.000323	0.010286	–0.016859
3	0.000356	0.009086	–0.029623
4	0.000269	0.014139	–0.044834
5	0.000344	0.009158	–0.012889
6	0.000322	0.009964	–0.010816
7	0.000342	0.008901	0.021204
8	–0.000151	0.032268	–0.070467
9	–0.000124	0.028847	–0.070467

Индексы коэффициентов k соответствуют степеням членов полинома. Проведем теперь количественное сравнение отклонений аппроксимирующих полиномов для результатов экспериментов с наножидкостями (НЖ) различных концентраций. При этом будем использовать экспериментальные данные, полученные в работе [14] для НЖ из наночастиц магнетита в керосине. Значения концентрации НЖ и соответствующие номера экспериментов представлены в табл. 1.

Значения коэффициентов k для каждого эксперимента представлены в табл. 2.

Для проведения сравнений степеней аппроксимирующих полиномов проведем вычисление евклидовых расстояний между аппроксимирующими полиномами и экспериментальными данными. Евклидовы расстояния, или, иначе говоря, евклидовы нормы вычисляются по следующей формуле:

norm =

N

Z (Y i - y^¹.

i = 1

В этой формуле N — количество экспериментальных данных; y_i — i -е значение результата измерения, соответствующее i -му значению магнитного поля; Y_i — i -е значение аппроксимирующего полинома, соответствующее i -му значению магнитного поля.

В табл. 3 приведены результаты вычисления норм отклонений от аппроксимирующих полиномов различных степеней, соответствующих экспериментам 1–9.

Как видно из таблицы значение средних квадратичных отклонений измеренных данных для экспериментов 1–3, 5, 6 не превышают 10 %, для экспериментов 4, 7 не превышают 20 %, а для экс-

Табл. 3. Значения норм отклонений результатов измерений от аппроксимирующих полиномов различных степеней, соответствующих экспериментам 1–9

Номер эксперимента Значение нормы по формуле (2) для полинома второй степени 1 0.0823 2 0.0840 3 0.0702 4 0.1680 5 0.0746 6 0.0653 7 0.1786 8 0.4387 9 0.4361 периментов 8 и 9 составляют примерно 43 %.

В Приложении на рис. 1 представлен график результатов экспериментов с 1 по 6 усредненного полинома 2-й степени.

Там же на рис. 2 представлены графики функций плотностей вероятностей отклонений экспериментальных данных от усредненного полинома для экспериментов 1–6. Перед вычислением отклонений от усредненного полинома из всех экспериментальных данных была вычтена постоянная составляющая. В качестве постоянной составляющей использовалось среднее значение коэффициента k ₀ , представленного в табл. 1.

В Приложении на рис. 3 представлены графики функций плотностей вероятностей отклонений экспериментальных данных от усредненного полинома для экспериментов 7–9.

Вычисленные значения отклонений экспериментальных данных от усредненного полинома были проверены по критерию Колмогорова— Смирнова (Kolmogorov-Smirnov test) на принадлежность плотности вероятности к распределению Гаусса. Проверка показала, что гипотеза о принадлежности этих отклонений к распределению Гаусса подтвердилась для всех экспериментов, кроме эксперимента 9.

Различие математических ожиданий полученных плотностей вероятностей отклонений от усредненного квадратичного полинома проверялось по t -критерию Стьюдента [19, 20].

Этот тест предназначен для проверки нулевой гипотезы, предполагающей, что выборки X и Y получены из генеральных совокупностей, имеющих одинаковое среднее значение. Число элементов в векторах X и Y было одинаковым и равнялось 42.

Проверка нулевой гипотезы выполнялась на основе статистики t :

t = x x,^ ,                   (3)

s ² s ²

n ₁ n ₂

где x , и X , _{+ 1} — значения математических ожиданий в соседних пиках функций плотности вероятности; n ₁ и n ₂ — количество чисел, соответствующих соседним пикам функций плотности вероятности; s — случайная ошибка измерений. Для всех экспериментов s оказалась практически одинаковой. Далее задаем желаемую вероятность правильного вывода P и по ней находим соответствующее значение t ( P ) с помощью функции t = t ( P ), которая является обратной для функции P = 2Ф( t ), где Ф( t ) — интеграл вероятности [20]. Например, при P = 0.99 значение t ( P ) = 2.576. Если абсолютная величина отношения (3) не превосходит соответствующее значение t ( P ) , то расхождение математических ожиданий можно считать случайным с надежностью вывода P . В противном случае есть основание считать расхождение неслучайным (значимым).

Статистическая гипотеза о равенстве математических ожиданий отклонений экспериментальных данных от усредненного полинома второй степени подтверждается для всех экспериментов, кроме 9-го, со стандартным уровнем значимости (significance level) 5 %. Данная гипотеза подтверждается для указанных экспериментов только для данных, из которых вычтена постоянная составляющая.

ВЫВОДЫ

• 1.    По статистическому t -критерию Стьюдента гипотеза о равенстве математических ожиданий отклонений экспериментальных данных опытов с разной концентрацией от 1 % до 0.003 % от квадратичных кривых подтверждается со стандартным уровнем значимости (significance level) 5 % при условии вычитания из экспериментальных данных постоянной составляющей.

• 2.    Сравнение норм отклонений опытов с малой концентрацией с нормами опытов с концентрацией, равной 1 %, показало, что эти нормы отличаются не более чем на 22 %, а для некоторых опытов отличие норм отклонений составило менее 11 %.

• 3.    Сравнение коэффициентов при второй степени аппроксимирующего полинома для опытов с разной концентрацией показало, что эти коэффициенты отличаются не более чем на 18 %, а для ряда экспериментов это отличие составило менее 10 %.

• 4.    Функции плотностей вероятностей отклонений экспериментальных данных от усредненного полинома для измерений в экспериментах с концентрациями от 1 % до 0.003 % имеют распределение Гаусса.

• 5.    В диапазоне изменения объемных концентраций магнитных наночастиц от 1 % до 0.003 % экспериментальные зависимости величины поляризационных магнитооптических откликов от магнитного поля, представленные в работе [14], являются подобными.

Работа поддержана РФФИ: проект 15-02-08703.

ПРИЛОЖЕНИЕ

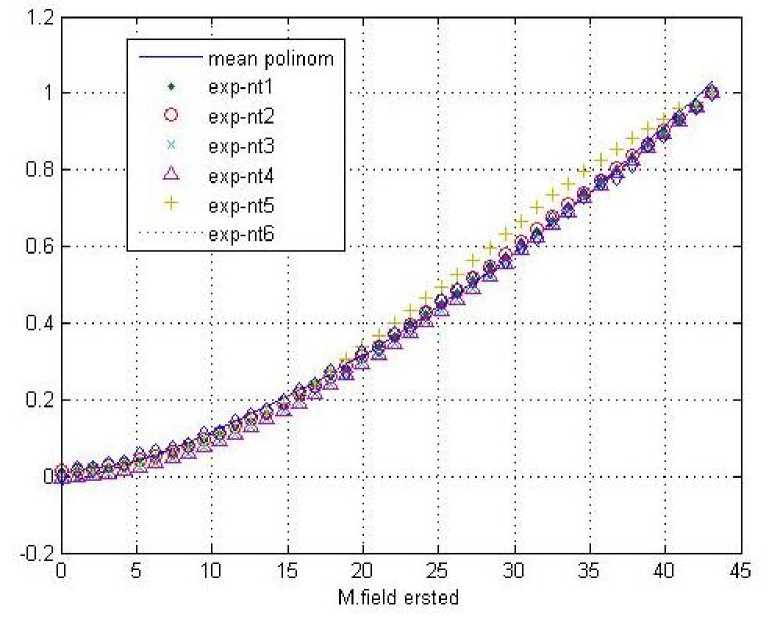
Рис. 1. Усредненный полином и результаты экспериментов с 1 по 6

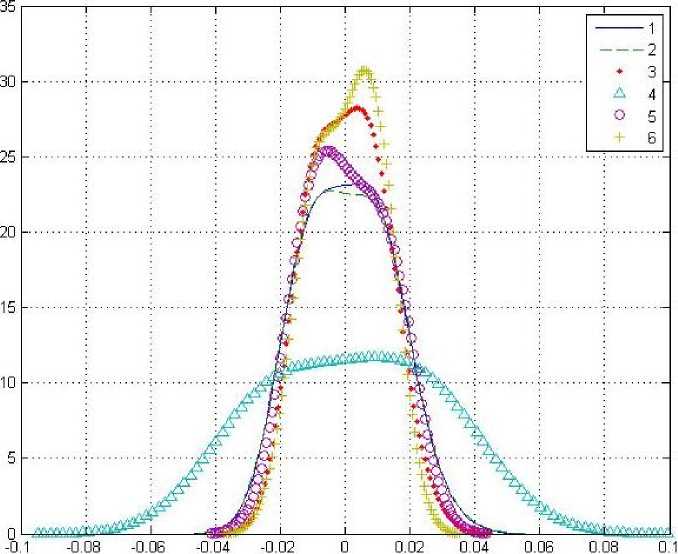
Рис. 2. Графики функций плотностей вероятностей отклонений экспериментальных данных от усредненного полинома для измерений в экспериментах 1–6

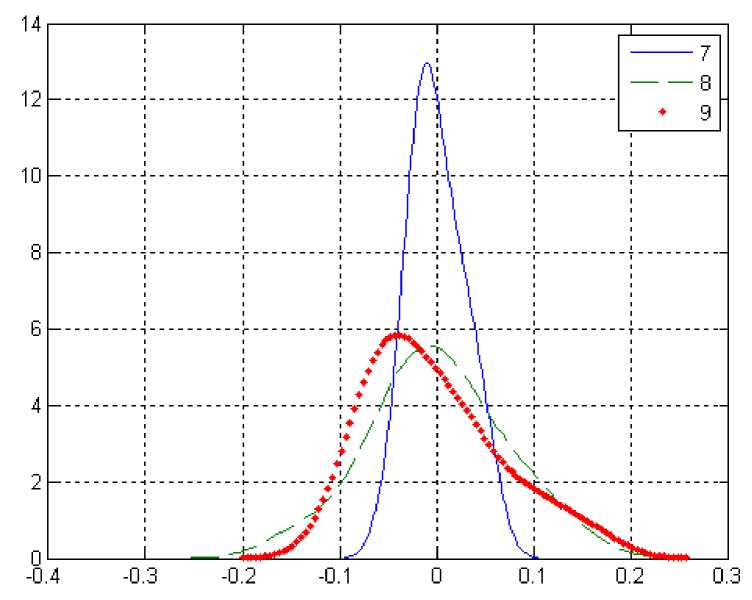
Рис. 3. Графики функций плотностей вероятностей отклонений экспериментальных данных от усредненного полинома для измерений в экспериментах 7–9