О показателе степени некоторых числовых равенств

Теорема : Верное числовое равенство вида:

f ( Ак ) п = В"                               (1)

к =1

где:  Ак , В – целые, положительные, взаимно простые основания степеней слагаемых

⁽ Ак ) "

и суммы ( В )

;

n > 1 – натуральный показатель степени, существует при n = R, где: R – количество слагаемых в числовом равенстве.

Доказательство:

Пусть существуют удовлетворяющие условиям теоремы основания степеней

Ак , В для которых числовое равенство (1) верно. Представим каждое из входящих в числовое равенство слагаемое (Ак) и сумму (В) в виде тождеств, являющихся биномами Ньютона при натуральном показателе степени n:

п

( Ак ) п = ( Хк + ( Ак - Хк )) п = f ( " ) ( Хк ) i ( Ак - Хк ) п i i =0 i

п

В = (У + ( В - У)) = f ( " ) У i ( В - У )                            (2)

i=0 i где: Хк, У – могут принимать любые значения, то есть, являются переменными.

Подставляя тождества (2) в числовое равенство (1), получим алгебраическое уравнение:

f f ( " ) ( Хк ) i ( Ак - Хк ) п - i = f ( " ) ( У ) i ( В - У ) п - i                       (3)

к =1 i =0 i                                                   i =0 i

Поменяв местами символы сумм, и вынеся коэффициенты ⁽ - | за символ k i )

суммы независящий от значений n и i, что равнозначно перестановке мест слагаемых в уравнении (3), получим:

^ ( - )[ ]f ( ^хк ){ Ак - Хк ) • -' ] = ff ( - ][ У ( В - У ) n -' ]                   (4)

= 0        L k = 1                                       J i = 0

Алгебраическое уравнение (4) соответствует числовому равенству (1) и справедливо при любых значениях переменных Хк, У, входящих в это уравнение.

Лемма.

Если существует верное числовое равенство (1), где:

Ак ,В - целые, положительные, основания степеней слагаемых (Ак) и суммы (В) , n > 1 – натуральный показатель степени, то в соответствующем ему алгебраическом уравнении (4) для любого значения переменной У можно найти такие значения переменных Хк, при которых будут равны между собой все соответствующие слагаемые обеих частей этого равенства.

Доказательство леммы:

Пусть существует удовлетворяющее условиям леммы верное числовое равенство (1), а следовательно и соответствующее ему алгебраическое уравнение (4).

Пусть утверждение леммы верно и в алгебраическом уравнении (4) можно найти такие переменные Хк, У, для которых выполняется система уравнений, состоящая из (n + 1) уравнения:

R

Е ( Ак - Хк) п = (В-У) п к=1

Е (Хк) ( Ак - Хк) п-1=У (В-У) п-1 к=1

]    Е (Хк )2( Ак - Хк) п-2 = У 2( В-У) п-2             (5)

к =1

……………………………………………

R

I  Е (Хк)"=У к =1

Следует отметить, что система уравнений (5) существует для числового равенства (1) только в том случае, если основания Ак , В являются целыми числами. Если, например, число В иррациональное (при этом число В n является числом целым по условию), то при показателе степени n > 1 можно подобрать целые переменные Хк, У такими, что все левые части системы уравнений (5) будут целыми, в то время как в правой части часть уравнений будет иметь иррациональные значения, что является противоречием.

Аналогично система уравнений (5) может не существовать и для числовых равенств типа (1) если основаниями степеней являются рациональные дроби.

Пусть основания Ак , В целые, положительные числа. Для таких числовых равенств существует система уравнений (5). Система уравнений при помощи тождественных преобразований приводится к виду (преобразование системы уравнений приведено в приложении 1):

t ( Ак ) п = В к =1

■■ Ак )п6

Вп

' у ^

R

t (Ак)

к =1

п ^ ^Хк Y V Ак )

= В

IВ)

(Хк '■V Ак

=В

V в ;

Следовательно,

если существуют удовлетворяющие условиям леммы основания степеней Ак , В для которых числовое равенство (1) верное, то существуют соответствующая ему система уравнений (5) и преобразованная система уравнений (6).

По условию показатель степени n входящих в равенство слагаемых ( Ак) и суммы Вn больше 1. Тогда количество уравнений в системе уравнений (6) не меньше 3.

Умножая первое уравнение полученной системы на множитель (У/В)2, а второе на (-2У/В), и складывая первые три равенства, получим:

R

Z (Ак)

к =1

■ fУ IВ

Хк Y ----  = 0

Ак _v

Следовательно, если существуют такие целые основания степеней Ак и В , для которых числовое равенство (1) верно при n > 1, то существует соответствующее этому числовому равенству алгебраическое уравнение (7).

По условию леммы основания Ак , В , а следовательно и слагаемые ( Ак) , являются положительными числами. Тогда для выполнения равенства (7), (поскольку квадрат множителя в скобках при любых значениях входящих в него переменных не отрицателен), необходимо выполнение условий:

ХкУ

АкВ где индекс к пробегает значения от 1 до R (R – количество слагаемых в числовом равенстве (1)).

Или в виде системы уравнений:

Х1

А1

Х 2

А 2

X r = У .

АR

Полученные условия преобразования (9) содержат R уравнений (где R – количество слагаемых равенства (1)) и устанавливают при заданных целых, положительных основаниях Ак , В соотношения между переменными уравнения (4), при которых любому значению одной из переменных У или Хк можно найти такие значения остальных переменных, при которых будут равны между собой все соответствующие слагаемые обеих частей уравнения (4) (в этом можно убедиться, подставив полученные соотношения (9) в равенство (4)).

Таким образом, если числовое равенство (1) верное, положительные основания степеней Ак

и В слагаемых

(Ак )'

и

суммы ( В )

являются

целыми числами, а натуральный показатель степени n > 1, то существует соответствующее ему тождественно преобразованное алгебраическое уравнение (4) и условия его преобразования (9), позволяющие преобразовать одну часть уравнения (4) к виду его другой части. Условия преобразования (9) из всей совокупности верных и неверных числовых равенств типа (1) при показателе степени n > 1 выделяют верные числовые равенства и, если эти условия не выполняются, то не существует и верного числового равенства (1).

Очевидно, что уравнения, входящие в систему уравнений (9), имеют нетривиальные (отличные от ноля) решения (все уравнения системы являются линейными, а одной из переменных можно задавать любое значение).

Следовательно, верное числовое равенство типа (1) при выполнении условий леммы можно преобразовать к виду (4), где каждое из слагаемых правой части будет равно сумме соответствующих слагаемых левой части.

Лемма доказана.

Полученная система уравнений (9) имеет однозначные решения только в том случае, если хотя бы одно из оснований слагаемых или суммы не может быть представлено в виде другого целого основания с некоторым натуральным показателем степени отличным от 1.

Если все основания числового равенства (1) можно представить в виде некоторых целых положительных чисел с отличным от 1 натуральным показателем степени, то, выбрав какое либо из уравнений системы (9) (для примера взято первое уравнение), будем иметь:

В=в t=У А"

Х 1

Откуда получаем для нового основания в:

в

= ± t

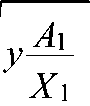
Полученное значение основания в имеет как положительные, так и отрицательные значения (их количество равно t), что противоречит условию теоремы. По условию теоремы оно должно иметь положительное значение.

Если все основания числового равенства можно представить в виде некоторых целых чисел с отличным от 1 показателем степени, то это говорит о неверности выбора показателя степени всего числового равенства (1). В этом случае в системе уравнений (9) решения каждого уравнения будут иметь неоднозначные, отличающиеся знаком, значения, противоречащие исходному числовому равенству.

Только если показатель степени t хотя бы одного из входящих в числовое равенство оснований равен 1, то все уравнения системы (9) становятся однозначными (Они путем перестановок приводятся к виду, когда в каждом уравнении будет однозначное значение основания в).

Числовые равенства типа (1), удовлетворяющие условиям теоремы, удовлетворяют и условиям леммы. Для таких равенств существует тождественно преобразованное алгебраическое уравнение (4) и соответствующие ему условия преобразования (9) определяющие его верность. Следовательно, для удовлетворяющих условиям теоремы верных числовых равенств типа (1), существует система уравнений:

f  L(")[L(Xk)i(Ак-Хк)'"i]=L(n)[уi(В-У)'-i]

i = 0          k = 1                                                 = 0

Х1 УА1 В

Х2 УА2 В

ХR УАR В

Или, что тоже самое:

f (Ак) ’ = В к =1

Х1

А1

Х2

А 2

ХR

АR

По условию теоремы все основания степеней Ак , В являются взаимно простыми числами, а следовательно в системе уравнений (10) нет сократимых и одинаковых уравнений при любой их перестановке.

Полученная система уравнений приводится к виду системы уравнений (6):

R

£ (Ак) п = В"

к =1

R

Z (Ак)

к =1

Хт' V Ак J

= В "

' У

R

Z ( Ак ) " к =1

V Ак )

= В

п

IВ )

R

Z (Ак)

к =1

" ( ^Хк У V Ак J

= В

V В )

Она отличается от системы уравнений (6) только количеством уравнений в системе. В системе уравнений (6) количество уравнений равно (n + 1), а в системе уравнений (11) оно равно (R + 1), где R – количество слагаемых числового равенства (1).

Система уравнений (11) очевидно является равносильной системе уравнений (6) (системы уравнений имеют одни и те же решения и относятся к одному и тому же числовому равенству).

Система уравнений (11) при помощи тождественных преобразований аналогичных преобразованиям приложения № 1, но в обратном порядке (свертка системы уравнений (11)), приводится к равенству типа (1) только в том случае, если показатель степени n = R (где R – количество слагаемых в равенстве (1)).

Следовательно, если существует удовлетворяющее условиям теоремы верное числовое равенство типа (1) с показателем степени n >  1, то его показатель степени n = R, что и требовалось доказать.

Теорема нарушается, если среди оснований Ак , В имеются сократимые числа.

Чтобы показать это, предположим, что существует числовое равенство:

£ ( Ак ) " - В к -1

в котором основания степени А и В являются сократимыми. Запишем их в виде:                 Ar - NT

В - NP где: P и T – целые, несократимые числа, N – общий множитель.

Тогда числовое равенство примет вид:

£ (Ак) п+(NT) n - (NP) п(12)

к -1

После проведения операций 3 – 8 получим для условий преобразования систему уравнений аналогичную системе уравнений (9):

Х1

A i NP

Х 2

А 2 NP

Х R -1 ₌ У

Ar-1 NP JC^ - У NТ NР

А соответствующая числовому равенству система уравнений (аналогичная системе уравнений (10)) примет вид:

(    t (Ак) п+(NT )n = (NP) п к =1

• Х 1 У

• Ai NP

Х 2 = У- •                     (14)

• <         А 2 NP

X r -1 , У

A r -1   NP

ХR  УNТ NР

Последнее уравнение в полученной системе уравнений является сократимым, что и приведет к нарушению теоремы.

Свертка системы уравнений (14) соответствует числовому равенству (12), а свертка этой же системы уравнений после сокращения последнего уравнения невозможна без умножения на множитель (последнее уравнение относится к иному числовому равенству). Для исключения этой неоднозначности необходимо рассматривать подобные исходные числовые равенства (12) первоначально разделив их на множитель N:

R-1( Ак Л n xn t       +(T) = (P)п                    (15)

к=1 v N 7

Полученное числовое равенство (15) содержит в своем составе как целые основания степеней, так и рациональные дроби, что выходит за рамки теоремы (нарушается требование целостности оснований числового равенства (1)), может привести к нарушению леммы (невозможности представления в виде системы уравнений (5) аналогично наличию среди оснований иррациональных чисел) и соответственно нарушению теоремы.

Выводы из теоремы:

Согласно теореме числовые равенства типа (1), удовлетворяющие условиям теоремы, имеют показатель степени n = R (где: R - количество слагаемых в равенстве). Теорема может быть нарушена если среди оснований Ак ^, В имеются сократимые числа.

Исключение составляют числовые равенства имеющие в своем составе только два слагаемых. Такие числовые равенства при отсутствии иррациональных оснований всегда приводимы к условиям теоремы (доказательство приведено в приложении 2).

Следовательно, натуральный показатель степени числовых равенств типа (1) при отсутствии иррациональных оснований и количестве слагаемых R = 2 не может быть больше 2 (большая теорема Ферма).

P.S.: Приведенная выше теорема является частью более общей теоремы. Аналогично можно доказать, что верное числовое равенство вида:

RN

Z ( Ак ) п - Z ( Bt ) п к =1                     t =1

где: Ак, Вt – целые, положительные, взаимно простые, основания степеней слагаемых (Ак)n и суммы (Вt)n;

n > 1 – натуральный показатель степени, существует при n = (R + N – 1), где: R и N – количество слагаемых соответственно в левой и правой частях равенства.

Доказательство ничем не отличается от приведенного выше, за исключением применения необходимого количества операций аналогичной операции перехода из системы уравнений (6) к уравнению (7) (эта операция позволяет поочередно исключать слагаемые из одной части равенства) и далее получения условий аналогичных условию (8).

Приложение 1.

Пусть имеем систему уравнений (5):

£ (Ак - Хк) " = (В-У) "

к =1

£ (Хк) (Ак-Хк)'-1 = У (В-У)'-1 к=1

£ (Хк )2( Ак - Хк) п-2 = У 2( В-У) п-2 к=1

R

£ (Хк) " = У к=1

Вынеся множители ( Ак ) и В" за скобки, преобразуем ее к виду:

R

£(Ак)

к =1

• [ Хк 1 V Ак ;

= В"

I в J

R

£ ( Ак ) п к =1

1-^VАк) V Ак)

= В "

V В ) V ^{1 -} В J

R

£ ( Ак ) " к =1

f Хк ) f

V Ак ; V

X 2

Хк 1

Ак )

= В

п

^f У 1 " Т- У 1

V в ) V в J

R

£ ( Ак ) п 1

к =1

Хк 1 = В"f 1-У ' Ак J V в ;

Каждое уравнение системы является комбинацией всех предшествующих ему в этой системе уравнений. Для исключения из какого либо i-го уравнения системы всех предшествующих ему уравнений этой же системы, необходимо предшествующие ему уравнения до i-го включительно умножить на коэффициенты бинома Ньютона соответствующие показателю степени i и произвести свертку полученных таким образом уравнений. Тогда, после свертки этих уравнений для i-го уравнения системы получим:

£ ( Ак ) " к =1

f Хк) f ХкVАкJ VАк

Ак J

= В

V в J V в в J

Или окончательно i-ое уравнение системы будет иметь вид:

£ ( Ак )

к =1

f Хк у Ак J

= В п

V В J

Проделав аналогичные операции по разделению уравнений с каждым из уравнений системы, получим систему уравнений аналогичную системе уравнений (6):

R

£ ( Ак )" = В " к =1

R

Z (Ак)

к =1

f Хк У V Ак J

= В

п

R

£ (Ак)

к =1

" f Хк А 2

f S

V Ак J

= В

п

V В J

R

Z (Ак)

к =1

" ( ^Хк У V Ак J

= В

V В J

Следует отметить что все проделанные операции являются тождественными преобразованиями, а следовательно они обратимы. Это означает, что если существует система уравнений (6), то, произведя свертку этой системы (действия аналогичные приведенным преобразованиям, но в обратном порядке), получим исходное числовое равенство.

Приложение 2.

Пусть существует числовое равенство:

' A ) +^f C 1 -^f E '

n

V B J

VD J

VF J

где: A, B, C, D, E, F – целые числа.

Это числовое равенство путем приведения к общему знаменателю приводится к виду числового равенства с целыми основаниями:

( ADF ) n+( BCF ) n=( BDE ) n            (16)

В полученном числовом равенстве слагаемые имеют общий множитель F. Представим полученное числовое равенство в виде:

( AD) n+( ВС) n-f BDE I n

• V F J

Левая часть числового равенства представляет собой целые числа. Следовательно и правая часть также является целым числом. Это означает, что частное от деления произведения (BDE) на целое число F также является числом целым. Следовательно, числовое равенство (16) сократимо. После деления обеих частей равенства на целое число Fⁿ , получим числовое равенство удовлетворяющее условиям приведенной выше теореме.