О последовательном построении непараметрических оценок регрессии

Введение. Широкое распространение методов моделирования, идентификации объясняется возможностью их применения для построения моделей явлений, объектов и процессов разной физической природы. Универсальность и эффективность методов идентификации позволяют применять их как для различных технических систем (в том числе и в ракетнокосмической отрасли), так и в медицине, экономике и других областях науки и практики.

На сегодняшний день существует широкий спектр методов идентификации: от традиционных методов статистического анализа до современных алгоритмов машинного обучения [1]. В последние годы большую популярность получило построение коллективов моделей (ансамблей) [2–4].

Одной из основных задач объединения нескольких моделей одного типа является устранение тех или иных недостатков определенных моделей. Например, если деревья классификации и регрессии (CaRT) [5] склонны к переобучению, то их коллективы (Random Forest [6], GBM [7; 8]) менее подвержены этому негативному эффекту.

В данной работе предложен подход к формированию ансамбля непараметрических оценок Надарая– Ватсона [9], позволяющий получать более гладкие и точные оценки в разреженных подобластях пространства входных переменных, чем при построении единственной непараметрической оценки.

Постановка задачи. Формально задачу идентификации можно записать следующим образом [10]. Имеется множество наблюдений:

G = ^{ g 1 , g 2 , ..., g n ^{} .}

Каждое наблюдение характеризуется набором переменных:

gi ={xn xh -,xm, y,}, где x1, x2, …, xm – независимые переменные, значения которых известны и на основании которых определяется значение зависимой переменной y. Требуется восстановить зависимость между независимыми входными переменными x1, x2, …, xm и выходной переменной y. Какая-либо другая априорная информация об исследуемом объекте отсутствует.

При подобных постановках задачи одним из распространенных методов [11–13] восстановления зави- симости между входом и выходом является непараметрическая оценка регрессии Надарая–Ватсона:

^{y (} x ) =

nm znK i=1 j=1

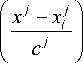
yi

где K – ядерная функция; ͞ с – вектор параметров размытости.

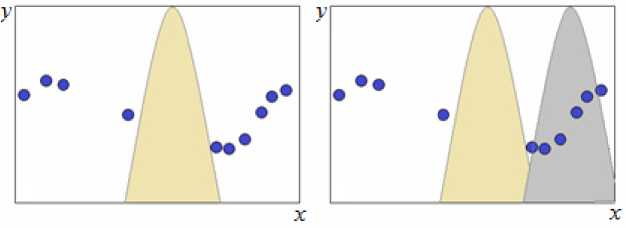
Однако в ряде случаев данный подход имеет некоторые недостатки. При наличии разреженных областей в пространстве входных переменных (рис. 1) минимальный параметр размытости (рис. 1, а ), необходимый для того, чтобы оценка (1) существовала во всех точках исследуемой области пространства входной переменной, настолько велик, что в некоторых точках ядро захватывает большую часть наблюдений (рис. 1, б ), что может привести к определенным искажениям оценки.

Другой важный момент связан с уменьшением точности оценки (1) на границах пространства входных переменных [14].

Данные недостатки могут быть устранены с помощью объединения непараметрических оценок Надарая–Ватсона в ансамбль последовательного обучения [15].

Ансамбль непараметрических оценок. Идея построения ансамбля непараметрических оценок состоит в итеративном улучшении некоторой начальной (базовой) оценки регрессии Надарая–Ватсона за счет последовательного добавления непараметрических оценок невязок текущего ансамбля.

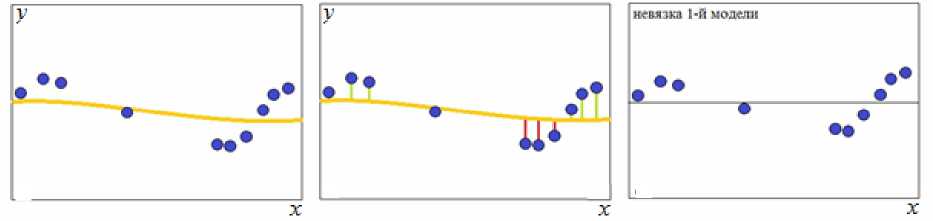
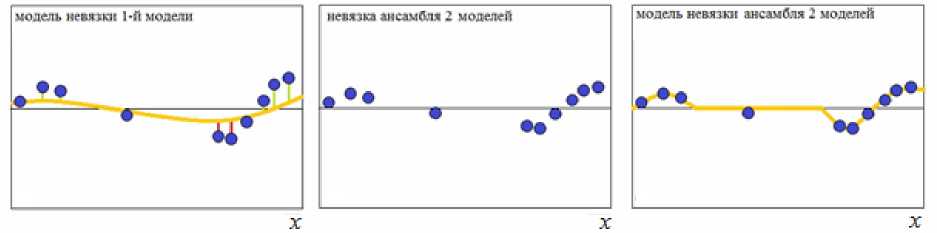
Процедура формирования ансамбля показана на рис. 2. Процедура начинается с построения некоторой базовой оценки (1) с большими параметрами размытости. Затем вычисляются невязки между выходом объекта и выходом базовой оценки, по которым строится следующая непараметрическая оценка (1) с меньшими параметрами размытости. Данная оценка добавляется к базовой оценке, так формируется ансамбль первого уровня. Затем вычисляются невязки между выходом объекта и выходом ансамбля первого уровня, и так далее, пока добавление каждой новой оценки в ансамбль приводит к его улучшению.

а

б

Рис. 1. Ядро минимальной ширины:

а – позволяющее получать некоторое значение оценки (1) в любой точке исследуемой области пространства входной переменной; б – захватывающее более половины наблюдений

а                                      б                                 в

г                                           д                                      е

Рис. 2. Процедура формирования ансамбля непараметрических оценок последовательного обучения: а - построение базовой оценки с большим параметром размытости; б - вычисление невязок между выходами объекта и модели; в - формирование выборки, состоящей из невязок; г - построение модели невязки с меньшим параметром размытости, вычисление невязки ансамбля первого уровня; д - формирование выборки, состоящей из невязок ансамбля первого уровня; е - построение модели невязок ансамбля первого уровня с меньшим параметром размытости

На первых итерациях (при больших параметрах размытости) алгоритм восстанавливает зависимость в разреженных областях, при этом оценки в областях с достаточным количеством наблюдений, очевидно, уступают в точности непараметрической оценке, построенной с меньшими параметрами размытости. Начиная с некоторого шага, ядро непараметрической оценки в точках разреженных областей перестает захватывать какие-либо из имеющихся наблюдений, процесс формирования ансамбля для таких областей автоматически прекращается. Одновременно с этим начинается уточнение оценки в областях с достаточным количеством наблюдений. Таким образом, предлагаемый алгоритм позволяет строить максимально точные (из возможных в классе непараметрических оценок Надарая-Ватсона) оценки как в разреженных областях пространства входных переменных, так и в областях, в которых количество наблюдений велико.

Формирование ансамбля непараметрических оценок регрессии. Формирование ансамбля непараметрических оценок Надарая-Ватсона происходит последовательно. Каждая последующая оценка добавляется в ансамбль с целью улучшить его качество. Данный процесс продолжается до того момента, пока уменьшается значение меры рассогласования L выхо да модели (ансамбля) и объекта, вычисленное по ва-лидационной выборке (х, у):

L ( H q ( X ) , у ) < L ( H q - , ( X ) , у ) .

В качестве меры рассогласования L в работе использовалась квадратичная ошибка:

L ( Hq ( Х ), У ) = Е( Hq ( ^" -У-)2.

Ансамблем нулевого уровня H ₀( х ) является непараметрическая оценка

H 0 ( X ) =

nm

K i=1 j=1

X j "

j c 0

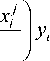
nm

ЕП K

= 1 j = 1

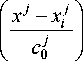
где с о - вектор параметров размытости.

Каждая последующая непараметрическая оценка дополняет текущий ансамбль H_{q -} i ( X ), минимизируя невязку между выходом объекта у и выходом текущего ансамбля H_{q -1}( Х ):

^Hq ( ^Х ) = ^Hq " 1 ( ^Х ) ^{+ <}

nm

ЕПк

= 1 j = 1

f X j

^^^^^^а

x j

^{( y}i

" ^Hq " 1 ^{( Х}- ) )

nm

ЕП к

i = 1 j = 1

xj

^^^^^^а

^xi ^j

nm

ЕП к

' x

^^^^™

Х/

c q

j cq   '                п q = 1, 2, ..., Q.

0,

= о,

В результате задача построения ансамбля непараметрических оценок сводится к следующей задаче оптимизации:

W = L (HQ (x), y )^ min, Q            C,Q где Q – количество непараметрических оценок, включенных в ансамбль; C – последовательность векторов параметров размытости:

C = { c 0 , c l , ..., c Q } .

Однако оптимизация параметров размытости при добавлении каждой модели при большом объеме обучающей выборки требует большого количества вычислительных ресурсов. Вычислительная сложность зависит от выбранного метода оптимизации и от решаемой задачи и может быть оценена как O( kñn ) на каждом шаге, где k – количество вычислений критерия, ñ – объем валидационной выборки. Значение k при этом может быть достаточно большим (особенно в случае высокой размерности пространства входных переменных). Для того чтобы избежать данной проблемы, в данной работе предлагается алгоритм последовательного пересчета параметров размытости, гарантирующий вычислительную сложность O( mñn ) на каждом шаге, где m – размерность пространства входных переменных. Параметры размытости пересчитываются по следующим формулам:

12    m

Jr¹ r² r ™ = J haq r¹ . hq^qc¹ ,      haq m I

• | cq , ^cq , ..., ^c q ( । ^cq —1,^ ^cq —1 , ^..., ^cq —1 | ,

m aq е{0,1}, E aq = 1, j=1

где значения вектора ͞ a q указывают на то, какой именно параметр размытости должен быть уменьшен на шаге q . Для того чтобы определить значения ͞ a q , последовательно уменьшаем по одному из параметров размытости, строим оценку невязки текущего ансамбля, добавляем эту оценку к текущему ансамблю и вычисляем значение критерия качества. На основании значений критериев качества присваиваем следующие значения компонентам вектора ͞ a q : a^j q = 1, если уменьшение j -го параметра размытости привело к наибольшему увеличению точности ансамбля, иначе a^j q = 0. В случае получения одинаковых значений критерия качества при уменьшении нескольких параметров, произвольным образом выбирается один из этих параметров размытости, соответствующая ему компонента вектора ͞ a q равна 1, остальные компоненты равны 0.

Вектор начальных параметров размытости ͞с0 должен быть таким, чтобы оценка (1) существовала для любого вектора входных переменных x͞, каждая компонента которого лежит в интервале от минимального до максимального значений соответствующей компоненты, определенных по имеющейся обучающей выборке. Для того чтобы избежать дополнительных рас- четов оценки (1) вектор начальных параметров размытости ͞с0 может быть выбран следующим образом:

c^J o = max ( x{ ) — min ( x^j ) , j = 1, 2, ..., m.

Параметр b непосредственно влияет на количество непараметрических оценок, которые будут включены в ансамбль: чем меньше b , тем быстрее ширина ядер в оценке (1) уменьшится до таких значений, что ядра перестанут захватывать наблюдения и процесс построения ансамбля прекратится. Выбор наилучшего параметра b можно сравнить с попыткой предсказать параметры размытости последней модели в ансамбле, а затем подобрать b , исходя из требований к количеству моделей в ансамбле. Параметры размытости последней модели связаны с особенностями решаемой задачи: распределения входных переменных, наличие сгустков наблюдений в обучающей выборке, плотность этих сгустков и т. д. Причем эта оценка всегда будет оценкой снизу, так как выполняется до построения ансамбля. Если b будет вычислен исходя из требования к количеству моделей в ансамбле, значение b может оказаться завышенным. Завышенное значение b приведет к остановке роста ансамбля при меньшем количестве моделей. Так как b непосредственно характеризует скорость изменения параметров, то завышенное b приводит к более быстрому уменьшению параметров размытости, что сказывается на точности. По этой причине построение нескольких ансамблей с различными значениями b и последующим выбором наилучшего представляется более выигрышной стратегией. Параметр b должен выбираться из диапазона от 0,5 до 1. На основании множества разнообразных численных экспериментов и решения прикладных задач идентификации рекомендуемое значение параметра b = 0,8. Данное значение параметра в большинстве задач позволяет получать достаточно высокую точность при небольшом количестве моделей в ансамбле.

Оценка в разреженных областях пространства входных переменных. Покажем работоспособность данного подхода в условиях наличия разреженных областей в пространствах входных переменных.

Рассмотрим следующий численный эксперимент. Пусть имеется единственная входная переменная x , принимающая значения от 0 до 3, структуру объекта зададим уравнением y = x ² + 10. После формирования обучающей выборки извлечем из нее все наблюдения со значением входной переменной от 1 до 2. К получившемуся набору данных применим предлагаемый подход к построению ансамблей непараметрических оценок регрессии. На рис. 3 показаны ансамбли, состоящие из одной, двух и пяти моделей.

Сравнение единственной непараметрической оценки регрессии и предложенного в работе ансамбля приведено на рис. 4.

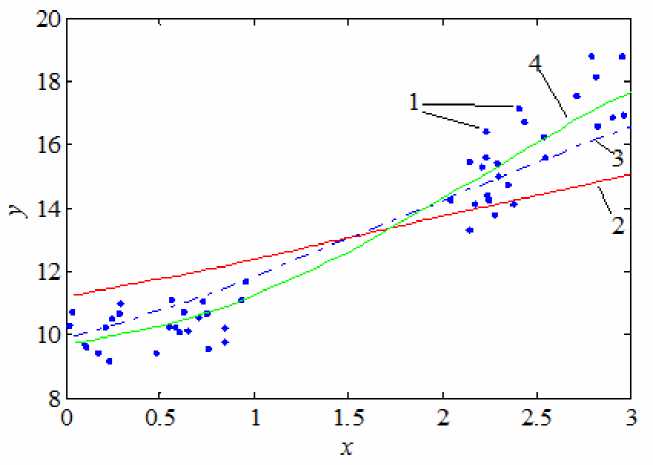
Рис. 3. Построение ансамбля непараметрических оценок (1) для разряженных областей:

1 – обучающая выборка; 2 – базовая оценка; 3 – ансамбль, состоящий из суммы двух непараметрических оценок; 4 – ансамбль, состоящий из суммы пяти непараметрических оценок

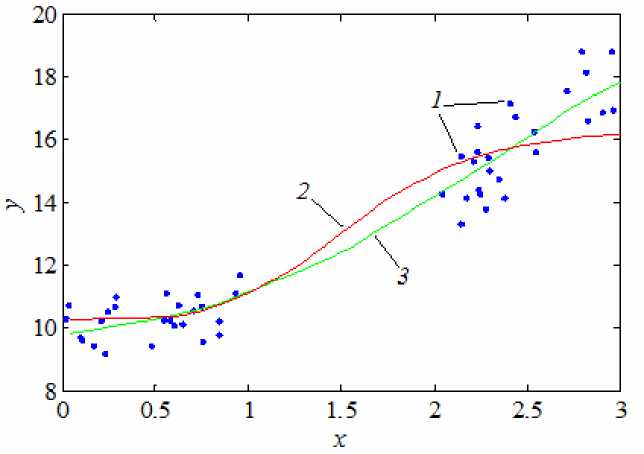
Рис. 4. Сравнение единственной непараметрической оценки регрессии и ансамбля для разряженных областей:

1 – обучающая выборка; 2 – непараметрическая оценка регрессии с настроенным параметром размытости; 3 – ансамбль, состоящий из суммы пяти непараметрических оценок

В ходе численных исследований было показано, что точность ансамбля непараметрических оценок Надарая–Ватсона превосходит единственную оценку как в разреженных областях пространства входных переменных, так и в областях с большим количеством наблюдений. Следует также отметить, что для многомерных задач разница в точности между ансамблем и единственной оценкой становится более значительной.

Оценка на границах пространства входных переменных и экстраполяция. Добавление каждой последующей непараметрической оценки в ансамбль направлено на то, чтобы уменьшить ошибку текущего ансамбля. Поэтому большое влияние на итоговую оценку оказывают наблюдения, близкие к границе области входных переменных, так как в силу особенности своего построения точность непараметрической оценки у границы меньше [14], а следовательно, больше значения невязок между выходом объекта и выходом текущего ансамбля и больше вклад в итоговую оценку.

Рассмотрим следующий численный эксперимент. Пусть имеется единственная входная переменная x, принимающая значения от 0 до 3, структуру объекта зададим уравнением y = x2 + 10. Оценку будем строить на интервале от 0 до 4. К получившемуся набору данных применим предлагаемый подход к построению ансамблей непараметрических оценок регрессии. Последовательность ансамблей H0(x), H1(x), …, H4(x) показана на рис. 5. Нетрудно видеть, что вблизи гра- ничных значений (0 и 3) различия между этими ансамблями больше.

Сравнение единственной непараметрической оценки регрессии и предложенного в работе ансамбля приведено на рис. 6. Следует отметить, что ансамбль непараметрических оценок может быть использован и для экстраполяции.

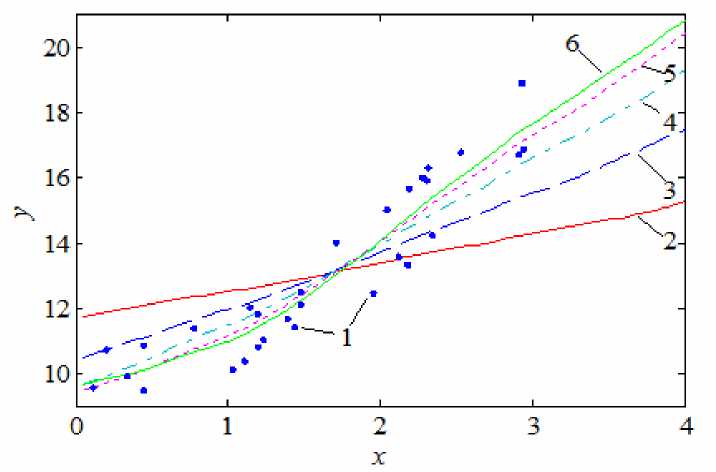
Рис. 5. Построение ансамбля непараметрических оценок (1) для границы области входных переменных:

1 – обучающая выборка; 2 – базовая оценка; 3 – ансамбль, состоящий из суммы двух непараметрических оценок; 4 – ансамбль, состоящий из суммы трех непараметрических оценок; 5 – ансамбль, состоящий из суммы четырех непараметрических оценок; 6 – ансамбль, состоящий из суммы пяти непараметрических оценок

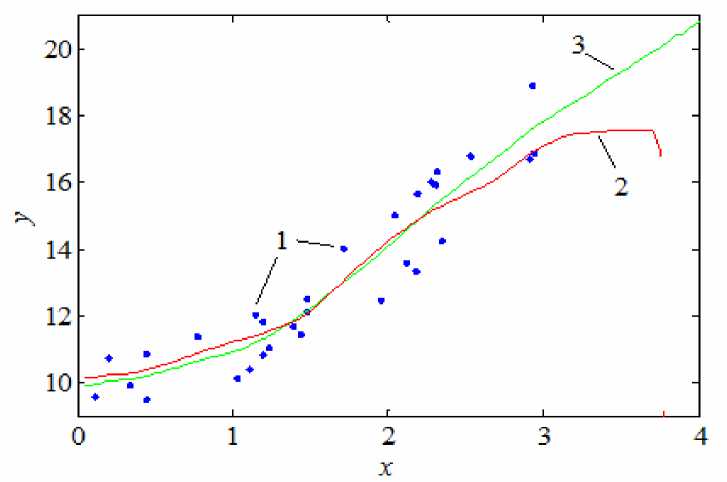
Рис. 6. Сравнение единственной непараметрической оценки регрессии и ансамбля для границы области входных переменных:

1 – обучающая выборка; 2 – непараметрическая оценка регрессии с настроенным параметром размытости; 3 – ансамбль, состоящий из суммы пяти непараметрических оценок

В ходе численных исследований была показана высокая эффективность предложенного ансамбля при оценке вблизи границ области входных переменных, а также за ними. Для многомерных задач разница в точности между ансамблем и единственной оценкой становится более значительной.

Заключение. Предложен подход к обучению ансамбля непараметрических оценок Надарая–Ватсона, позволяющий повысить точность восстановления зависимости между входными переменными и выходной переменной по наблюдениям. Разнообразные численные эксперименты свидетельствуют о высокой эффективности предложенного подхода к формированию ансамблей непараметрических оценок при наличии разреженных областей в пространстве входных переменных, а также на границах этого пространства.