О построении эволюционных определяющих уравнений
Автор: Новокшанов Р.С., Роговой А.А.
Статья в выпуске: 9, 2001 года.
Бесплатный доступ
Подход к построению конститутивных уравнений релаксационного типа с необходимостью, ротационные производные был сформулирован на основе связей между различными: формами тензора напряжений и объективными производными.
Короткий адрес: https://sciup.org/146211809
IDR: 146211809 | УДК: 539.3
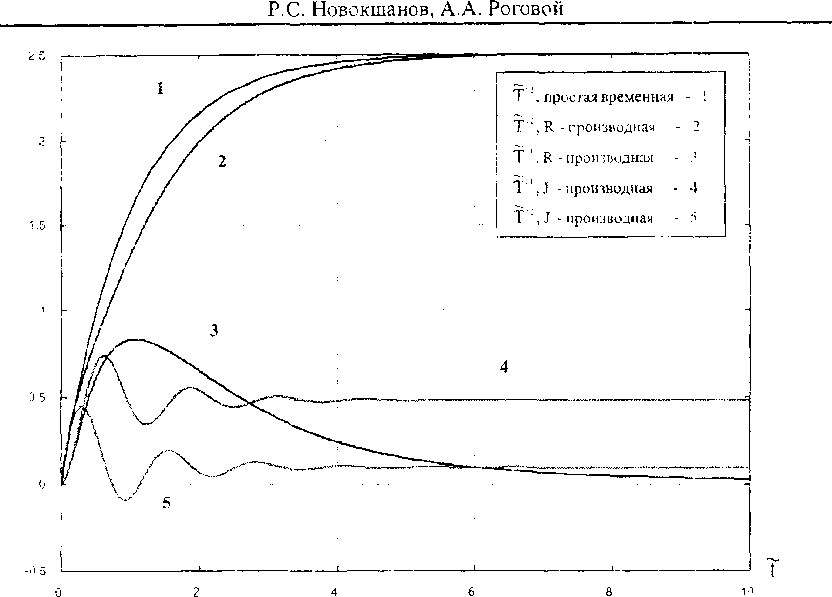
Текст научной статьи О построении эволюционных определяющих уравнений
Здесь J -третий главный инвариант градиента места F,
Т, =Rr-T-R=7”7r/ry = T:jffJ = Tijt,rj = 7Vfzr,.
-
- вращательная форма тензора напряжений (повернутый тензор) [3].
Т2 =F-'.T-F"r = Tiji1rj
-
- верхняя конвективная форма тензора напряжений (энергетический тензор) [3],
Т3 = F7-Т-F = 7); г! г7
-
- нижняя конвективная форма,
T4 = F ! T F =7(r,r#
-
- правая и
- Т5 =Fr Т F"r = 7 г г,
-
- левая конвективные формы тензора напряжений [5],
Т6 = J F"1 Т •F~r = J Г’ г, r; = JT2
-
- второй (симметричный) тензор Пиола - Кирхгоффа и
- Т7 = J F T = J T^W,
-
- первый (антисимметричный) тензор Пиола - Кирхгоффа. Конечно, каждый из этих тензоров, например Т2, может быть записан во взаимном и смешанном базисах, но
ковариантные и сметанные составляющие тензора Т, при этом, естественно, не будут совпадать с ковариантными и смешанными составляющими тензора Т .
Выписанные выше тензоры примечательны тем, что с их помощью легко строятся коротационные производные, необходимые для объективности (материальной независимости от системы отсчета) эволюционных определяющих уравнений. Так R- производная (известная еще как производная Зарембы, Грина - Нагди, Грина -
МакИнниса, Диенеса)
TR =t-®T + Tty = R-T1Rr, производная Олдройда
Т0'= t-1 Т-Т I5 =F t2 Fr =Г^ ^ Т2 = Г'; г; г;.
производная Коттер-Ривлина
TfM+l7l + TJ =F■ЦT'1=7;VR'R,■, Т3 = Т:уг!г;. (ID) левая конвективная производная
Т7 =Т-1Т+Т ! = F t4 F 1 =^R.R\ Т^г-гд правая конвективная производная т^'= t+it-t-tj7 = f-7'45-f'1 =77R\^^^ 'Г^г/Гг,,с:?
производная Яуманна
Т^1(То' +тСА) = 1(т^ дТ ^^Т-зу Т + Т w = R trR7
производная Трусделла
Т7> =t-LT-T.|r +Т tr^J-'F-T^F7 = tu R.R + Г tri.(14)
производная Хилла
Тя =Т 1 Т + Т tri FT,.
Здесь
(9=R-Rr, 1-F F 1 =(VR)r -(Vx)7 = W = ~(1 - Г) = Известны и другие коротационные производные [2, 6], а их общая форма имеет вид [6] Т* = Г" + OjD Т + ^T DtщТ tri, где D = (l + ly)/2-тензор деформации скорости. Придавая коэффициентам я л, и а; определенные числовые значения, получаем все, выписанные выше, корогашишные производные (за исключением ^-производной) и множество других. Легко определяются также производные Д-ro порядка: rj-’7? . /? __ J^ iqp -J^ Г Т^^^* ТСЙ ■ -R г / ! ! Т7'"7=F-T4-F*1, т^г.д,=F-7/rr.F7! .хт,^.тг j-lF у ,р/ Тя-я = J-'F-Tt. Здесь Т,- - .V -ая производная по времени тензора Т. Определяющее уравнение релаксационного типа Общую форму определяющего соотношения релаксационного типа N -го порядка можно представить в виде [5] Ф](F, F,..F, Т, Т,.Т) = О, (17) где Ф, - скалярная, векторная или тензорная функция. Исходя из принципа объективности (материальной независимости от системы отсчета), формализацией которого в данном случае будет соотношение (полагая Ф| тензорной функцией) Ф^Г, Г,...,Р',Г,Т,...,Г) = Ф,*(Р,Р,...,Р,Т, Т,...,Т) = 0. где F-O F, Т=ОТОГ, Ф)'=О Ф1О1и О - любой ортогональный тензор, получаем, положив О = R7 , используя полярное разложение градиента места Г = R I и учитывая соотношение (7), ( МN ) Ф, U,U,...,U,T],T1,...,T1 =0.(18) Таким образом, для выполнения принципа объективности аргументами в определяющем уравнении (17) могут быть только чистая деформация U и повернутый тензор напряжений Tt. Из соотношений (6) вытекает связь между Г и Т, z = 2*6: Т] ^^-U^-^-U'^U-T^U-^U-'-TvU^^U-VU, и тогда определяющее уравнение (18) может быть представлено в эквивалентных формах Ф,.((и},{Т,}) = 0, z = i + 6,(20) где {U) = U. U,...,U; {Г,} = Д, Т„..Т,. Рассмотрим некоторые частные случаи использования выражения (20) для построения определяющих уравнений. Конкретизируя тензорные функции Ф, в соотношении (20) для материала дифференциального тапа зависимостью Ф,({и}, {Т,}) = g;({U})-Т, = 0, где g)({U})- отклик материала на чистую деформацию, приходим к следующим определяющим соотношениям: T^g/JU}). Любое из этих уравнений удовлетворяет аксиоме Нолла [7] и функции g,({U}) связаны между собой соотношением типа (19) g, = 1^2л! = и~Ч3/и~! =u-g4.u-’ = и"^5^ Заметим, что простой физический смысл имеют функции g, и g6. Первая определяет истинные (усилие, отнесенное к текущей площади), а вторая условные (усилие. отнесенное к начальной площади) напряжения при отсутствии вращения. Поэтому экспериментально легче определять их. Конкретизируя тензорные функции Ф, в соотношении (20) зависимостью Ф,({и}, {Т;}) = G,(U, L) - Т, -zt, = 0, приходим к следующим соотношениям: I, 4-ЛТ, = С,(и, L). 122) Переходя с помощью зависимостей (6) и (8) - (14) к истинным напряжениям, получаем уравнения состояния с согласованными объективными производными (здесь термин “объективные” преобретает второй смысл: коротационная производная не назначается, что делается во многих случаях, а получается естественным образом): Т + ЛТ* = RG R'. Т + ЛТо; =FG2Fr, T + tTcs = F G F т + лтЛ = fgf, т+лт*' = f gf т+лт7" =r1FG„F;. Как уже отмечалось выше, Т) - это истинные напряжения при отсутствии вращения. Полагая в соотношении (22) G, ^//((MJ-' + U^U), что соответствует тензору деформации скорости D при R, тождественно равном единичному тензору (см. (15)), приходим в терминах истинных напряжений к определяющему соотношению Т + дТя=дО, (23) где и - коэффициент вязкости. Это хорошо известное уравнение для среды Максвелла, обобщенное на конечные деформации [8]. Необходимый тип коротационной производной здесь, что до сих пор является предметом обсуждения многих работ, выявился автоматически. На рисунке приведены результаты решения уравнения Максвелла для задачи простого сдвига. Уравнение (23) обезразмеривалось: ItID Здесь D=AD - безразмерный тензор деформации скорости, Т-лТ/^ - безразмерный тензор истинных напряжений, Тй - X" Тя 1 р и введено безразмерное время (в единицах времени релаксации) 7 = /77. Для сравнения на этом же рисунке покатаны кривые напряжений, полученные при использовании в соотношении (23) обыкноьсшюй временной и яуманновской производных. Рис. Обезразмсренное уравнение Максвелла с простой производной.. R- и J -объективными производными в задаче простого сдвига (приведены ненулевые компоненты тензора напряжений) Компонента Г12 при использовании R-производной практически совпадает' с решением классического уравнения Максвелла. Но при этом, в отличие от обычной производной, возникают нормальные напряжения, отвечающие экспериментальным данным [9], известным в литературе как эффект Вейссенберга. Осцилляции, характерные для яуманновской производной, описаны, например, в [10, II]. Использование производных Олдройда и Коттер - Ривлина приводит к симметричной относительно нуля линейной зависимости компонент Т'-, что противоречит смыслу вязкоупругого материала (нет релаксации напряжений). Компоненты же Т'" в этих случаях совпадают с решением уравнения Максвелла для простой производной. Модифицированное уравнение Максвелла [5] также вытекает из (20), полагая Ф,({U}, {Т,}) = G,(U, U)- т, - Y4 т = о и представляя G; в виде G^Go+^A.Go, где Gi^yA^-U-'+U-'-U), а Т] и Go - к-ые производные по времени от соответствующих тензоров. В терминах истинных напряжений, учитывая выражения (16), получаем Т + ^ Л = // (D + X A D1 ). к=\ и Таким образом, для определяющего уравнения релаксационного типа использование тензоров напряжений 1) + Т6 (6) автоматически приводит к согласованным коротационным производным (8) - (14) в эволюционных уравнениях состояния. Работа выполнена при поддержке гранта РФФИ-ГФЕН № 01-01-96494.