О построении линий разрыва напряжений для двумерной пластической области

Линия разрыва напряжений – это некоторая линия (поверхность) в теле, на которой напряжения терпят разрыв. Причина появления разрывов при плоской деформации – переопределён-ность граничной задачи в окрестности особой точки с какой-либо одной стороны от контактной границы. Как правило, линии разрыва расположены в более прочной части соединения [1 – 2]. При исследовании критического состояния и прочности конструкций необходимо учитывать это явление. То же относится и к стержневым конструкциям [1 – 5], и тонкостенным цилиндрическим оболочкам, где также имеет место переопределенность граничной задачи. Задача осложняется, если материал полосы неоднороден в менее прочной или (и) в более прочной части соединения [6].

Для построения линий разрыва напряжений, в случае плоской деформации, необходимо учитывать, что они находятся в точке пересечения линий характеристик одного семейства и направлены по биссектрисе угла образованными этими характеристиками. Поэтому для нахождения этих линий необходимо построить характеристики. Проше всего это сделать для задачи кручения, поскольку в этом случае характеристика направлена по нормали к внешнему контуру и найти линии скольжения и их точки пересечения достаточно просто. Этому посвящено достаточное количество работ о пластическом кручении изотропных цилиндрических и призматических стержней в случае, когда боковая поверхность стержней свободна от касательных нагрузок, а также в случае, когда боковая поверхность стержня находится под действием внешнего переменного давления [7; 8]. Кручение анизотропных цилиндрических и призматических стержней исследовано в [9 – 11]. В [12] определено предельное состояние сектора анизотропного кругового кольца при кручении. В [13] показано построение полей характеристик для цилиндрического стержня по произвольной поверхности текучести. В [14 – 17] рассматривались поверхности разрывов деформаций в упругопластических средах.

Для задач плоской деформации пластичного материала разрывные решения построить не просто. Это объясняется необходимостью рассматривать два семейства характеристик и сложностью построения этих линий скольжения. Для решения этой задачи построим непрерывную деформацию двух точных решений: гомотопию решений Прандтля и Надаи. Найдем точки пересечения линий скольжения одного семейства и построим линии разрыва.

Гомотопия решений Прандтля и Надаи

Рассмотрим систему плоской идеальной пластичности Треска – Сен-Венана – Мизеса, состоящую из двух уравнений равновесия и условия пластичности:

-' = о,      +^ = o.

d x    d y         d x d y

( ° x -° y ) 2 ⁺ 4 ^T 2 y = ⁴ k 2 ,

где σ x , σ y , τ xy – компоненты тензора напряжений; k – предел текучести при чистом сдвиге. Заменой, продолженной М. Леви,

° _x = °- k sin2 0 ,

° y = ° + k sin 20, т xy = k cos 20,

система (1) сводится к квазилинейной системе:

d°d

2 k —cos20+sm20l = 0, dx    (5x        dy d°  ^A^''

2 k —sin20+cos20l = 0, dy     (dx        dy

в которой о - гидростатическое давление; 0---угол между первым главным направлением

тензора напряжений и осью OX .

Решение Прандтля часто используется для описания сжатия жесткопластического материала шероховатыми плитами. Предполагается, что слой имеет значительно большую длину по сравнению с его толщиной. Это решение приближено описывает реальную ситуацию в некотором отдалении от центра слоя, если начало координат расположено в центре слоя.

В терминах переменных σ, θ для системы (2) это решение имеет вид

° = - p 1 - k

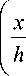
1 -

y ²

h ²

y = h cos2 0 ,

где h = const; y = ±h – границы плит; p 1 = const.

Граничные решения примут вид

0| _y = _h = n n , n eZ ,

°| y = h =^- p l ^- k y. h

Характеристики решения имеют следующий вид:

x = h (2 0- sin 2 0 ) - h

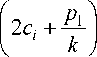
y = ± h cos 2 0 , i = 1,2,

где c_i – const.

Решение Надаи описывает пластическое положение вокруг круглого отверстия радиуса R , нагруженного равномерно распределённым нормальным давлением p₁ = const и нулевым касательным напряжением на контуре отверстия. Данное решение можно записать в виде

n ⁰=ф₊ 4,

22        2

x ⁺ y ^Г ° = - p ₇ + k + k In---- — = - p ₇ + k + k ln—-, 2 R 2 2 R 2

где r ; φ – полярные координаты.

Граничные условия принимают вид

°| r = R = Ф+ 4, °| r = R = P 2 + k .

Получившиеся линии скольжения имеют следующей вид:

n _ ( „ P o - k ф = 0 , r = R exp ±0 + —-- + c,

4              (        2 k      '

где c i – const; i = 3,4.

Выразим решение Надаи и Прандтля как решение линеаризованной системы:

/      \ P 2 — k ° x = cos 0-— Re 2k e2k,

V 4 )

/      \ P 2 - k ° y = sin 0-— Re 2k e2k,

V    4 )

h ° pxh x =----1--h sin 20, kk y = h cos 20 .

Выполняем гомотопическую линейную комбинацию решений Прандтля и Надаи:

К К           A             ( A   P 2 - k ° x = a

— - p ¹— h sin2 0 + ( 1 - a ) sin 0-— Re ^{2 k} e ^{2 k} , k k ) ^V V 4 J

/ X     p 2 - k °

П y = h cos 20- (1 - a )cos l0- —I Re 2 k e2 k ,

где a – групповой параметр.

Получаем граничную кривую для решения (10):

n

° = - p ₁ + k ; 0 = ф + .

Подставляя σ = 2 k ( a + θ) в систему (3), получаем параметрические уравнения семейства линий скольжения:

p,          A             p-r-k    ( nA x = ah 2 (c +0) + — + sin20 +(1 - a) Re 2 k cos 0- e + ,

V ^{v 1 !} k )                        V 4 )

p 2 - k    _{( A}                                   (12)

y = ah cos2 0 + (1 - a )Re ^{2 k} sin [0-- 4- 1 e a ⁺⁰ .

При этом мы можем наблюдать эволюцию характеристик, которые зависят от группового параметра a , при a = 1 получаются характеристики решения Прандтля (рис. 1).

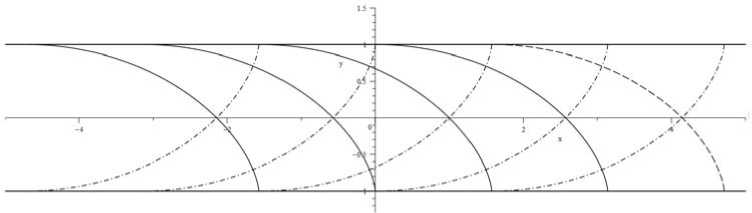
Рис. 1. Преобразованные линии скольжения: h = 1; p 1 = p 2; a = 1

Fig. 1. Transformed sliding lines: h = 1; p 1 = p 2; a = 1

При a = 0 характеристики решения Надаи представлены на рис. 2.

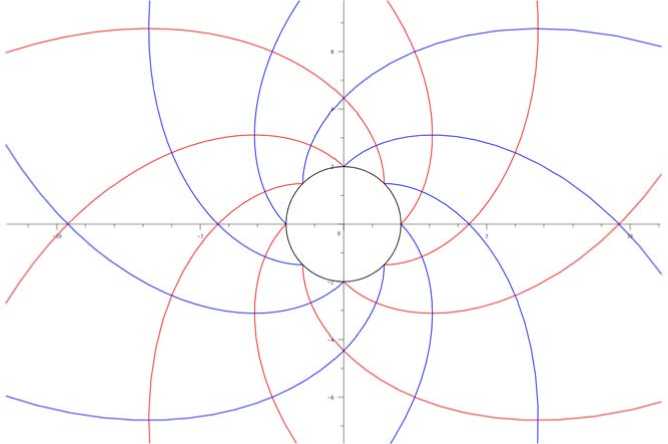
Рис. 2. Преобразованные линии скольжения: a = 0

Fig. 2. Transformed sliding lines: a = 0

При a = 0,5 характеристики одного семейства начинают пересекаться и возникают линии разрыва напряжений, как на рис. 3.

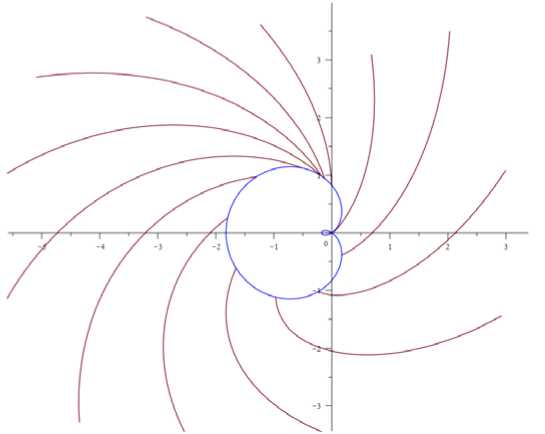
Рис. 3. Пересечение линий скольжения для отверстия в виде улитки Паскаля a = 0,5

• Fig. 3.    The intersection of the sliding lines for the hole in the form of a Pascal snail a = 0,5

Так как характеристики одного семейства пересекаются, то значения вдоль них различны, и решение задачи Коши после точки пересечения не может быть продолжено непрерывно, возникает линия разрыва напряжений. Эта линия разрыва проходит по биссектрисе угла, образованного пересекающимися характеристиками, и выходит из точки их пересечения в координатах [– 0,183;0,991] (рис. 4).

Рис. 4. Линия разрыва напряжений

• Fig. 4.    Stress discontinuity line

Заключение

В данной работе построена гомотопия двух известных точных решений: Прандтля и Надаи, т. е. непрерывная трансформация одного решения в другое. При этом можно наблюдать эволюцию характеристик, которые зависят от группового параметра a : при a =1 получаются характеристики решения Прандтля; при a =0 – характеристики решения Надаи; при a =0,5 характеристики одного семейства начинают пересекаться и возникают линии разрыва напряжений, которые проходят по биссектрисе угла пересечения характеристик и выходят из точки их пересечения. Если продолжить увеличение параметра α пересекающихся характеристик становится больше что усложняет построение линии разрыва напряжений. Решение этой проблемы будет рассмотрено в дальнейших работах.