О построении модели бесплатформенной инерциальной навигационной системы авиабомбы с неинвариантными алгоритмами обработки информации

Анализ существующих тенденций развития авиационного вооружения убедительно показывает, что в настоящее время и в ближайшем будущем основное внимание специалистов должно уделяться созданию и совершенствованию высокоточного «интеллектуального» оружия, обеспечивающего эффективное «точечное» поражение целей в любых условиях, независимо от противодействия противника, в том числе с помощью активных или пассивных помех [1].

Таким образом, весь арсенал последних достижений в области решения навигационных задач, таких как GPS/ГЛОНАСС технологии, бесплат-форменные инерциальные системы, микромеханика и другие могут и должны быть использованы для создания управляемых и корректируемых авиационных бомб.

В работах [1,2] приводятся различные схемы комплексирования БИНС со спутниковыми навигационными системами (СНС): раздельная, слабосвязанная, жестко связанная, глубоко интегрированная схемы. Все они имеют свои преимущества и недостатки, но потенциальная точность выходной навигационной информации в них повышается за счет применения специальных схем комплексирования и алгоритмического обеспечения.

В данной работе ставится задача на исследование метода повышения точности выходных навигационных параметров БИНС за счет использования информации о динамических свойствах объекта.

Идея оптимизации алгоритмов ИНС на основе учета динамических свойств объекта не нова. В работах [3,4] затронуты вопросы повышения эффективности навигационных алгоритмов для объектов с известной динамикой.

В настоящей работе предлагается методика построения алгоритмов для БИНС с учетом линеаризованных уравнений движения У АБ на основе расширенного фильтра Калмана. Предлагается непосредственное включение оцениваемых навигационных параметров в вектор состояния.

1.    Постановка задачи неинвариантной обработки информации в БИНС

В настоящей работе используются следующие правые прямоугольные системы координат (СК) [5]:

• •    инерциальная О_оХ_И¥_И7_И с началом в центре Земли, оси Х_И и Z_H которой направлены в точку весеннего равноденствия и по оси мира

(вращения Земли) соответственно, ось Уи образует правую ортогональную тройку (рис. 1);

• •    гринвичская О_ИХ¥Х, связанная с Землей, ось X которой проходит через пересечение гринвичского меридиана с экватором, ось Z совпадает с Z_H, а ось К также образует правую ортогональную тройку;

• •    сопровождающий навигационный трехгранник OENU с началом в центре масс обьекта-УАБ, оси Е, N и U которого направлены по географической параллели на восток, по меридиану на север и по местной вертикали вверх соответственно;

• •    связанная с объектом Oxyz, оси х, у и z которой совпадают с главными осями инерции УАБ и направлены (относительно конструкции) вперед, вверх, и вправо соответственно.

2.    Модель движения У АБ

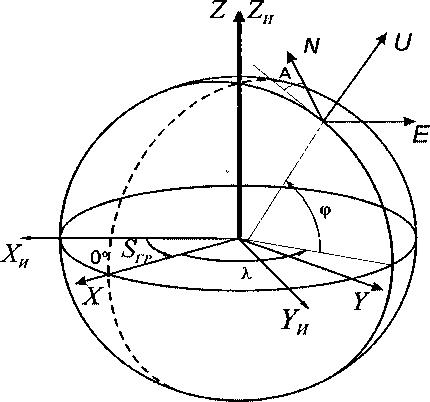
Рис. 1. Системы координат, используемые в БИНС

Задачу неинвариантной обработки информации в БИНС сформулируем следующим образом.

Будем считать, что гироскопы и акселерометры измеряют составляющие абсолютной угловой скорости УАБ и ее кажущиеся ускорения по связанным осям. Датчики положения аэродинамических рулей позволяют измерять управляющее воздействие на бомбу: отклонение руля высоты 8В, элеронов 8Э и руля направления 8Н. Стохастическая модель движения УАБ известна.

На основе измеряемых сигналов первичной инерциальной информации, а также сигналов управляющего воздействия на объект, используе- мых совместно с известной стохастической моделью его движения, требуется оценить параметры движения объекта.

Кинематические уравнения для поступательного и вращательного движения имеют вид [3, 5]:

Х = ^/((Д-ь/Осозф);

4> = W_N/(R + hy,                         (1)

h = Wu;

С = С^ х]-[щ™и х] С.       (2)

Здесь X, ф и h - географические координаты У АБ (долгота, широта и высота соответственно); WE,WN,WV - проекции на оси навигационного трехгранника ViENU - вектора скорости движения У АБ относительно Земли, которую в целях упрощения принимаем шаром радиуса R; ^ENU _р. QCOSф. ОзШф] _ угловая скорость вращения Земли в проекциях на оси навигационного трехгранника, ю™и =[-ф; Хсозф; Хзшф] - угловая скорость навигационного трехгранника относительно гринвичской системы координат; ®дм/и2и £1enu + ®™и - угловая скорость нави гационного трехгранника относительно инерциальной СК, определяемая вращением Земли и движением центра масс У АБ.

Поскольку из девяти элементов матрицы ориентации С независимыми являются только три, то при ее нахождении применяются различные варианты параметризации, например с помощью эйлеровых углов рыскания ф, тангажа и и крена у.

Матрица С с элементами су, i, j = 1,2,3 имеет сле дующий вид:

cn = -зшфсози;

С12 = 8Шф8ШиСО8у + СО8ф8Шу;

с13 = - sin ф sin и sin у + cos ф cos у;

^3x3 -

с21 = cos ф cos и;

с22 =-cos ф sin и cosy + sin ф sin у;

с23 = cos ф sin и sin у + sin ф cos у;

с31 =sinu;

с32 = cos и cos у;

с33 =-cos и sin у.

С учетом (3) уравнение (2) может быть записано в виде:

Ф = l/cosu^ cosy-o>z sin у);

■ и = ю^ siny+

у = <вх -tgu(

Вектор относительной угловой скорости вычисляется по измерениям гироскопических датчи ков с учетом известной скорости вращения навигационного репера:

^ = й™ -С5™и = [о,; о,;

х[8Шф8ши; - cos ф sin и; cosv] +

+(cos ф sin у + sin ф cos у) [cos ф; зтф; 0]] .      (5)

Поступательное движение УАБ в инерциальной системе координат подчиняется основному закону динамики, который в проекциях векторов на оси навигационного трехгранника имеет вид:

V^NU = 1/М ■ CF^ + g^ENU -

-(гСй^х]^®^])^,     (6)

где М - масса объекта, F^ - аэродинамическая сила, действующая на объект, в проекциях на оси связанной СК.

Вращательное движение УАБ также описывается дифференциальным уравнением, вытекающим из основного закона динамики вращательного движения. Для УАБ, главные оси инерции которой совпадают с осями связанной СК, наиболее простой вид это уравнение имеет в проекциях на эти оси [3]: ^Tnu = (J^)"¹(m^-[^x] J*^),  (7)

где

J^=diag3x3(j„^,J:)              (8)

матрица моментов инерции, J_x,J_y,J_z - моменты инерции УАБ относительно осей связанной СК (главные моменты инерции УАБ).

Аэродинамическая сила F^2, действующая на УАБ, определяется конфигурацией бомбы и характером обтекания ее воздушным потоком. В проекциях на оси связанной СК она может быть представлена в виде [3]:

^ =qSVc_x; с_у, c^_f.           (9)

Здесь ^ = рК_Во_ЗД/2 - скоростной напор; р -плотность воздуха, зависящая от высоты полета; К_возд ~ величина воздушной скорости; S - характерная площадь УАБ; c_x,c_y,c_z - безразмерные аэродинамические коэффициенты, получаемые в результате испытаний изделия в аэродинамической трубе и аппроксимируемые в соответствии с моделью:

Сл=^(а) + с5в(а)8в;

- 5 =су(а) + с®в (а)5в;                (10)

с, = с? (а) р + с?^н (а)8_н.

где аир- углы атаки и скольжения УАБ, 8В,8Н — величины, характеризующие управляющее воздействие отклонения руля высоты и руля направления соответственно, wу - трехмерный вектор взаимно некоррелированных белых шумов, интенсивность которых определяется степенью неточности модели (10).

Таким образом,

Е£№/=СГПрЛ03д,а,Р,8в,8н^^^^

Аэродинамический момент сил, определяющий вращательное движение У АБ, в проекциях на оси связанной СК имеет представление, аналогичное (9):

m™ = <7S/diag(l, 1,1)[т_х; т_у; m,] + w_m, (12) где / - длина корпуса УАБ; т_х, т_у, m_z - безразмерные коэффициенты аэродинамических моментов, аппроксимируемые в соответствии с моделью:

т_х=т_х^а.,^*т^ (a)o_x + +^ (a)^ + ™? (а)б_э + m®^H т_у = т_у^а,^ + т_у^х (а)а)_х +

CO

(а)5н;

+т^ (а)р + т_у^э (а)8_э + т®^н (а)8_н;

a =

P =

где

^mz ^{= m}z (^a) ^{+ m<}z‘ +m^ (a)5_B.

a +

где 8Э - управляющее воздействие в виде отклонения элеронов; wm - трехмерный вектор взаимно некоррелированных белых шумов, интенсивность которых определяется степенью неточности (13); чертой обозначены безразмерные угловые скорости:

co

о,,, ®z

='

= /о^/(2ЕВ0ЗД);

= /гаг/(2КВ03Д);

“ = /а/ЕВ03Д;

.^ = ФКзд.

Таким образом, m^ =m^'z(a,P,d,p,(ox,to^,a)z,83,8B,

^^Wm_xlW_my,W_m2y                  (15)

Параметры движения УАБ относительно воздушных масс - воздушная скорость Ивозд, а также углы атаки и скольжения аир- могут определяться по проекциям вектора воздушной скорости на оси связанной СК:

V^ =c(w£OT/-U£W/);

у²+ у² + У² •

В03Дх г ВОЗД,, * В03Дг ’

a

л2 + К2

ВОЗДХ Г ВОЗДу

Скорость нарастания аэродинамических углов может быть определена дифференцированием выражений (16):

_у у ₊у у ' возд_х' ВОЗДу ' ' возд, ' возд_х

К² + К² ’ ^Т В03Д_х’ ВОЗДу

-V V V ^г возд_х^г возд_х^г возд_г (у²  ₊у²  ₊у² ) 1у²

I^г возд_х^{1 г} возд^, ^{1 г} ВОЗД_Х]М^Г ВОЗД;

У У У ^г ВОЗДу ’ ВОЗДу ’ возд_г

+и2

' ' возд.

возд_х⁺ ^возд, ⁺^возд₂ )^^возд_х⁺ ^возд,

У (у2  +у2  )

^г ВОЗД., I ВОЗД_Х¹ ' ВОЗДу I

'2  + у2 +у2  ) 1у2  + у2

воздх 1 ' возд, 1 ' воздх 1 Ц ' воздх 1 ' возд.

у ^г возд_х

Г ^^ = ^гВОЗДу возд

/воздг _ х/^£№_и^

to^xjCx

j^ENU _ у ENU )

Ветровое возмущение будем описывать как марковский процесс:

5£jvy=-T-1u№y +

^аи_Е ’ ^au_N * ^аи_и ) V²/^TU^WU >

где а_и - среднеквадратическое значение составляющей скорости ветра в соответствующем направлении; Ту — период корреляции ветрового возмущения; Wy - трехмерный вектор взаимно некоррелированных белых шумов единичной интенсивности.

Считаем, что измерение гироскопов и акселерометров искажено смещением нулей, ошибками масштабных коэффициентов и ориентации изме-

ригельных осей, а также ставляюшую:

имеет белошумную co-

1 + к,

e

e

^измер

Ех

E

Здесь s и

s

1 + K

E

s+As+ws. (20)

S

1 + K

гироскопов, a^z

заменяют индексы ю^ и о для и а для акселерометров, w -

трехмерные белые шумы. При этом все составляющие инструментальных погрешностей будем считать марковскими:

X_£rr - -T_ErrX_Err + a_Err 2/x_Err w_Err.

Здесь Err заменяет необходимые индексы Аю^, Aa^, к_ю , к_а (w - трехмерные векторы взаимно некоррелированных белых шумов единичной интенсивности), Ё_т, Ё_а (w - шестимерные векторы взаимно некоррелированных белых шумов единичной интенсивности).

Особенность измерения ускорения состоит в том, что собственно ускорение в вектор состояния не входит. Однако, в соответствии с (9), (10) величина ускорения связана с параметрами движения УАБ относительно воздушных масс и с управлением. Поэтому для сигналов акселерометров в (20), с учетом (10), подставляем выражение:

a^=l/M-qS^c/, с_у; с,].            (22)

3.    Вектор состояния в задаче обработки информации

Вектор состояния в задаче синтеза неинвариантного алгоритма для БИНС современной УАБ представим в виде набора векторных компонент, в числе которых:

• •    вектор Х_ХфА = [X; ср; й], включающий географические координаты УАБ;

• •    вектор X_w = [ср; и; у] параметров угловой ориентации УАБ;

• •    вектор X^_ENU = UV_E’^WN’^Wul земной скорости УАБ;

• •    вектор Х_^_Уи2и = [ш_х ;ю_у; ®_z] скорости углового движения УАБ относительно инерциальной системы координат;

• •    вектор Xqenu = [U_E-,U_N',U_u} скорости ветра, характеризующий возмущающее воздействие на УАБ;

• •    векторы, описывающие погрешности гироскопов и акселерометров: смещение сигнала Х_№^ =[^;Л®^^] и Х^ =[Аа_х; Аа^; Aa_z], ошибки масштабных коэффициентов ^Кщ “ [^Kx ’ ^кю_у ’ К»_г J ^и ^Ka ~ ^^Ка_х ’ ^Ка_у ’ ^Ka_z ] ’ ориентации        измерительных        осей

^ ⁼ k ’^xz’^yx"’ ^yz ’ ^E“>zr ’ ^Е®^ ] ’ Xe_a ~ [^Ea_w; ^Ea_xz S ^Ea^ ’ ^Ea^ ’ ^Еа_и > ^Ea^ ] •

Таким образом, имеем 39-мерный вектор состояния:

• X = ^Х_ХфА; Х_фиу; Х1 _гои; Х^_Уи2и ; х!_ЛЖ;

).           (23)

Вектор состояния (23) определяет погрешности БИНС и не поддается непосредственному измерению. Однако имеется косвенная возможность его наблюдения при получении информации от спутникового приемника. Считая его измерения достаточно точными, предполагаем, что разница между параметрами, измеренными приемником и вычисленными БИНС определяет погрешности инерциальной системы.

Далее синтезируем оптимальный дискретный фильтр Каймана, на выходе которого получаем оценку вектора состояния X [6]. На основании оценки вектора состояния X осуществляется коррекция выходных параметров БИНС. Следует подчеркнуть, что коррекции подвергаются только выходные параметры, поступающие потребителям.

Заключение

С переносом акцентов при построении БИНС в сторону более дешевых датчиков образуется ситуация, когда погрешности инерциального измерителя становятся сопоставимыми с достижимой точностью описания динамических свойств объекта навигации. Эффективным путем оптимизации алгоритмов инерциальной системы становится учет динамики объекта [3,4].

В ходе работы на основе калмановской фильтрации необходимо разработать алгоритм обработки сигналов акселерометров и гироскопов для оценки навигационных параметров УАБ.

Для оценки возможностей по повышению точности выходных параметров БИНС необходимо провести численное исследование.

В целях сопоставительной оценки точности алгоритмов, получаемых при инвариантном и неинвариантном подходах необходимо выполнить решение соответствующих уравнений для дисперсионных матриц вектора состояния.