О построении нейронных сетей для решения задачи дезагрегации данных о потреблении электроэнергии в домохозяйствах

Одной из важных задач в рамках решения стоящей перед современной цивилизацией проблемы повышения энергоэффективности является мониторинг данных об энергопотреблении в домохозяйствах. Как правило, в таких системах применяются счетчики, передающие показания в соответствующие центры обработки информации. Эти данные в первую очередв используются для выставления счетов за потребляемые ресурсы, но, как показано в работе [1], при достаточной степени их детализации могут быть использованы для подробного анализа, поведения потребителя и формирования рекомендаций об улучшении модели потребления.

В ходе этого анализа, решается задача, формирования данных об энергопотреблении отдельных устройств на. основании данных одного счетчика, установленного в домохозяйстве, который измеряет совокупное потребления всех устройств, - задача, дезагрегации данных. В литературе данный подход называют неинвазивным мониторингом нагрузки или NILM (англ. Non-Intrusive Load Monitoring).

Одно из наиболее активно развивающихся направлений в разработке NILM-методов связано с применением методов машинного обучения и нейронных сетей. При этом для

оценки эффективности разрабатываемых методов, как правило, используются некие общепринятые и ранее опубликованные в научной печати эталонные типовые модели потребления отдельных устройств, таких, как стиральная машина, холодильник и посудомоечная машина.

Наборы данных NILM обычно включают в себя как совокупную мощность нагрузки, так и нагрузку каждого исследуемого устройства, но не состояние устройства (т. е. включено оно или выключено). Следовательно, естественным образом можно сформулировать задачу регрессии как прогнозирование потребления мощности отдельным устройством по суммарной нагрузке. А задача классификации заключается в прогнозировании состояния устройства. В работе [1], предложены две архитектуры на основе рекуррентных и сверточных сетей для предсказания потребления мощности, а также исследованы методы нахождения порогов активации устройств, то есть минимального значения мощности, при достижении которого прибор переходит из выключенного состояния во включенное. Однако рассмотренные архитектуры нельзя назвать универсальными, так как для различных устройств оптимальными оказываются разные модели, а один из способов для поиска порогов активации требует подбора наилучших временных границ, о чем было упомянуто, но не реализовано авторами.

В данной работе предлагается более универсальная архитектура нейронной сети, сочетающая в себе преимущества и рекуррентных, и сверточных моделей, а также исследована возможность оптимизации временных порогов, то есть значений промежутков времени, в течение которых устройство не переходит из одного состояния в другое.

• 2.    Постановка задачи

В задаче регрессии прогнозируемые величины Р^ представляют собой мощность нагрузки 1-го устройства в момент времени j. Входная мощность нагрузки измеряется счетчиком с постоянной скоростью т, который производит серию измерений мощности Pi на каждом временном интервале. Суммарная мощность P j в момент j представляет собой сумму

L ^p j = Е ^P + т 1=1

где L — общее количество электроприборов в доме, /'( — мощность электроприбора I в момент времени j, a e j — неопределенная остаточная нагрузка. Все эти величины выражаются в ваттах.

На вход модели поступают п последовательных измерений:

Pj = (Pjn,Pjn+i,...,Pjn+n-i), где j ~ индекс сегмента последовательности. Выходом модели являются последовательности Pj£) для каждого наблюдаемого устройства в те же моменты времени. В качестве целевой метрики используется МАЕ:

,     Mrain , Lout ,

^{1   Е   1 Е} I Р^ I

М             L ₊       \^{Pji    Pji} I ’

^train j =i ^Lout i=i '

где М_гаіп — размер обучающей выборки, L_out ^— длина выходной последовательности, а P^’P j- - истинная я предсказанное мннюнис мощности для устройства I

В задаче классификации мы предполагаем, что устройство I может находиться в одном из двух состояния в момент времени j, которые равны si = 0 (состояние ВЫКЛ) и s= = 1 (состояние ВКЛ). Таким образом, критерием, в каком состоянии находится устройство, является установление порога А(1) для каждого прибора, то есть sjl) = 7 (P^ ^ лЮ) ’ где I(ж > а) — индикаторная функция. В этой работе мы использовали набор даннных UK-DALE, который является эталоном для NILM. В обучающую выборку вошли данные только по 1, 2 и 5 дому. Исходные данные были поделены на обучающую, тестовую и валидационную выборки по времени в соотношении 80/10/10 соответственно.

• 3.    Выбор порога активации

• 3.1.    Middle-Point Thresholding

• 3.2.    Variance-Sensitive Thresholding

Для выбора порогового значения мощности активации с целью определения состояния устройства наиболее часто применяются три различных способа: Middle-Point Thresholding (MP), Variance-Sensitive Thresholding (VS), Activation-Time Thresholding (AT).

В этом методе учитывается набор всех значений мощности каждого устройства, затем применяется алгоритм кластеризации k-means, чтобы разделить этот набор значений на два кластера, центроиды которых обозначаются через т^ и т^) для выключенного и включенного состояния каждого устройства соответственно. Затем находится центр тяжести каждого кластера. После чего значение порога активации А¹ каждого устройства рассчитывается как среднее значение между центроидами данных кластеров

(I) ,       (I)

_{а (/)} = ^m,,  + ш,

.

В методе VS также используется алгоритм кластеризации k-means с целью нахождения центроидов для каждого класса, но в определении порога активации А1 учитывается не только среднее, но и стандартное отклонение т/ для точек в каждом кластере по следующей формуле:

<7 (¹)

"      + 7? ’

А(1) = (1 — d)™^1) + dm^1), где ст/ — стандартное отклонение. поеннташюе для 'значений мощности 1-го устройства, отнесенного к кластеру к.

• 3.3.    Activation-Time Thresholding

• 3.4.    Нахождение порога времени

  В работе [1] порог времени

  
  

В описанных выше методах для определения пороговых значений активации устройств используются только данные распределения мощности, но часто бывает так, что из-за зашумления некоторые измерения в короткие промежутки времени либо отсутствуют во время работы устройства, либо дают аномальные пики в выключенном состоянии. По этой причине в [2] предложили, помимо порога мощности, рассматривать также и порог времени. При этом порог мощности фиксируется с помощью вышеизложенных методов или выбирается эмпирически вручную, как это сделано в [1], а под порогом времени (ц0¹⁾,ц1¹⁾) понимается минимальное время, в течение которого устройство I должно находиться в заданном состоянии. Например, если последовательность измерений мощности ниже А¹ в течение времени t < р,^, то считается, что эта последовательность находится в предыдущем состоянии (включено в данном случае).

(д01),д11)^ подбирался эмперически вручную и фикси ровался, но также указывалось на возможность его оптимизации с помощью минимза-I)

ции среднеквадратичного отклонения между исходным сигналом Р3 и восстановленным.

Восстановленный сигнал по порогам определялся следующим образом:

р ⁽¹⁾ _ ^r ON ^—

Nt • тгагп

^N trai

Е

3=1

L out

— Е 8^ р¹-

Lout ^ зг 3,г г=1

^N train        ^L out

р(1)   = rOFF

д= Е £ Е (1 - ^

3 = 1

(1)   р(1) О(1)     р(1)(1)

BP3 — r0N s3 + rOFF(1  s где BP.1) — восстановленный сигнал для сегмента j l-го устройства, Ntтaгn ~ размер обучающей выборки, Lout — длина выходной последовательности, a s^, Г.г — определены выше. Обоснование выбора такого функционала приведено в [1]. Порог времени (тО1),т11)) можно рассматривать как некоторый гиперпараметр и использовать соответствующие инструменты для его оптимизации. Одним из наиболее современных фреймворков для автоматического подбора гиперпараметров является Optuna. Она оказывается эффективнее полного перебора, а также подобных по функционалу библиотек. В данной статье используется фреймворк Optuna [4]. Параметры перебора указаны в табл. 1.

Таблица 1

Параметры перебора временного порога

Устройство	Т о	Т 1	Количество запусков
Стиральная машина	[1;10]	[10; 50]	100
Посудомоечная машина	[10; 50]	[10; 50]	200
Холодильник	[1;10]	[1;10]	50

Для каждого эксперимента модели обучались пять раз до сходимости на валидационной выборке. Результаты на тестовоый части усреднялись.

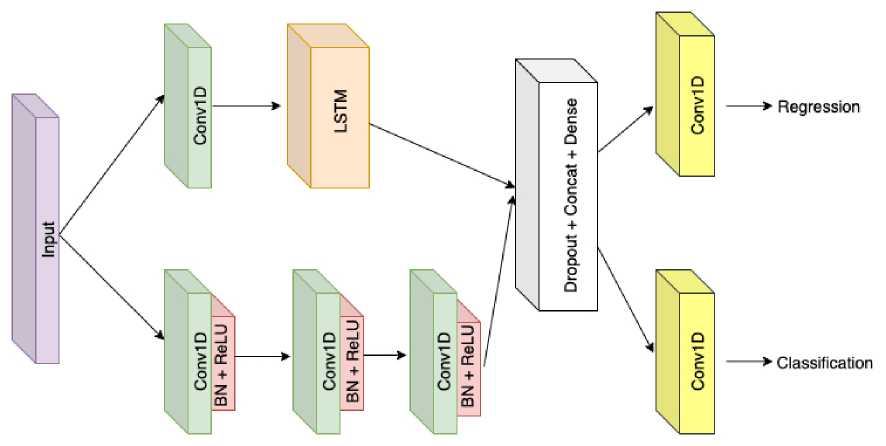
Рис. 1. Предложенная архитектура.

• 5.    Сравнение результатов

Полученные в ходе экспериментов с предложенной архитектурой нейросети результаты представлены в табл. 2-4.

В табл. 2 приведены результаты сравнения метрики МАЕ между исходным и восстановленным сигналом для разных устройств и методов нахождения порога. Можно заметить, что подбор временного порога, позволил улучшить значение целевой метрики.

Таблица. 2

Сравнение метрики качества МАЕ между исходным и восстановленным сигналом

Методы вычисления порогов	Посудомоечная машина	Холодильник	Стиральная машина.
МР	3.48	4.67	3.96
VS	4.39	4.71	6.60
АТ	26.37	4.66	7.42
АТ с подобранными (нАА	19.48	4.66	6.79

В табл. 3 приведены результаты применения разработанной модели для задачи классификации. В целом она. дает значительно более хорошие результаты по сравнению с моделью GRU и результаты близкие к данным модели CONV.

Таблица 3

Сравнение метрики качества F i для различных моделей

Порог активации	Модель	Посудомоечная машина	Холодильник	Стиральная машина
МР	CONV	0.93	0.87	0.93
	GRU	0.84	0.87	0.87
	Предложенная модель	0.90	0.86	0.96
VS	CONV	0.93	0.87	0.88
	GRU	0.84	0.87	0.82
	Предложенная модель	0.90	0.86	0.89
АТ	CONV	0.91	0.86	0.97
	GRU	0.90	0.86	0.96
	Предложенная модель	0.90	0.89	0.93
АТ с подобранными aw	CONV	0.93	0.86	0.97
	GRU	0.91	0.86	0.97
	Предложенная модель	0.94	0.89	0.94

В табл. 4 приведены результаты работы предложенной модели в задаче регрессии. Блочная архитектура на основе рекуррентных и сверточных нейронных сетей позволила улучшить результаты целевых метрик независимо от типа устройства.

Таблица 4

Значение метрики МАЕ для задачи регрессии

Модель	Посудомоечная машина	Холодильник	Стиральная машина
CONV	11.59	26.95	18.25
GRU	8.07	28.68	15.00
Предложенная модель	7.78	26.06	14.43

• 6.    Заключение

В данной работе предложена новая архитектура нейронной сети, включающая параллельные блоки на основе рекуррентных и сверточных сетей, для решения задачи дезагрегации данных об энергопотреблении типовых приборов домохозяйств, которая оказалась более универсальной и эффективной по сравнению с архитектурами CONV и GRU при решении задачи регрессии и близкой по результатам к уже известной архитектуре CONV по метрике Fi.

Была также исследована возможность оптимизации временных порогов для последующего использования найденных параметров для выбора порогов активации. Найденные параметры оказались оптимальными с точки зрения сравнения среднеквадратичного риска между исходным и восстановленным временным рядом.

При проведении дальнейших исследований планируется изучение возможности применения разработанных методов и архитектуры нейронной сети для других типов энергопотребителей, включая промышленные энергоустановки.