О построении показателя качества функционирования Сберегательного банка РФ

В процессе функционирования различных финансовых институтов возникает потребность в оценке их «успешности». Состояние эффективного и безопасного (с позиции экономики) функционирования предприятия может быть оценено с помощью специальных средств: индексов, показателей, критериев оценки. Но, как показывает практика, большое число учитываемых критериев и их многообразие приводит к необходимости построения обобщенного показателя качества, отражающего состояние данного института и целесообразность его функционирования.

Практическую составляющую рассмотрим на примере банков: для описания функционирования банков используются различные индикаторы. В качестве таких индикаторов в работе будут рассмотрены отчет о соблюдении обязательных нормативов (форма 135), представляющий собой численную информацию о выполнении или невыполнении организацией какого-либо норматива, и активы нетто - балансовый показатель отчетности, определяемый как разница между стоимостью имущества компании и суммой её обязательств.

В работе рассмотрен Сберегательный банк РФ с действующей лицензией. Задача заключается в построении агрегированных индексов «качества» с помощью методов Томсона на основе 135 формы.

Метод оценки Томсона.

Математически задача построения сводного по нескольким показателям индекса заключается в следующем: необходимо найти коэффициенты линейной регрессии по нескольким независимым и одному зависимому фактору. Однако в данной проблеме отсутствует результирующая компонента, поэтому применение обычных статистических методов, например МНК, невозможно.

Из критерия триад Спирмена известно, что 2 и 3 показателя можно описать одним генеральным фактором [3]. Однако для большего числа показателей необходимо выполнение определенных условий. Опишем их для случая одного генерального фактора и четырех показателей. Рассмотрим матрицу корреляции при n=1 и m=4:

hi   rn   Г13

^ _ r21   h2   Г23

r31   r32   h3

_ r4i   r42   r43

Ранг этой матрицы равен единице, если все миноры второго порядка равны нулю. Выбрав миноры, в которые входит лишь по одному значению общности, выпишем ряд уравнений относительно всех общностей. Например, h12 может быть вычислен с помощью любого из следующих трех h2 r           h2   r           h2   r                    r r уравнений: [ 1    13] = 0, [ 1    14] = 0, [ 1    14] = 0 или h12 = 12 13 = r21   r23         r21   r24         r31 r34                    r23

r 12 r 14     r 13 r 14

^r 24         ^r 34 ^.

Исключив h12,получим известный критерий тетрад Спирмена [5].

Таким образом, мы определили условия, которым должны удовлетворять исходные данные для того, чтобы их можно было описать одним генеральным фактором.

Однако, возможна такая ситуация, что подобные условия не выполнены или что несколько переменных невозможно будет описать одним латентным фактором. В таком случае используется выделение факторов методом максимального правдоподобия. Такой способ дает разбиение исходных данных на группы, в которых уже выполняется критерий тетрад Спирмена.

Далее нам потребуется инструмент для нахождения этих латентных переменных.

В данной статье предлагается определять коэффициенты по методу Томсона. Для начала выпишем основное уравнение факторного анализа:⃗X⃗ = AF, где A - матрица факторных нагрузок, F - вектор латентных (общих) факторов, X - p-мерный вектор показателей [1].

Метод Томсона рассматривает данную модель как бы

«вывернутой наизнанку», а именно как регрессию зависимых переменных Гн,...,Гр) по аргументамx(1), _,x(p). Тогда коэффициенты cij из уравнения F = CX, где C -матрица коэффициентов cij, находят в соответствии с методом наименьших квадратов из условия n p′          p                     n p′          p

∑∑(fv(i)-∑cijxv(j))2=mciijn∑∑(fv(i)-∑cijxv(i)) v=1 i=1        j=1                 v=1 i=1        j=1

Поскольку решение данной экстремальной задачи выписывается в терминах ковариации x(i) и f(j), то отсутствие наблюдений по зависимым переменным f(j) можно компенсировать знанием их ковариаций, так как

x(1)

А

легко посчитать, что E

x (p) _f(1)

(x(1),…,x(p),

f(1),…,f(p′))  =(

AAT + V A

AT      Ip′

),

⎩⎣f(p′)⎦

где V - матрица остаточных дисперсий.

Отсюда, используя известные формулы метода наименьших квадратов, получаем

F = ( I + AtV-1A)-1AtV-1X.

При подстановке в последнее выражение последовательно значений векторов наблюдаемых показателей, мы получим оценки агрегированного индекса [1].

Применение метода Томсона для построения показателя качества функционирования Сберегательного банка РФ.

Для исследования была взята информация, полученная из 135 формы банковской отчетности, взятой за период с сентября 2013 по апрель 2015 (данные считываются ежемесячно). Обязательные нормативы – это количественные ограничения деятельности банка, которые должны обеспечить [2]:

• •    достаточность собственного капитала

• •    ликвидность банков

• •    высокое качество активов

Были составлены исходные таблицы данных, состоящие из следующих характеристик, наблюдающихся ежемесячно [4]:

• 1.    Н1.0  – норматив достаточности капитала; ограничивает

• 2.    Н1.1 – норматив достаточности основного капитала банка (≥ 4.5)

• 3.    Н10.1 – норматив совокупной величины риска по инсайдерам банка; ограничивает совокупный кредитный риск банка в отношении всех физических лиц, способных воздействовать на принятие решения о выдаче кредита банком (≤ 3)

• 4.    Н12 – норматив использования собственных средств банка для приобретения акций (долей) других юридических лиц; жестко ограничивает размеры вложений банка в акции других компаний (≤ 25)

• 5.    Н2 – норматив мгновенной ликвидности; ограничивает риск потери банком ликвидности в течение одного операционного дня и определяет минимальное отношение суммы высоколиквидных активов банка к сумме обязательств банка по счетам до востребования, скорректированных на величину минимального совокупного остатка средств по счетам физических и юридических лиц (кроме кредитных организаций) до востребования (≥ 15)

• 6.    Н3 – норматив текущей ликвидности; характеризует риск потери ликвидности банком в краткосрочном периоде (30 дней) и определяет минимальное отношение суммы ликвидных активов банка к сумме обязательств банка по счетам до востребования и со сроком исполнения обязательств в ближайшие 30 календарных дней (≥ 50)

• 7.    Н4 – норматив долгосрочной ликвидности; характеризует риск потери банком ликвидности в результате размещения средств в долгосрочные активы (≤ 120)

• 8.    Н7 – м; ограничивает долю крупных кредитов в кредитном портфеле банка. Крупные кредиты могут превышать капитал банка в 8 раз. (≤ 800)

• 9.    Активы нетто – балансовый показатель отчетности, определяемый как разница между стоимостью имущества компании и суммой её обязательств.

возможности роста банка без увеличения капитала банка (≥ 10)

Так как вычисляемая характеристика векторная, ее размерность зависит от размерности пространства общих факторов. Соответственно, для вычисления требуемого агрегированного индекса размерность пространства общих факторов должна равняться 1. Это выполняется при условии равенства нулю всех миноров второго порядка редуцированной корреляционной матрицы.

Проверяем выполнение критерия тетрад Спирмена:

Table 1

7 12 7 13 723	7 12 ^ 14 7 24	7 12 7 15 7 25	7 12 7 16 726	7 12 7 17 727	712718 728	712719 729
0,316935	2,74297	1,897183	4,82666	1,238475	1,10402	2,098518

Как видим, уже на первой общности критерий тетрад не выполнен.

Применяя метод максимального правдоподобия, мы выделяем 2 фактора:

Table 2

	Фактор 1	Фактор 2
H1.0	0,933202	-0,330702
H1.1	0,481088	-0,346951
H10.1	0,029582	0,780007
H12	-0,763423	0,197113
H2	-0,783136	-0,587934
H3	-0,604576	-0,783972
H4	0,489373	0,153825
H7	-0,941262	-0,057430
Активы т.р	-0,907257	-0,023242

Разобьём данные на две группы и вычислим оценки общностей методом тетрад.

Table 3

^ 1	0,961	0,854	0,880	0,853
^ 2	0,738	0,629	0,647	0,797
^ 2	0,303	0,493	0,370	0,456
^ 4	0,676	0,886	0,717	0,764
^ 2	0,847	0,782	0,912	0,899

Значения вычисленных оценок примерно близки, проверим миноры второго порядка. Для удобства представим их в виде таблицы.

Table 4

0,0008	-0,0075	0,0086	-0,0016
-0,0075	0,0058	0,0021	-0,0061
0,0086	0,0021	-0,0058	-0,0029
-0,0016	-0,0061	-0,0029	0,0032

Вычисляя определители корреляционной матрицы, находим, что они близки к нулю – матрицы могут быть плохо обусловленными, т.е. близкими к вырожденности. Но как определить, насколько миноры второго порядка близки к нулю? Предположим проверку числом обусловленности: cond(A) = ||A| * ||A^-1|, где ||A| = ^max j ||^a j || (^ j — 7—ый столбец матрицы). Если 1 < cond(A) <100, матрица считается хорошо обусловленной.

Проверяя матрицу, соответствующую максимальному по модулю значению из таблицы 4, обнаруживаем, что ее число обусловленности равно 317,62, можем сказать, что матрица близка к вырожденности, следовательно, данные лежат в пространстве одного общего фактора. Таким образом, во всех рассматриваемых случаях мы можем описать данные одним агрегированным индексом.

Получаем индексы с помощью метода Томсона для первого и второго фактора. Результаты представлены в Таблице 5.

Table 5

индекс 1 фактора	индекс 2 фактора
1,6783855	-0,5533021
3,0274307	0,4093662
3,1022959	0,5103972
1,2388174	0,0403007
0,7020337	-0,3564170
0,4031139	0,1320736
-0,1727468	0,1757580
0,0067733	-0,1643163
-0,0750622	-0,1089598
-0,1887816	-0,2547105
-0,4309927	0,1529852
-0,7747518	0,1429862
-0,7074786	0,1052887
-0,9139861	-0,4130190
-0,8706791	-0,2093949
-1,2028018	0,5098653
-1,0873486	-0,0372981
-1,1977530	-0,1026844
-1,2703923	-0,0474838
-1,2660750	0,0685648

Представим в виде графика.

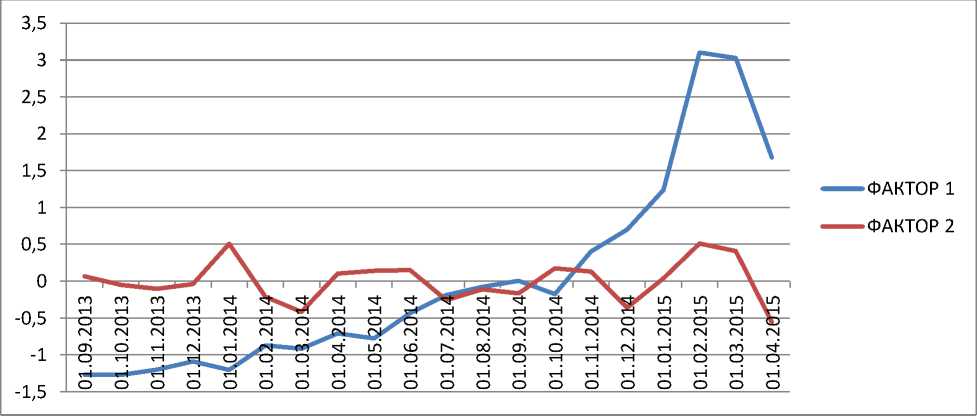
Соотнося полученные результаты и исходные данные, можем прийти к выводу, что построенный индекс говорит о благополучии банка: в целом наблюдается положительная динамика, которая свидетельствует о хорошем качестве функционирования банка, кратковременные спады можно объяснить ухудшением некоторых нормативов. Например, при самом выраженном спаде, проявляющемся с 01.03.2015 по 01.04.2015, значительно снизились активы банка вкупе с нормативом мгновенной ликвидности и нормативом максимального размера крупных кредитных рисков.