О построении поверхности текучести стали 45 и проверке постулата изотропии на прямолинейных траекториях при многократных знакопеременных нагружениях

Построение поверхности текучести в теории течения имеет функциональное значение для ее практических приложений. Начальное положение поверхности текучести в девиаторном пространстве напряжений соответствует сфере Мизеса. В процессе нагружения она изотропно расширяется и одновременно изменяет свою форму. На практике при построении различных математических моделей теории течения зачастую ее приближенно считают расширяющейся сферой, что нередко приводит к хорошим результатам. Вопрос о достоверности такого предположения вызвал необходимость ряда экспериментальных исследований для различных конструкционных материалов по установлению зависимости радиуса гипотетической сферической поверхности текучести от длины дуги траектории пластического деформирования. Первые систематические экспериментальные исследования бы- ли проведены Г.Б. Талыповым, Р.А. Арутюняном, Ю.Г. Коротких [1-3]. Для различных конструкционных материалов установлено, что при переходе материала из упругого состояния в пластическое при простых лучевых нагружениях радиус гипотетической поверхности может либо сразу возрастать, либо сначала временно уменьшаться с последующим возрастанием. Причина этого кроется в структурном изменении материалов и развитии деформационной анизотропии в процессе пластического деформирования. Экспериментальное разрешение этой проблемы необходимо для обоснованного построения математических моделей пластического деформирования.

1.    Основные положения

В теории процессов упругопластического деформирования тензоры напряжений и деформаций представляют [4-6] в виде суммы шаровых тензоров и тензоров-девиаторов:

T = ( о j = G o ( 3 j +о ( S j ), Т = ( е j = Е о ( 3 j ) + Э(Эу), ( i , j = 1,2,3), (1)

где 5 ij - символ Кронекера;

• ^О 0 = 3 ^O ij ⁵ ij , ^е 0 = 3 ^e ij ⁵ ij , ^О = л] S ij S ij , ^Э = V ^Э ij^Э j , ⁽ i , ^j = 1, ²,^{3)     (2)}

• -    модули шаровых тензоров (средние напряжение и деформация) и тензоров девиаторов соответственно;

S ij =O j -5 j O о , Э , -е ,j -5 i, е о , S i = S j , Э * = ЭЭ, (и - 1,2,3) (3)

• -    компоненты девиаторов и направляющих тензоров напряжений и деформаций соответственно.

В случае простого пропорционального нагружения направляющие тензоры напряжений и деформаций совпадают, то есть ( S * ) = (Э * ), и для начально-изотропных материалов с учетом упругости объемной деформации связь между тензорами в физическом пространстве имеет вид

О о = 3 K е „ , S ij = j Э j = 2 G p Э j , ( i,j = 1,2,3) ,            (4)

где K - модуль объемной упругости; G p - пластический модуль сдвига. В качестве закона упрочнения материалов для любого сложного напряженно-деформированного состояния принимается универсальная единая диаграмма деформирования Роша и Эйхингера а = Ф(Э) .

При сложном нагружении направляющие тензоры напряжений и деформаций, а также их скоростей не равны между собой, то есть ( S * ) ^ (Э * ), ( S * ) ^ (Э * ), и тензорам напряжений и деформаций в линейном шестимерном евклидовом пространстве E ₆ ставятся в соответствие векторы напряжений и деформаций

S = S 0 + _S , S 0 = S _o i o , ₅ = S k i k , _n - _n „ - , ^{( k} ^Д.-⁵),          ⁽⁵⁾

£=£0 + Э, £0 = Эoio, Э = Эк i k, где S0, £0 - векторы напряжений и деформаций в одномерном подпространстве объемного растяжения и сжатия с гидростатической осью, направление которой характеризуется единичным вектором i0;

• о , Э - векторы напряжений и деформаций формоизменения в пяти

мерном девиаторном подпространстве E5; {iк} - фиксированный ко ординатный базис А.А. Ильюшина к которому отнесено E5 [4-6],

<

S 0 = . Vi. S 1 = ^ S 11, S 2 = V2 f S 22 + 2 S 11 '

s ₃ = VI s ₁₂ , s ₄ = VI s ₂₃ , s ₅ = VI s ₁₃ ,

Э 0 =     . Э , = ЦЭ _и, Э 2 = V2 ( Э 22 + 2 Э 11

Э ₃ = |2Э₁₂, Э ₄ = |ЭI ₂₃ , Э ₅ = ^Э ₁₃

,

,

• - компоненты (координаты) векторов напряжений и деформаций соответственно.

Модули векторов в пятимерном подпространстве E5 равны модулям тензоров-девиаторов напряжений и деформаций соответственно а = TSkS; = SiSSS,, Э = ТЭкЭ; = ЭЭЭЭ", (к = 1,2,...5), (i,j = 1,2,3). (7)

Определяющие соотношения теории процессов для плоских траекторий имеют вид [6]

dS_k      Э* ( d о „

<

"=M = ^M 1 = + |чГ- ^M i ^cos ^ 1 I~, ( k = 1,2,3), ds ds V ds / о

d^i       Mi

—^{1 +K} i = ^{i s}m ^ i ,

I ds         о где s - длина дуги траектории деформирования; ^1 - угол сближения вектора напряжений σ с касательной к траектории деформирования;

d о

- функционалы ds

K i - кривизна траектории деформирования; M 1

пластичности.

В теории течения В. Прагера [6, 7-9] принимают M 1 = 2 G , и деформации в E ₅ разлагают на упругие Э ^e и пластические Э ^p части, а напряжения на активные напряжения σ ⁰ и добавочные остаточные микронапряжения a :

dЭ = dЭe + dЭp =—+dЭp, o = о 0 + a, 2G где G - упругий модуль сдвига материала. Определяющие соотноше- ния имеют вид dЭ = do^+d ^ grad f , если do • grad f > 0,

<

2 G

d3 = d3^e = -^⁶- , если do • grad f <  0,

2G где dX = dsp - приращение дуги sp траектории пластического деформирования; f (σ, Эp) - функция нагружения, описывающая в E5 гипотетическую поверхность текучести Прагера, которая разделяет области активного пластического деформирования и упругой разгрузки. При упругой разгрузке поверхность текучести остается неизменной.

Все математические модели теории течения, основывающиеся на понятии поверхности текучести, отличаются ее формой. Обычно на практике ее считают сферой, которая может изменять свои размеры и местоположение при неизменной форме (трансляционно-изотропное упрочнение):

2 f = ( 6 - a) • ( 6 - a) - C * ( s^p ) = 0, (11) где C p ( s p ) = о ⁰ - скалярная функция изотропного упрочнения, зависящая от длины дуги траектории пластического деформирования s p и равная радиусу поверхности текучести. При s p = 0 радиус гипотетической начальной поверхности текучести о ⁰ = о ^т = V2/3 о _т, где о _т -начальный предел текучести при простом нагружении, определяемый по техническому допуску на остаточную деформацию. За такой допуск при растяжении в теории пластичности, как правило, принимают Г * = 0,2% = 2 - 10 — ³ (Э * = 0,245%). При данном допуске на остаточную деформацию на основании постулата изотропии начальная поверхность текучести в девиаторном подпространстве E ₅ для начально изотропных тел соответствует сфере Мизеса. Установлено, что при меньших допусках на остаточную деформацию очертание сферы Мизеса может искажаться и терять свою форму [8]. На девиаторной плоскости окружность Мизеса и вписанный в нее шестиугольник Сен-Венана приобретают тройную симметрию [10]. Однако вследствие развития деформационной анизотропии в процессе нагружения поверхность текучести может вытягиваться в направлении развития процесса [6, 7].

В качестве закона упрочнения при сложном нагружении по траекториям малой и средней кривизны используется закон Одквиста-Ильюшина о = Ф( s) (12)

с параметром прослеживания процесса s >  Э. Использование диаграммы (12) позволяет учесть эффект Баушингера, реализуемый при простых знакопеременных разгружениях.

В данной работе рассматривается эффект Баушингера при простых знакопеременных разгружениях-догружениях, которые периодически повторяются через специально подобранные равноотстоящие точки диаграммы (12). В каждой точке излома траектории K начала разгрузки при значении нового предела текучести о K эффект Баушингера оценивался безразмерным параметром [1, 11, 12]

^e=° м| / ^о К                         ⁽¹³⁾

при соответствующей величине дуги траектории sp пластического деформирования. Здесь аМ - вторичный предел текучести при разгрузке из точки K при «протыкании» поверхности текучести в точке М по диаметральному направлению, который определялся по допуску на остаточную деформацию Э* . В этом случае радиус текущей изменяющейся сферической поверхности текучести о0 = Ср(sp)=2 (о K —°М),                  (14)

а смещение ее центра относительно начала координат а = оK -Ср = 2(аK +оМ).                (15)

2. Экспериментальные исследования

Экспериментальные исследования проводились в опытах при знакопеременном нагружении-разгужении на автоматизированном испытательном комплексе на сложное нагружение СН-ЭВМ имени А.А. Ильюшина в лаборатории механических испытаний кафедры «Сопротивление материалов, теории упругости и пластичности» Тверского государственного технического университета. Опыты реализовывались на цилиндрических тонкостенных образцах из стали 45 в состоянии поставки с площадкой текучести, которые имели стенки толщиной h = 1 мм, радиус срединной поверхности поперечного сечения R = 15,5 мм и длину рабочей части l = 110 мм. В испытании по программе № 1 образец подвергался многократному знакопеременному нагружению через равные приращения по растяжению А Э 1 = 0,5% (рис. 1), с последующим знакопеременным нагружением на |АЭ 1| = 0,75% при сжатии [13]. В аналогичном испытании по программе № 2 образец подвергался многократному нагружению при кручении с приращениями А Э 3 = 0,5% (рис. 2) и последующим знакопеременным нагружением на |АЭз| ~ 0,75%. В среднем опыты в режиме непрерывного деформирования образцов с постоянной скоростью

£ = 10 ⁶ с ¹ продолжались в течение 8-9 часов. В испытании на кручение всю запланированную траекторию осуществить не удалось, поскольку образец несколько ранее потерял устойчивость.

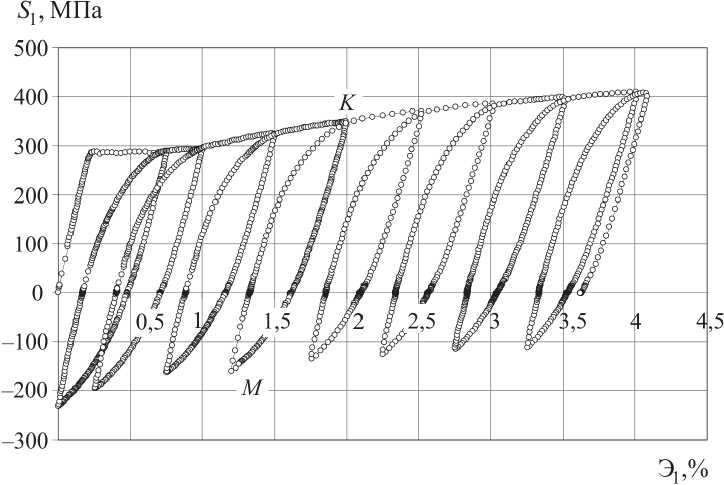
Рис. 1. Программа № 1. Локальная диаграмма знакопеременного нагружения при растяжении-сжатии S ₁ - Э ₁

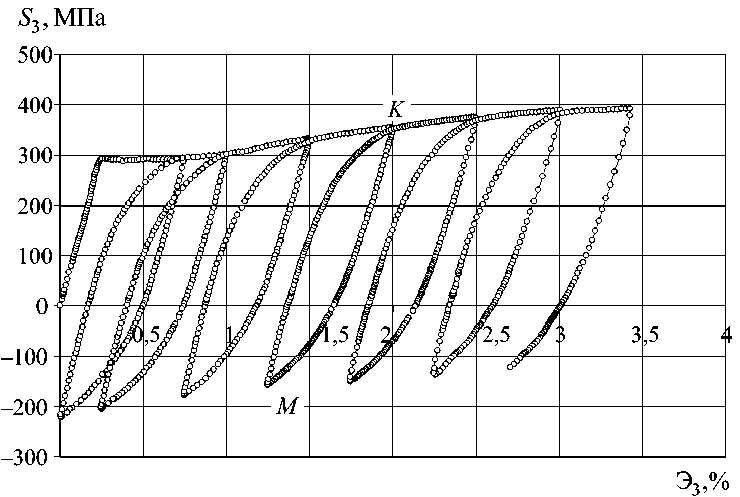
Рис. 2. Программа № 2. Локальная диаграмма знакопеременного нагружения при кручении S ₃ - Э₃

На рис. 3 приведены полученные на основе обработки экспериментальных данных осредненные зависимости параметра β , характеризующего эффект Баушингера, от длины дуги траектории пластического деформирования sp , на рис. 4 – изменение радиуса σ0 гипотетической сферической поверхности текучести, а на рис. 5 – смещение центра гипотетической сферической поверхности текучести. На этих рисунках затушеванные экспериментальные точки соответствуют опыту при растяжении-сжатии, белые – при кручении. Представленные на рис. 3–5 зависимости построены при четырех различных допусках на остаточную деформацию при определении вторичных пределов текучести при растяжении е* = (0,2; 0,15; 0,01; 0,05)%, что в подпространстве E5 соответственно составляет Э* = (0,245; 0,18325; 0,1225; 0,06125)%. При кручении данный допуск у * на остаточную сдвиговую деформацию при зависимости Э3 = V2 £12 = Y/72, где y= 2е12, равен V23p и составлял соответственно 0,346; 0,259; 0,173; 0,087 %.

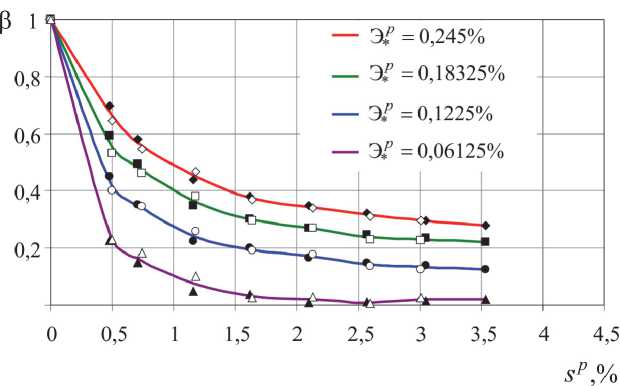
Рис. 3. Изменение коэффициента β от s^p , характеризующего эффект Баушингера

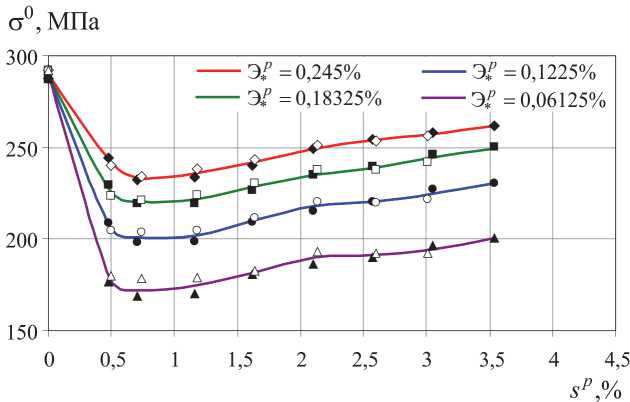
Рис. 4. Изменение радиуса гипотетической поверхности текучести

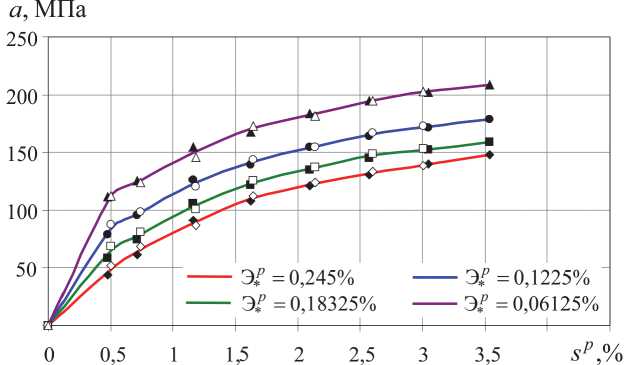
Рис. 5. Смещение центра гипотетической поверхности текучести

Из полученных диаграмм видно, что с ростом допуска на остаточную деформацию радиус поверхности текучести о 0 увеличивается, а смещение ее центра а уменьшается . Максимальное отклонение для рассмотренных крайних допусков на остаточную деформацию E *p = 0,2% и E * p = 0,05% для радиуса о ⁰ гипотетической поверхности текучести составляет примерно 45 % (см. рис. 4), а для смещения ее центра – примерно 55 % (см. рис. 5). При максимально достигнутых уровнях пластической деформации s ^p в эксперименте значения параметра a для всех рассмотренных допусков на остаточную деформацию не превзошли значения начальных пределов текучести о т . Таким образом, центры текущих поверхностей находились внутри начальной поверхности текучести. При этом чем меньше допуск на остаточную деформацию, тем существенней влияние смещения центра поверхности текучести. Если взять отношение

a _ 1 -в r 1 + в ,

которое напрямую зависит только от параметра в , то при максимально достигнутых уровнях пластической деформации s^p при допуске E * p _ 0,2% оно составляет 0,55 , а при допуске E * p _ 0,05% равно 0,98 .

Проведенные экспериментальные исследования по многозвенным траекториям при знакопеременном нагружении-разгружении позволяют проверить постулат изотропии А.А. Ильюшина [5, 14, 15], ко- торый проверялся многими авторами по различным программам деформирования на разных материалах [16–22]. Траектория деформирования по программе № 2 может быть получена путем вращения траектории по программе № 1 на угол 90 градусов в плоскости Э1- Э3. Для проверки выполнения постулата изотропии для обеих траекторий построены совмещенные глобальные диаграммы деформирования σ-Э (рис. 6), на которых видно что экспериментальные диаграммы обеих траекторий с достаточной степенью точности совпадают между собой.

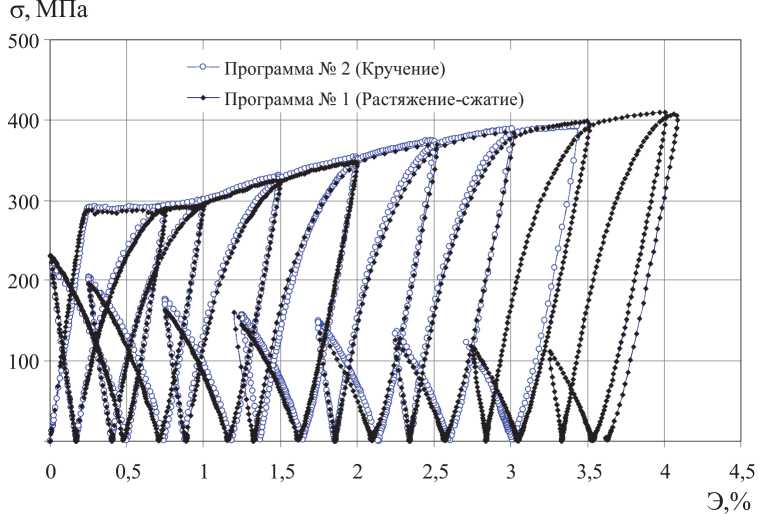
Рис. 6. Программы № 1 и 2. Глобальные диаграммы σ- Э

Заключение

По результатам проведенных экспериментальных исследований и их обработки, а также исследований на других материалах [23, 24] можно сделать следующие выводы.

• 1.    Эффект Баушингера для стали 45 сопровождается уменьшением по модулю вторичного предела текучести σ т М и параметра β на начальном локальном участке процесса деформирования после излома с ростом длины дуги s^p . Параметр β при различных допусках на остаточную деформацию стремится к некоторому стационарному значению при s^p >  (3...4)% .

• 2.    С ростом допуска на остаточную деформацию Э*⁷ параметр в увеличивается и для общепринятого допуска e ^p = 0,2% (Э * = 0,245%) составляет примерно 0,3 при достигнутом уровне s^p .

• 3.    Радиус гипотетической поверхности текучести о ⁰ = C _p ( s^p ) с ростом s ^p испытывает временное понижение типа «нырка» и с ростом допуска на остаточную деформацию до е ** = 0,2% приближается по своей форме к сфере. При этом отклонение радиуса при крайних значениях допуска на остаточную деформацию достигает 45 %.

• 4.    Временное уменьшение о ⁰ = C _p ( s^p ) связано с изменением внутренней структуры материала на мезоуровне, изменением ориентации микронапряжений с ростом деформаций, но не с его разгрузкой. В каждый момент нагружения по внутренней структуре – это уже другой материал с иными механическими характеристиками [25].

• 5.    Отклонения параметра смещения центра предельной поверхности a ( s^p ) для рассмотренных различных допусков на остаточную деформацию при определении пределов текучести достигают 55 %.

• 6.    В некоторых математических моделях теории течения уменьшение радиуса гипотетической сферической поверхности текучести о ⁰ = C _p ( s^p ) не только при простом, но и сложном нагружении связывают не с изменением структуры материала на мезоуровне и ориентацией микронапряжений, а с упругим разупрочнением начальноизотропного тела, ошибочно полагая при этом скорость деформирования s^p<  0, что невозможно, так как s и s всегда положительны.

• 7.    Для реализованных типов траекторий многократного нагруже-ния-разгружения с изломами на 180 градусов постулат изотропии по скалярным свойствам выполняется достаточно хорошо. Что касается векторных свойств, то они выполняются в рамках точности теории простых процессов.