О поверхностях памяти, разделяющих процессы монотонных и циклических нагружений
Автор: Бондарь В.С., Абашев Д.Р.
Статья в выпуске: 3, 2022 года.
Бесплатный доступ
Процессы упругопластического деформирования конструкционных материалов могут состоять из последовательности монотонных и циклических режимов нагружения, при которых возникают своеобразные эффекты и особенности. Математическое моделирование таких процессов, а также оценка и прогнозирование ресурса представляют собой весьма сложную задачу. К тому же анализ переходных процессов от циклического к монотонному и от монотонного к циклическому показывает необходимость разделения этих процессов. На основе анализа результатов экспериментальных исследований образцов из нержавеющей стали 12Х18Н10Т при жестком (контролируемые деформации) процессе деформирования, представляющим собой последовательности монотонных и циклических режимов нагружения, в условиях одноосного растяжения-сжатия при нормальной температуре выявлены особенности и различия процессов монотонных и циклических нагружений. Для описания этих особенностей и разделения процессов монотонных и циклических режимов нагружения в теориях пластического течения при комбинированном упрочнении вводятся различные варианты поверхностей памяти. Анализ результатов экспериментальных исследований нержавеющей стали показал, что в пространстве тензора пластических деформаций размер поверхности памяти определяется размахом пластических деформаций, а положение центра - значениями средних пластических деформаций при циклическом нагружении. Рассмотрены различные варианты поверхности памяти, выявлены их возможности и недостатки и определен наиболее адекватный вариант поверхности памяти. Для подтверждения работоспособности этого варианта поверхности памяти совместно с уравнениями модели пластичности Бондаря проведено сравнение расчетных и экспериментальных результатов и получено надежное соответствие этих результатов как по кинетике напряженно-деформированного состояния, так и по числу циклов до разрушения.
Пластическое деформирование, поверхность памяти, монотонные и циклические нагружения, расчет и эксперимент, число циклов до разрушения
Короткий адрес: https://sciup.org/146282549
IDR: 146282549 | УДК: 539.374 | DOI: 10.15593/perm.mech/2022.3.05
Текст научной статьи О поверхностях памяти, разделяющих процессы монотонных и циклических нагружений
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2022PNRPU MECHANICS BULLETIN
Нестационарные и несимметричные процессы циклического деформирования состоят из последовательности монотонных и циклических режимов нагружения, при которых возникают своеобразные эффекты посадки и вышагивания (ratcheting) петель пластического гистерезиса. Математическое моделирование таких процессов в условиях жесткого (контролируемые деформации) и особенно мягкого (контролируемые напряжения) нагружений, а также оценка и прогнозирование ресурса представляют собой весьма сложную задачу. К тому же анализ [1–17] переходных процессов от циклического к монотонному и от монотонного к циклическому показывает необходимость разделения процессов монотонного и циклического деформирования. Для этого в пространствах тензора микронапряжений или тензора пластических деформаций или других пространствах вводится поверхность памяти, что разделяет циклические и монотонные процессы деформирования [1–17].
Математическое моделирование таких процессов деформирования и накопления повреждений строится в основном на вариантах теорий пластичности [1–41], относящихся к классу теорий пластического течения при комбинированном (изотропном и анизотропном) упрочнении. В настоящей работе математическое моделирование процессов деформирования и накопления повреждений базируется на варианте теории пластичности – модели Бондаря [19], который, как показано в работах [39–41], является наиболее адекватным вариантом описания процессов деформирования и разрушения при циклических нагружениях по сравнению с моделями Коротких [1–8] и Шабоша [10; 20; 23; 27].
В настоящей работе на основе анализа результатов экспериментальных исследований выявлены особенности эволюции поверхности памяти при различных последовательностях монотонных и циклических режимов нагружения. Рассмотрены различные варианты поверхности памяти, выявлены их возможности и недостатки и определен наиболее адекватный вариант поверхности памяти, разделяющий процессы монотонного и циклического нагружений.
Для подтверждения работоспособности варианта поверхности памяти совместно с уравнениями варианта теории пластичности – модели Бондаря, проведено сравнение расчетных и экспериментальных результатов исследований нержавеющей стали 12Х18Н10Т при жестком нагружении, состоящем из последовательности монотонных и циклических режимов нагружения. Сравнение проводится по кинетике напряженно-деформированного состояния, размаху и среднему напряжению цикла в процессе этапов циклических нагружений, а также по числу циклов до разрушения.
1. Эксперимент
Рассматриваются экспериментальные исследования цилиндрических образцов нержавеющей стали 12Х18Н10Т. Химический состав и механические свойства представлены в таблице.
Химический состав и механические свойства стали 12Х18Н10Т
Chemical composition and mechanical properties of steel 12Х18Н10Т
|
C |
Si |
Mn |
Ni |
S |
P |
Cr |
Cu |
Ti |
Fe |
|
<0,12 |
<0,8 |
<2 |
9–11 |
<0,02 |
<0,035 |
17–19 |
<0,3 |
0,4–1 |
~67 |
|
σ 0,2 , МПа |
σ в , МПа |
δ 5 , % |
ψ , % |
KCU, Дж/см2 |
|
225–315 |
550–650 |
46–74 |
66–80 |
215–372 |
Испытания проводятся на универсальной испытательной машине Zwick Z100. Геометрия и размеры испытываемых образцов соответствуют требованиям стандарта ASTM E606. Диаметр рабочей части образца 8 мм, длина рабочей части образца 24 мм, радиус перехода от рабочей к захватной части 32 мм (рис. 1).
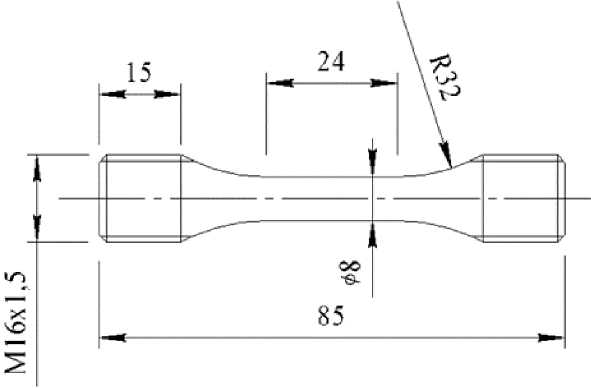
Рис. 1. Образец для испытаний по ASTM E606
Fig. 1. Test specimen according to ASTM E606
Деформация в процессе испытаний измеряется и контролируется по навесному экстензометру с измерительной базой в 10 мм. Погрешность измерения осевой силы составляет 1 % и осевого перемещения – 1 %. Реализуется жесткое нагружение, т.е. нагружение при задаваемом значении изменения осевой деформации. Деформирование образца осуществляется при комнатной температуре со скоростью, равной 0,5 % с–1 при монотонном нагружении, и частотой 0,2 Гц – при циклическом нагружении.
2. Монотонные и циклические нагружения нержавеющей стали 12Х18Н10Т
Рассматриваются результаты двух экспериментальных исследований нержавеющей стали 12Х18Н10Т при одноосном жестком нагружении. Первый эксперимент включает в себя пять этапов монотонных и циклических нагружений с возрастающей монотонной деформацией. Эксперимент состоит из следующих этапов:
-
– 1-й этап включает в себя циклическое нагружение при ε ( m 1) =0, Δε (1) = 0, 016 и N (1) = 20 циклов ;
-
– 2-й этап включает в себя монотонное растяжение до ε (2) = 0,05;
-
– 3-й этап включает в себя циклическое нагружение при ε ( m 3) =0,05, Δε (3) =0,012 и N (3) = 200 циклов ;
-
– 4-й этап включает в себя монотонное растяжение до ε (4) = 0,1;
-
– 5-й этап включает в себя циклическое нагружение при ε ( m 5) = 0,1, Δε (5) = 0,012 и N (5) = Nf циклов до разрушения.
Здесь и далее ε ( m i ) – средняя деформация цикла; Δε ( i ) – размах деформаций цикла; ε ( i ) – достигаемая деформация при монотонном нагружении; N ( i ) – число циклов; i – номер этапа.
На рис. 2 приведена экспериментальная диаграмма деформирования стали 12Х18Н10Т для первого эксперимента, включая все пять этапов. На циклических диаграммах первого, третьего и пятого этапов показаны петли для первого и последнего циклов.
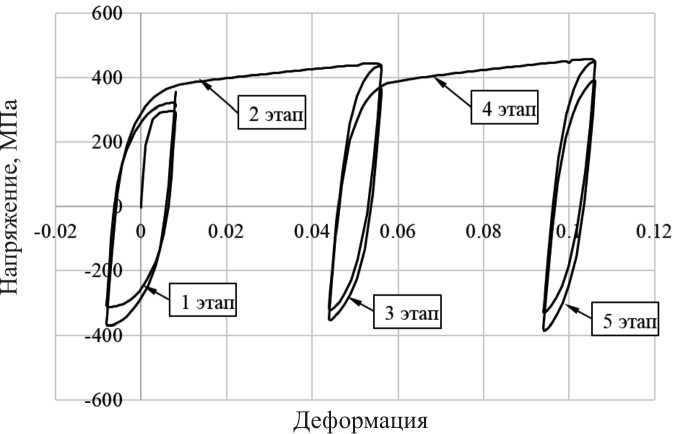
Рис. 2. Диаграмма деформирования стали 12Х18Н10Т для первого эксперимента
Fig. 2. Diagram of deformation of steel 12Kh18N10T for the first experiment
Второй эксперимент включает в себя семь этапов монотонных и циклических нагружений с возрастающей и убывающей монотонной деформацией. Эксперимент состоит из следующих этапов:
-
– 1-й этап включает циклическое нагружение при ε ( m 1) =- 0,006, Δε (1) = 0,012и N (1) = 100циклов ;
-
– 2-й этап – монотонное растяжение до ε (2) = 0,05 ;
-
– 3-й этап – циклическое нагружение при ε ( m 3) = 0,05, Δε (3) = 0,012 и N (3) = 200циклов;
-
– 4-й этап – монотонное сжатие до ε (4) = 0,02 ;
-
– 5-й этап – циклическое нагружение при ε ( m 5) =0,02, Δε (5) =0,012 и N (5) = 200 циклов ;
-
– 6-й этап – монотонное растяжение до ε (6) = 0,05 ;
-
– 7-й этап – циклическое нагружение при ε ( m 7) =0,05, Δε (7) =0,012 и N (7) = Nf циклов до разрушения.
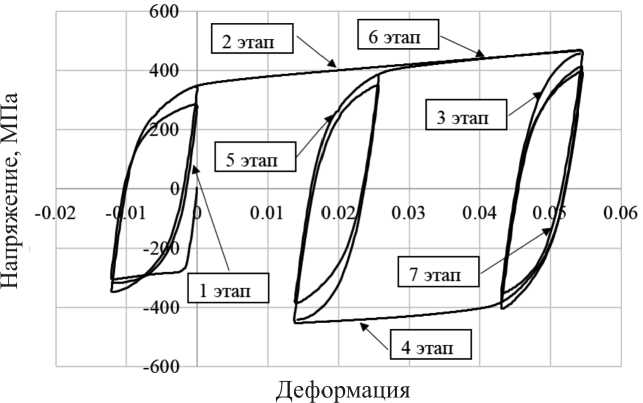
Рис. 3. Диаграмма деформирования стали 12Х18Н10Т для второго эксперимента
Fig. 3. Diagram of deformation of steel 12Kh18N10T for the second experiment
На рис. 3 приведена экспериментальная диаграмма деформирования стали 12Х18Н10Т для второго эксперимента, включая все семь этапов. На циклических диаграммах 1, 3, 5-го и 7-го этапов показаны петли для первого и последнего циклов.
Анализ результатов экспериментальных исследований, представленных на рис. 2, 3, показывает:
– циклическое деформирование на 1-м и последую- щих этапах первого и второго эксперимента является циклически упрочняющимся с последующим замедлением после 1-го этапа процесса циклического упрочнения dC до незначительного ( p ≈ 1МПа), и материал стано-dεp
u вится практически циклически стабильным;
-
– на 3-м и 5-м этапах первого эксперимента и 3, 5-м и 7-м этапах второго эксперимента имеет место посадка петли гистерезиса. Причем процессы посадки на этих этапах идентичны – как будто и не было предварительной истории деформирования;
-
– на 2-м и 4-м этапах первого эксперимента и 2, 4-м и 6-м этапах второго эксперимента монотонное нагру-
- жение осуществляется с одинаковым упрочнением;
– процессы циклического и монотонного нагружений различны, как и процессы анизотропного и изотропного упрочнения при монотонных и циклических нагружениях. К тому же имеют место области перехода от циклического к монотонному и от монотонного к циклическому процессам нагружения.
Для разделения процессов монотонного и циклического деформирования в пространстве тензора пластических деформаций можно ввести поверхность памяти, ограничивающую область циклического деформирования. Из анализа результатов первого эксперимента, представленных на рис. 2, следует, что правая граница поверхности перемещается вправо вместе с правыми границами этапов 1, 3-го и 5-го циклических нагружений. При выходе за поверхность памяти происходит монотонное нагружение – этапы 2 и 4. Из анализа результатов второго эксперимента, представленных на рис. 3, следу- ет, что левая граница поверхности памяти перемещается вместе с левыми границами этапов 1, 3, 5-го и 7-го циклических нагружений. При выходе за поверхность памяти происходит монотонное нагружение – этапы 2, 4 и 6. Этап 4 монотонного нагружения подтверждает, что левая граница поверхности памяти перемещается вместе с левой границей циклического нагружения на этапе 3.
Таким образом поверхность памяти имеет размер, который определяется размахом деформаций при циклическом нагружении, а положение центра определяется значениями средних деформаций при циклическом нагружении.
На рис. 4, 5 приводится кинетика поверхности памяти для первого и второго экспериментов в плоскости компонент Э 1 p иЭ 2 p вектора пластической деформации. Построение поверхности памяти осуществлено в соответствии с результатами экспериментальных исследований, изложенных выше. На первом эксперименте 0-й этап соответствует отнулевому полуциклу. Этапам монотонных нагружений поверхности памяти на рис. 4 и 5 соответствуют концы этапов монотонных нагружений.
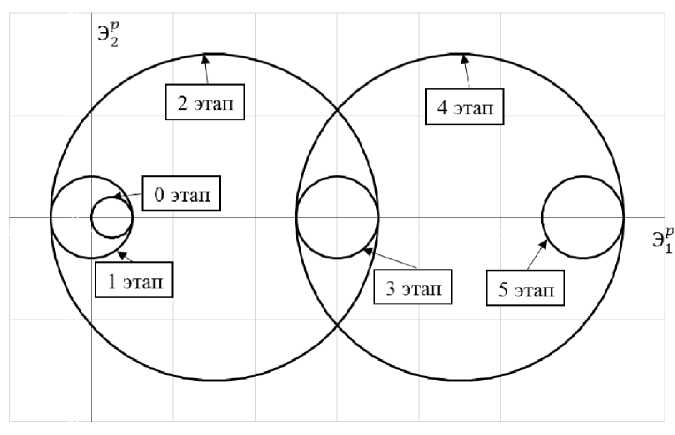
Рис. 4. Кинетика поверхности памяти в первом эксперименте
Fig. 4. Memory surface kinetics in the first experiment
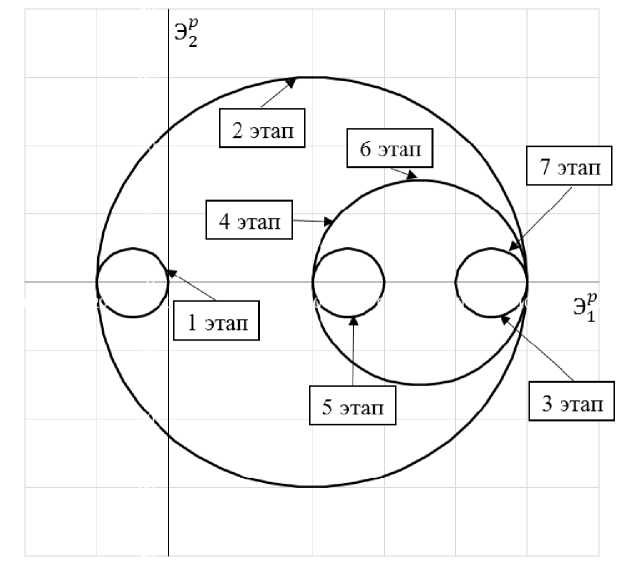
Рис. 5. Кинетика поверхности памяти во втором эксперименте
Fig. 5. Memory surface kinetics in the second experiment
3. Варианты поверхности памяти
Далее рассматриваются и анализируются различные варианты поверхности памяти на основе приведенных выше результатов экспериментальных исследований.
В работах [1–8] для разделения процессов монотонного и циклического деформирования вводится поверхность памяти в пространстве девиатора микронапряжений p iy с определением в процессе деформирования максимального значения интенсивности микронапряжений p max
F p =Pу P j -P max = 0. (1)
Эволюционные уравнения для р у и p max в этих работах задаются в следующем виде:
ру= g 1 s Р - g 2Pyi, (2)
. ( р i p ) H ( F p ) .
P max = 1/-- g 2 P max X ’
( P y P ^ Г
где s ip - тензор скоростей пластической деформации;
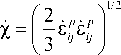
скорость накопленной пластической деформации; g1и g2– модули кинематического уп- рочнения.
H ( F p ) =
1, при F p = 0и P 9 P Ц^ 0, О, при F p < 0и p у Р у < 0.
При одноосном монотонном растяжении, подставляя (2) в (3), можно получить эволюционные уравнения для P max и P
P max = g 1 S p - g 2( P + P max )S p ’ (5)
p = g 1 S p - g 2 PS p ■ (6)
Из уравнений (5) и (6) следует, что определяемые по уравнению (5) максимальные микронапряжения не соответствуют действительным микронапряжениям, определяемым уравнением (6). К тому же при циклическом деформировании при снятии микронапряжений ( p y p y < 0 )
эволюционное уравнение для P max примет вид
P max
g 2 p max X ’
из которого следует, что p max уменьшается до нуля и поверхность памяти стягивается в точку. После чего при увеличении на цикле микронапряжений этот процесс будет определяться как монотонный, что не соответствует действительности.
Следующие варианты поверхности памяти вводятся в пространстве тензора пластических деформаций.
В работах [1; 2; 6] центр поверхности памяти остается в начале системы координат (sip = 0 ), а размер по- верхности определяется как интенсивность максимальной амплитуды пластической деформации.
F Р
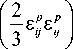
s Р u max
= 0.
Такая поверхность памяти противоречит полученному выше экспериментальному результату о смещении центра поверхности памяти.
Поверхность памяти, центр которой может смещаться, а размер увеличиваться, рассматривается в работах [9–11].
|
F = |
Г 2 z a z Л 3 (е у - ^ у )(е у - ^ у ) |
12 - q s = 0’ |
(9) |
|
<1 s =п H ( F )( И у П * |
Р ’ |
(10) |
|
|
■ ^ , |
= ( 1 -п )^2 H ( F ) nnnn *.j¥ ‘Р ’ |
(11) |
|
, = /1 s p n* = /2 e p ^
‘у V 3 <7 $ iij V 3 q
здесь п - параметр ( п е [ 0,1 ] ) ;
' • D • D pp
Р I 3 ij U )
– скорость
накопленной пластической деформации; H ( x ) - функция Хевисайда.
Как следует из уравнения (10), размер поверхности памяти только увеличивается, тогда как в эксперименте размер поверхности памяти определяется размахом пластических деформаций при циклическом нагружении, и уменьшается при уменьшении размаха пластических деформаций на цикле.
В работе [8] также вводится поверхность памяти, которая может менять свой размер и перемещаться в пространстве тензора пластических деформаций.
F = ( s Р Ч у )( s Р Ч у ) - a max = 0, (13)
где a max – максимальное значение интенсивности тензора пластических деформаций; ^ у - тензор односторонне накопленных пластических деформаций.
В данном подходе размер поверхности памяти только увеличивается, что не соответствует экспериментальным результатам, а при одноосном растяжении этот процесс сразу попадает внутрь поверхности памяти и перестает быть монотонным. К тому же неясно, что происходит с односторонне накопленной пластической деформацией, если она положительна, а затем отрицательна или наоборот.
В работах [12–17] авторов этой статьи для разделения процессов монотонного и циклического деформирования в пространстве пластических деформаций вводится поверхность памяти, которая следует за циклическим нагружением,
F =
2/ 12
3 (s ij - ^ ij )( s ij -^ ij ) - C= ~ 0-
Для вычисления центра и размера поверхности вводятся два тензора пластической деформации s p (1) и £ p (2), определяющие границы поверхности. В начале деформирования эти переменные равны нулю. Определение смещения и размера поверхности памяти происходит в момент смены направления пластического деформирования. В качестве критерия смены направления деформирования принимается следующее условие:
£ p ( t - 0) £ p ( t ) < 0, (15)
где £ p ( t ) - тензор скоростей пластической деформации в текущий момент времени; £ p ( t - 0) - тензор скоростей пластической деформации в предшествующий момент времени.
Условие (15) можно заменить следующим:
s jt - 0) s jt ) < 0, (16)
так как в теории пластического течения при комбинированном упрочнении £ p = X s ij . Здесь s j t ) - девиатор активных [18] напряжений в текущий момент времени; s *( t _ 0)- девиатор активных напряжений в предшествующий момент времени.
В этот момент изменение границ центра и размера поверхности памяти определяется на основе следующих соотношений:
4. Математическое моделирование процессов монотонных и циклических нагружений
Расчетные исследования [12–17] на основе варианта теории пластичности с поверхностью памяти, рассмотренной выше, при моделировании первого эксперимента показывают работоспособность предложенной модели пластичности.
Далее рассматривается моделирование на основе этого варианта [12–17] теории пластичности второго эксперимента, имеющего существенное отличие от первого эксперимента наличием этапа 4 (рис. 3) обратного монотонного деформирования после циклического.
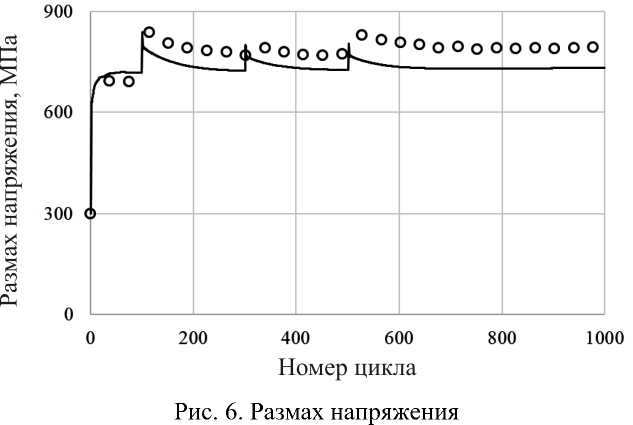
Сравнение расчетных и экспериментальных результатов проводится по изменениям размаха и среднего напряжения на циклах нагружения. На рис. 6, 7 экспериментальные результаты показаны светлыми кружками, а расчетные – сплошными кривыми. Процесс посадки петли пластического гистерезиса иллюстрируется на рис. 7. Циклические диаграммы и этапы монотонного нагружения показаны на рис. 8–11. Здесь также кружки – эксперимент, а сплошные кривые – расчет.
Наблюдается надежное соответствие расчетных и экспериментальных результатов по всему процессу монотонных и циклических нагружений, имеющих место во втором эксперименте. На 7-м этапе циклического нагружения образец был доведен до разрушения. При эксперименте получено 2330 циклов до разрушения, а при расчете – 2400.
Cs =
p (1) p (2) p (2) p
£ ij £ ij , £ ij £ ij ,
= ij
p (1)
£ ij
p (2)
+ £ ij
< pP (2) _ „p (1) 2< „ p (2)
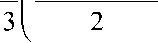
Тогда процесс деформирования будет монотонным или циклическим при выполнении следующих условий:
монотонный при:
F£= 0 U jt-0) Sj(t) ^ 0 ) ,( циклический при: (*
F£= 0 и sy(t-0)sj(t) < 0)-
Данное построение поверхности памяти отвечает всем требованиям, следующим из результатов экспериментальных исследований, приведенных выше.
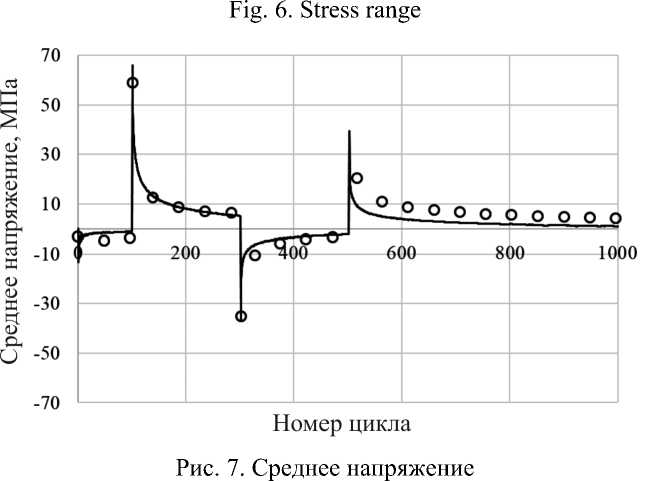
Fig. 7. Medium stress
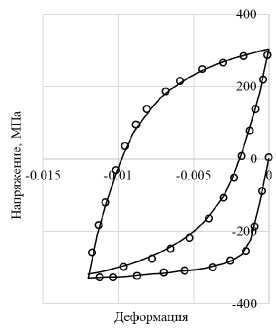
Рис. 8. Первый цикл 1-го этапа нагружения
Fig. 8. The first cycle of the first stage of loading
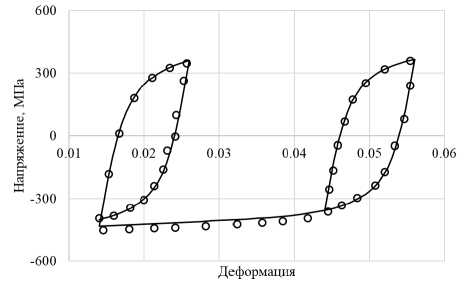
Рис. 10. Последний цикл 3-го этапа, 4-й этап и первый цикл 5-го этапа нагружения
Fig. 10. The last cycle of the third stage, the fourth stage and the first cycle of the fifth loading stage
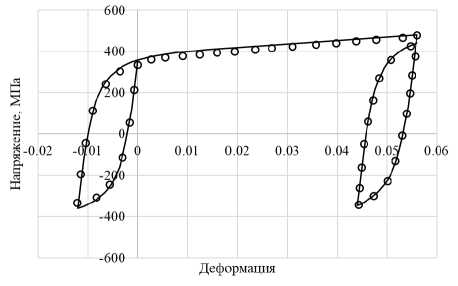
Рис. 9. Последний цикл 1-го этапа, 2-й этап и первый цикл 3-го этапа нагружения
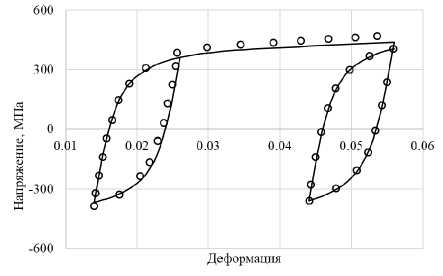
Рис. 11. Последний цикл 5-го этапа, 6-й этап и первый цикл 7-го этапа нагружения
Fig. 9. The last cycle of the first stage, the second stage and the first cycle of the third loading stage
Заключение
На основе анализа результатов экспериментальных исследований нержавеющей стали установлено, что размер поверхности памяти определяется размахами деформаций, а положение центра – значениями средних деформаций при циклическом нагружении. Поверхность памяти разделяет процессы монотонных и циклических нагружений.
Рассмотрены различные варианты поверхности памяти, выявлены их возможности и недостатки и определен наиболее адекватный вариант поверхности памяти.
Список литературы О поверхностях памяти, разделяющих процессы монотонных и циклических нагружений
- Волков И.А., Коротких Ю.Г. Уравнения состояния вязкоупругопластических сред с повреждениями. М.: ФИЗМАТЛИТ, 2008. 424 с.
- Прикладная теория пластичности / Ф.М. Митенков [и др.]. – М.: ФИЗМАТЛИТ, 2015. – 284 с.
- Прикладная теория вязкопластичности: монография / И.А. Волков [и др.]. – Н. Новгород: Изд-во ННГУ, 2015. – 318 с.
- Волков И.А., Игумнов Л.А. Введение в континуальную механику поврежденной среды. – М.: ФИЗМАТЛИТ, 2017. – 304 с.
- Капустин С.А., Чурилов Ю.А., Горохов В.А. Моделирование нелинейного деформирования и разрушения конструкций в условиях многофакторных воздействий на основе МКЭ. – Н. Новгород: Изд-во ННГУ, 2015. – 347 с.
- Коротких Ю.Г. Описание процессов накопления повреждений материала при неизотермическом вязкопластическом деформировании // Проблемы прочности. – 1985. – № 1. – С. 18–23.
- Моделирование усталостной долговечности поликристаллических конструкционных сплавов при блочном несимметричном малоцикловом нагружении / И.А. Волков, Л.А. Игумнов, И.С. Тарасов, Д.Н. Шишулин, М.Т. Маркова // Проблемы прочности и пластичности. – 2018. – Т. 80, № 1. – С.15–30.
- Оценка ресурсных характеристик поликристаллических конструкционных сплавов при циклическом термомеханическом нагружении / И.А. Волков, Л.А. Игумнов, Д.Н. Шишулин, А.А. Белов // Проблемы прочности и пластичности. – 2021. – Т. 83, № 4. – С. 481–504.
- Ohno N. A constitutive model of cyclic plasticity with a nonhardening strain region // J. Appli. Mech. – 1982. – 49. – P. 721–727.
- Chaboche J.L., Dang-Van k., and Cordier G., Modelization of the strain-memory-effect on the cyclic hardening of 316 stainless steel // SMIRT-5 – Division L. – Berlin, 1979.
- Wang Yu. Experimental and numerical evaluations of viscoplastic material behavior and multiaxial for austenitic and ferritic materials: dissertation of Dr. Ing. – C., 2014. – 163 p.
- Бондарь В.С., Абашев Д.Р. Некоторые особенности процессов монотонных и циклических нагружений. Эксперимент и моделирование // Вестник ПНИПУ. Механика. – 2019. – № 2. – С. 25–34.
- Бондарь В.С., Абашев Д.Р., Фомин Д.Ю. Вариант теории термопластичности для монотонных и циклических процессов неизотермических нагружений // Вестник ПНИПУ. Механика. – 2020. – № 2. – С. 28–36.
- Bondar V.S., Abashev D.R. Refining the thermoplasticity theory for modeling monotonic and cyclic loading processes // Journal of mechanics of materials and structures – 2020. – Vol. 15. – № 2. – P. 225–235.
- Bondar V.S., Abashev D.R. Mathematical modeling of the monotonic and cyclic loading processes // Strength of Materials – 2020. – Von. 52. – № 3. – pp. 366–373.
- Bondar V.S., Abashev D.R. Refining the thermoplasticity theory for modeling of cyclic nonisothermic loading processes // Journal of mechanics of materials and structures – 2021. – Vol.
- – № 4. – P. 501–510.
- Bondar V.S., Abashev D.R. Modified theory of plasticity for monotonic and cyclic deformation processes // Mechanics of Solids – 2021. – Vol. 56. – № 1. – P. 4–12.
- Новожилов В.В., Кадашевич Ю.И. Микронапряжения в конструкционных материалах. Л.: Машиностроение, 1990. 224 с.
- Bondar V.S. Inelasticity. Variants of the theory. New York: Begell House, 2013. 194 p.
- Нелинейная механика материалов / Ж. Бессон [и др]. – СПб.: Изд-во Политехн. ун-та, 2010. – 397 с.
- Bari S., Hassan T. An advancement in cyclic plasticity modeling for multiaxial ratcheting simulation // Int. J. of Plasticity. 2002. Vol. 18. P. 873–894.
- Kan Q., Kang G. Constitutive model for uniaxial transformation ratcheting of super-elastic NiTi shape memory alloy at room temperature. // Int. J. of Plasticity. 2009. Vol. 26 (3). P. 441–465. DOI: 10.1016/j.ijplas.2009.08.005
- Chaboche J.-L. A review of some plasticity and viscoplasticity constitutive theories // Int. J. of Plasticity. 2008. − Vol. 24. P. 1642–1692.
- Rahman S.M., Hassan T., Corona E., Evaluation of cyclic plasticity models in ratcheting simulation of straight pipes under cyclic bending and steady internal pressure // Int. J. of Plasticity. 2008. − Vol. 24. P. 1756–1791.
- Abdel-Karim M. Modified kinematic hardening rules for simulations of ratchetting // Int. J. of Plasticity. 2009. − Vol. 25. P. 1560–1587.
- Abdel-Karim M. An evaluation for several kinematic hardening rules on prediction of multiaxial stress-controlled ratchetting. // Int. J. of Plasticity. 2010. − Vol. 26. P. 711–730.
- Chaboche J.-L., Kanouté P., Azzouz F. Cyclic inelastic constitutive equations and their impact on the fatigue life predictions // Int. J. of Plasticity. 2012. − Vol. 35. P. 44–66.
- Hassan T., Taleb L., Krishna S. Influence of nonproportional loading on ratcheting responses and simulations by two recent cyclic plasticity models // Int. J. Plasticity. 2008. − Vol. 24 − P. 1863–1889.
- Effect of dynamic strain aging on isotropic hardening in low cycle fatigue for carbon manganese steel / Z.Y. Huang, J.L. Chaboche, Q.Y. Wang, D. Wagner, C. Bathias // Materials Science and Engineering. − 2014. A589. − P. 34–40.
- Kang G., Kan Q. Contitutive modeling for uniaxial timedependent ratcheting of SS304 stainless steel // Mech. Mater.. 2007. − Vol. 39. − P. 488–499.
- Taleb L., Cailletaud G. Cyclic accumulation of the inelastic strain in the 304L SS under stress control at room temperature: Ratcheting or creep // Int. J. Plasticity. − 2011. Vol. 27 (12). − P. 1936–1958.
- Taleb L. About the cyclic accumulation of the inelastic strain observed in metals subjected to cyclic stress control // Int. J. Plasticity. 2013. − Vol. 43. − P. 1–19.
- Taleb L., Cailletaud G., Saï K. Experimental and numerical analysis about the cyclic behavior of the 304L and 316L stainless steels at 350 °C // Int. J. Plasticity. 2014. − Vol. 61. − P. 32–48.
- Armstrong P.J., Frederick C.O. A mathematical representation of the multiaxial Bauscinger effect // CEGB Report No. RD/B/N/ 731. 1966.
- Кадашевич Ю.И. О различных тензорно-линейных соотношениях в теории пластичности // Исследования по упругости и пластичности. Л.: Изд-во ЛГУ. − 1967. Вып.6. С. 3945.
- Ишлинский А.Ю. Общая теория пластичности с линейным упрочнением // Укр. матем. журн. 1954. − Т. 6, вып. 3. С. 314324.
- Prager W. The theory of plasticity: A Survey of Recent Achievements // Proc. Inst. Mech. Engrs. 1955. − London, 169.41.
- Ohno N., Wang J.-D. Kinematic hardening rules with critical state of dynamic recovery, part 1: formulations and basic features for ratcheting behavior // International Journal of Plasticity. 1993. − Vol. 9. − P. 375–390.
- Бондарь В.С., Абашев Д.Р., Петров В.К. Сравнительный анализ вариантов пластичности при циклических нагружениях // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2017. – № ». – 23–44.
- Бондарь В.С., Абашев Д.Р., Фомин Д.Ю. Теории пластичности при сложном нагружении по плоским траекториям деформаций // Вестник ПНИПУ. Механика. – 2021. – № 3. – С. 35–47.
- Бондарь В.С., Абашев Д.Р., Фомин Д.Ю. Теории пластичности при сложном нагружении по пространственным траекториям деформаций // Вестник ПНИПУ. Механика. – 2021. – № 4. – С. 41–48.


