О повышении яркости оптического излучения

Одним из фундаментальных и, казалось бы, давно разрешенных вопросов оптики, является вопрос о предельно возможной концентрации излучения. Этот вопрос может быть сформулирован по-разному.

Пусть имеется оптическая система, на которую падает и из которой выходит излучение (рис. 1), причем никакой другой энергии на эту систему не поступает*.

Рис. 1

• 1.    Может ли плотность мощности выходного излучения при совершенствовании оптической системы стать сколь угодно большой?

• 2.    Может ли температура выходного излучения быть больше, чем температура входного излучения?

• 3.    Может ли яркость излучения на выходе превысить яркость излучения на входе?

Обычно на это дается отрицательный ответ (см., например [1"^])« Если вопрос задается в первой или третьей формулировке, то отрицательный ответ на него базируется на использовании закона Лагранжа-Гельмгольца [?]» условии синусов [2] и теореме Штраубеля [3] • Отрицательный ответ на вторую формулировку вопроса дается на основании теоремы Лиувилля о сохранении фазового объема Г^1. Наконец, зачастую невозможность неограниченного повышения плотности мощности и повышения яркости объясняют, ссылаясь на закон Кирхгофа либо просто постулируя невозможность повышения температуры излучения, т.е. принимая в качестве аксиомы эквивалентную формулировку [5].

В настоящей работе показывается, что ответ на вопросы первый, второй и третий положительный, т.е. плотность мощности, температуры и яркость излучения могут возрастать в некотором смысле неограниченно. Будут указаны способы создания устройств, которые могут рассматриваться как промежуточные между обычными и лазерными, а также проанализировано понятие антенны оптического излучения. Будет дана подробная оценка пределов применимости некоторых положений оптики и термодинамики излучения.

Как известно, световое поле может быть охарактеризовано энергией Е, прошедшей через площадку о, мощностью W, плотностью мощности J, яркостью В и спект- ральной яркостью В^. Эти величины находятся между собой в следующих соотношениях: t

Е = /Wdt            W = / Jda

°                                                          (1)

J = / В cos 6dfi В = / В dv, Q                     0 V где t - время; Q - телесный угол; 6 - угол между нормалью к поверхности и направлением излучения; V - частота излучения. Яркость В и спектральная яркость В^ -являются наиболее универсальными характеристиками излучения, по которым могут быть определены плотность мощности, мощность и энергия.

Для некогерентного излучения на каждой частоте v может быть определена его эффективная температура Т, зависящая от спектральной яркости на этой частоте:

з hv

с(ехр ~ - 1>

Как видно из [2], эффективная температура и спектральная яркость В^ связаны между собой однозначной зависимостью и в этом смысле эквивалентны Г Излучение с планковским распределением имеет одну и ту же температуру на всех частотах.

Для излучения с яркостью В и произвольным распределением спектральной яркости В^ вводится понятие радиационной температуры Тг, которая равна температуре планковского излучения, обладающего той же яркостью.

Казалось бы, второе начало термодинамики требует невозрастания температуры излучения (Т2 < Т1), так как в противном случае с помощью оптической системы, не потребляющей никакой дополнительной энергии, может быть произведен представляющийся невозможным нагрев объекта до температуры, превышающей температуру источника излучения. На первый взгляд это противоречит невозможности вечного двигателя второго рода. И действительно, именно из условия равенства температур на входе и выходе оптической системы Клаузиусом [б] впервые получено, безусловно, справедливое и важное в геометрической оптике условие синусов, связывающее размеры х , х предмета и изображения с входным и выходным углами ф ,ф2: 12

х sin ф = х sin ф,.                                                           (3)

• 1   12   ³

Условие неувеличения температуры излучения при его распространении обосновывается с помощью теоремы Лиувилля о сохранении фазового объема [4]. Однако эта теорема применима лишь в том случае, когда может быть точно определена траектория каждого луча. Для геометрической оптики последнее выполняется, поэтому температура излучения, а значит, и его яркость, не возрастают.

Условие синусов (3), разумеется, может быть получено и на основе чисто геометрического рассмотрения без привлечения понятия температуры и теоремы Лиувилля. В соответствии с более общей, чем условие синусов, теоремой Штраубеля (вывод см. в [з]), величина n? d О1 dfii                                                                                (4)

является инвариантом.

(Здесь п - показатель преломления). Учитывая определение яркости (1), из теоремы Штраубеля следует, что при одном и том же показателе преломления на входе и выходе оптической системы и отсутствии в ней потерь яркость излучения сохраняется:

В2 = В,.                                                                                (5)

Из определения (1) и равенства (5) следует, что плотность мощности излуче ния на выходе оптической системы равна

J = / В dfl cos 6 = / В бй cos Й,                                                 (6)

• ³    П₂³               п_а¹

где Й2 - телесный угол, в котором сосредоточено выходное излучение. Так как величина Йд не может превышать 4п стерадиан, максимально достижимое значение плотности мощности не может превышать величины

J , = 4лВ,                                                                                (7)

атах 1

Фактически использование фокусирующей оптики (линз, зеркал либо их комбинации) для повышения плотности мощности ставит целью возможно большее увеличение выходного угла йд.

Таким образом, вышеуказанные три формулировки можно считать практически эквивалентными,

Однако в оптике известны процессы, в которых принципиально невозможно определить траекторию луча. Такими процессами являются процессы рассеяния излучения и возможность повышения яркости (температуры) в них требует особого рассмотрения, которое вначале будет проведено на основе общих термодинамических соображений .

Наиболее часто второму началу термодинамики придается формулировка Клаузиу са: невозможен процесс, единственным следствием которого является переход тепла от холодного тела к нагретому [7]. Математическим эквивалентом этого утверждения является требование неуменьшения полной энтропии:

S < S ,                                                                                     (8)

__ вх вых где 5вх и 8вых - исходная и конечная энтропии, учитывающие все процессы. Для оптического некогерентного излучения может быть определена энтропия, излучаемая поверхностью а на всех частотах и по всем направлениям за время t [8]. Величина энтропии определяется распределением спектральной яркости:

S = J da J cos edfl / dt / dv a fi                t ° где h - постоянная Планка, с - скорость света*. Неравенство (8) можно записать в виде

S < S, + S , 1 a д' где S1 и S3 - энтропии падающего и выходящего излучения; S^ - энтропия, возникающая в результате каких-то процессов в оптической системе, например диссипа ции энергии. 8 свою очередь, хотя при отсутствии диссипации все рассеянное излучение обязано обладать большей энтропией, чем падающее, часть выходного излучения может иметь сколь угодно малую энтропию 5д. Другими словами, могут иметь место неравенства

S, < S2 = S2 + S2, но

Энтропия излучения может быть представлена и в виде интеграла по объему [8] . Однако для стационарных процессов, рассматриваемых в данной работе, запись (9) более удобна.

Возможность увеличения температуры излучения может быть проанализирована и с использованием формулировки Клаузиуса для второго начала. В соответствии с ней температура излучения на выходе может быть выше температуры излучения на входе, если произошло необратимое изменение в окружающих телах. Таковым обычно является нагрев "холодильника", в качестве которого в случае излучения может рассматриваться окружающее оптическую систему пространство, свободное от излучения и обладающее поэтому нулевой температурой. Известно, что в геометрической оптике все процессы могут рассматриваться как обратимые и только в этом случае повышение температуры излучения невозможно.

С другой стороны, теорема Штраубеля (^) и эквивалентный ей закон Лагранжа-Гельмгольца, как нетрудно видеть, неприменимы при рассеянии излучения. В частности, при изотропном рассеянии вторичное излучение распространяется с равной вероятностью по всем направлениям, поэтому угол 0д имеет,хотя и максимально возможное, но фиксированное значение, равное 4п стерадиан.

Итак, основные положения термодинамики и оптики, вообще говоря, не запрещают повышения яркости излучения вне пределов применимости геометрической оптики, однако не указывают конкретных условий возможности этого повышения. Одним из таких процессов, как было отмечено в работе [э], является вынужденное излучение с оптической накачкой, в частности лазерное излучение. Существенное превышение яркости лазерного излучения над яркостью накачки объяснялось тем, что определенная часть энергии накачки диссипирует. Это, по мнению автора [9]» имеет кардинальное значение для возможности повышения яркости, обеспечивая необходимый баланс энтропии. Разумеется, нет никаких оснований считать вынужденное излучение единственным оптическим процессом, в котором повышается яркость, а диссипацию энергии - непременным условием ее повышения.

Удобным примером процесса с возможным повышением яркости излучения является люминесценция, которую можно рассматривать как рассеяние с изменением (уменьшением) частоты. В большинстве случаев люминесценция является изотропной. Вследствие этого угол 02, в котором распространяется излучение люминесценции, фиксирован и равен 4п стерадиан, поэтому закон синусов и теорема Штраубеля не выполняются .

Возможность повышения яркости при люминесценции может быть продемонстрирована как точным расчетом, так и с помощью простого качественного рассмотрения.

Точный расчет (рис. 2). Падающее излучение 1 возбуждает излучение люминесценции 2 в люминесцирующем теле произвольной формы 3. Плотность мощности источников излучения люминесценции определяется формой тела, пространственно-угловым распределением падающего излучения, бугеровским показателем поглощения а₁ для этого излучения и составляет величину p(x,y_zz) в каждой точке Cx,y_zz - пространственные координаты). Полная мощность излученной люминесценции Ы^ равна интегралу по объему от p(x_zy_zz):

Ыл = / / /р (xzyzz)dxdydz = / рdv                                            vn/

X у 2                        Vo и равна произведению поглощенной мощности W на энергетический выход люминес ценции nt

Ыл = Z Pdv = ПЫЛ. vo

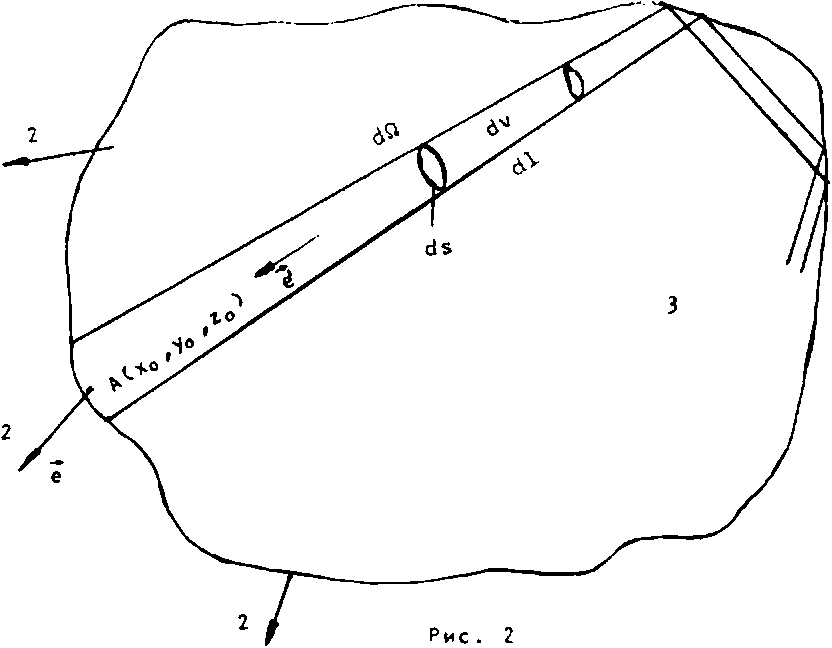
Каждый элемент объема излучает в угол 4п стерадиан, поэтому при изотропной люминесценции в угол dO излучается мощность, равная dW = “ p(x,y,z)dv.                                                       (12)

Выберем произвольную точку А(х0 у0 zQ), лежащую на внутренней поверхности тела 3, и произвольное направление, характеризуемое вектором е\ В этом направлении в точку А(х0 у0 z0) приходит только излучение из области, ограниченной телесным углом dQ. Выделим элемент объема dv , принадлежащий указанному конусу и ограниченный площадкой do. Величина этого объема равна dv = d о dI ,                                                                                 (13)

где dl - элемент длины. Яркость излучения на поверхности этого объема в соответствии с определением (1) и формулой (12) оавна dQ я

4^ Р dv

= р d I 4л

dB = —---- do dfi

Яркость в точке А(х0 у0 zQ), создаваемая вышеуказанным объемом dv, может быть определена на основе инварианта Штраубеля с учетом бугеровского поглощения Qa при прохождении излучением люминесценции расстояния I от элемента объема dv до точки А(х0 у0 z0) :

-a L -a L .

deAz;.= i de = i ’ lodu

Каждый элемент люминесцирующего объема является независимым источником с яркостью, определяемой формулой (1^). Поэтому вклад от всех точек по направлению е* определяется интегрированием по траектории, задаваемой этим направлением. При этом нужно учитывать отражения от поверхности тела 3 и коэффициенты R это-п го отражения :

В*         1 L "а21

А,?' = 4п ' 1 Pdl ♦

I _      .

1 в г                          х                                                              (15)

+ л— R / I p(xzyzz)dl + ...

Li

,                      ^n + l *-

... + 4^ R1 e,,Rn ^     1 p(xzyzz)dl ♦ ...

n

Здесь I - прямолинейные отрезки траектории луча между отражениями. В соответствии с теоремой Штраубеля [3] яркость излучения, выходящего из люминесцирующего объема в точке A(xzyzz) и в направлении е, связанном с направлением е' законом Снеллиуса, равна

В. * А,е

1-R    .

П2 Вл'е'

С1 5а)

где п - показатель преломления.

Довольно громоздкие формулы (15~15а) позволяют точно определить яркость в любой точке и в любом направлении. Рассмотрим некоторые частные случаи, иллюстрирующие возможность повышения яркости и дающие ее расчет.

А. Длинный люминесцирующий световод с квадратным сечением а* а и длиной L, обладающий сильным поглощением на длине волны возбуждающего излучения ^ » а^-1) и слабым поглощением на длине волны люминесценции (а^ « L ¹). Для простоты бу-что все падающее на световод излучение с интенсивностью J₁ логло-равномерно. При этом в соответствии с (11-11а)

дем считать, щается в нем

J a L _ _    1

J ” = т’п-

Согласно (15—15а) яркость излучения, распространяющегося по оси световода, равна на его выходе

В = -^ п.                                                               (16)

4па 1

Если яркость возбуждающего излучения равна

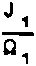
то, учитывая (16), получим условие превышения яркости выходящего излучения над яркостью входного

L J                     J 1

В2 =

Й71 ^ > В1 = "о" *

Откуда

Lo >

4п а 5л

Таким образом, яркость выходного излучения превышает яркость падающего, если длина световода больше, чем L_q.

Б. Световод большой длина (а^Ь » 1) для излучения, распространяющегося в приосевой области (15). Такой световод приобретает максимально возможное значение. Предполагая, как и выше,

J at J получим, проведя интегрирование, значение яркости выходящего'излучения:

В = 7-- а         а_а

(считается, что а -а^ ). Яркость выходящего излучения превышает яркость падающего при выполнении условия

v - п > ^ .                                                            <18>

Последнее выражение имеет важное значение. Параметр v определяется только параметрами материала люминофора: поглощением на длинах волн возбуждающего излучения и люминесценции а-| и аа, энергетическим выходом люминесценции и- Поэтому параметр v также можно считать характеристикой материала. Правая часть (18) является отношением полного телесного угла к углу прихода излучения и не может быть меньше единицы.

Таким образом, параметр v характеризует возможность использования люминес-цирующего материала для повышения яркости и должен превышать для этого единицу. Материалы, удовлетворяющие этому требованию, хорошо известны. Ими, например, являются кристаллы и стекла, активированные ионами редких земель, для которых v может достигать 10а-103, а также некоторые органические красители [10].

Качественное рассмотрение. Вывод о возможности повышения яркости в оптических процессах может быть получен и на основе простых качественных соображений. Рассмотрим длинный световод из люминесцирующего материала (рис. 3^- Пусть яркость падающего на световод излучения равна

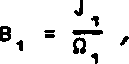
где J - интенсивность этого излучения; 01 - соответствующий телесный угол.

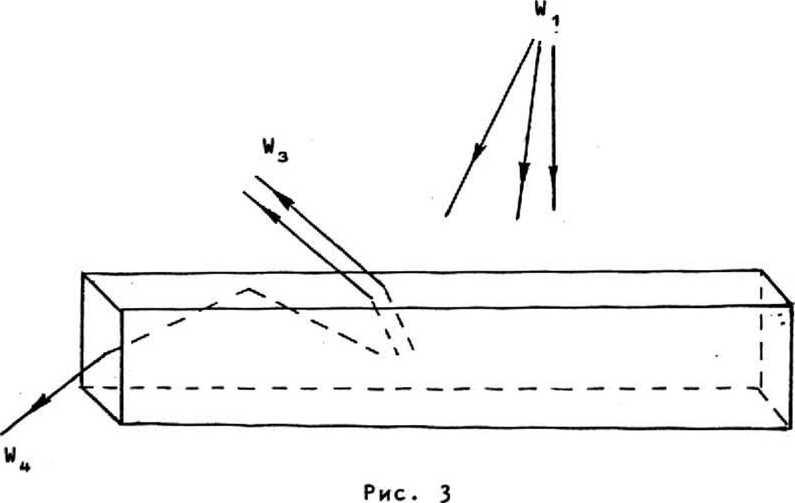
Бугеровский показатель поглощения а2 на длине волны люминесценции будем считать малым, а показатель поглощения возбуждающего излучения достаточно большим. Полная мощность излучения люминесценции W2 пропорциональна мощности W1 падающего излучения и составляет величину

W2 = w3 + WQ = nW^ (Считается, что возбуждающее излучение поглощается полностью).

Основная часть излучения люминесценции Мз выходит через боковую поверхность световода. Меньшая часть излучения люминесценции, распространяясь волноводно, выходит через его торцевую поверхность. Поглощение а2 пренебрежимо мало, поэтому мощность w^ неограниченно растет с увеличением длины световода. Средняя яркость выходящего через торец излучения равна где о2 - площадь торцевой грани; 02 - телесный угол. Так как о2 и 02 постоянны, a W# неограниченно возрастает с увеличением длины, яркость В^ с₽ неограниченно увеличивается и может превысить фиксированное значение яркости падающего излучения (19).

Хотя возможность повышения яркости излучения следует как из точного расчета, так и из простых качественных соображений, ситуацию необходимо проанализи ровать с учетом требований второго начала. В работе [9] показано, что наличие достаточно малого, но вполне определенного поглощения может приводить к удовлетворению требования о возрастании полной энтропии в оптическом процессе. Поэтому рассмотрим случай исчезающе малой диссипации; при этом можно положить, что частоты возбуждающего излучения и излучения люминесценции имеют одно и то же значение V, а выход люминесценции равен единице.

В пренебрежении диссипацией, т.е. энергообменом, исходная и конечная энтропия определяются только входящим и выходящим излучением. Если угол. £)1 , в котором сосредоточено возбуждающее излучение, не слишком велик, то яркость излучения люминесценции, выходящего через боковую поверхность (см. рис. 3) , много яркости выходного излучения, т.е.

меньше

В

N ’ где N » 1. Из определения (1) следует формула, выражающая мощность излучения W через его яркость

W = / da / cos 6dfi / В dv .                                                      (21)

a Q          ° v

Нетрудно видеть, что интегралы (21) и (9), выражающие полную мощность и полную энтропию через яркость, берутся по одним и тем же переменным в одних и тех же пределах. Поэтому если полная мощность сохраняется, а яркость уменьшается в N раз, то в силу аддитивности энтропии идущих в разных направлениях пучков отношение выходной энтропии к входной есть

Г     с2В          с^В      с2В1     с2В1

N (1 + ----7>1п(1 + -----)--- In ----£ f

S _ I ______ Nhv _________ Nhv ______ Nhv ______ Nhv                               (22)

^Si "  _c»b          c²B c²B c²B

(1 + —L)ln(1 * —”>--— In —7- hv           hv hv hv

Это отношение превышает единицу при выполнении эквивалентного условия

Б             1 + В справедливого для любых N > 1 и В > 0, из чего следует, что отношение (22) больше единицы. Последнее означает, что конечная энтропия превышает начальную и требования второго начала выполняются.

Повышение яркости в процессе рассеяния с изменением частоты излучения может быть проиллюстрировано с помощью приближенной аналогии с термодинамическим процессом, в котором роль рабочего тела выполняет излучение, тепловой машиной является люминесцирующее тело, а окружающее люминофор пространство может рассматриваться как холодильник. Так как пространство принимается свободным от излучения, температуру "холодильника" можно считать нулевой. Повышение температуры выходного излучения над температурой падающего можно считать происходящим за счет передачи части тепла холодильнику, что является необратимым процессом. Существенно то обстоятельство, что температура самого люминофора считается близкой к температуре окружающего пространства, т.е. близкой к нулю.

Если угол П, , в котором сосредоточено возбуждающее излучение, достаточно велик, а энергетический выход люминесценции заметно меньше единицы, температуру люминофора уже нельзя считать малой. Температура его определяется при этом условием баланса энергий тепловых и световых потоков, поступающих на люминофор и излученных им. В предельном случае, когда угол П1 имеет максимальное,рав ное 4п значение (например, люминофор находится внутри излучающей полости), излучение люминофора описывается законом Кирхгофа в его общей формулировке, учитывающей пространственное и спектральное распределение излучения Г^1.

Остановимся на возможности применения повышения яркости излучения в конкретных задачах. К настоящему времени известно единственное устройство, повышающее яркость излучения - лазер с оптической накачкой, работу которого можно интерпретировать как преобразование излучения накачки в лазерное излучение, обладающее высокой температурой (яркостью). Важной особенностью лазера является использование вынужденных переходов, что приводит к принципиально пороговому характеру его работы.

Рассмотрим другие возможные устройства, осуществляющие повышение яркости излучения и основанные на использовании люминесценции. В отличие от лазеров они не являются пороговыми и могут быть рассмотрены как промежуточные между обычными и лазерными.

Рассмотренные выше конкретные условия повышения яркости в основном касались протяженных оптических систем и относились к повышению яркости излучения. В принципе,оптическими методами может быть осуществлено и повышение яркости оптического изображения. Рассмотрим в качестве примера систему, изображенную на рис. А. Люминесцирующий оптический элемент 1 в этом случае имеет форму диска. Вышедшее через боковую поверхность оптического элемента излучение люминесценции собирается с помощью обычных световодов 2. При выполнении условия (17), где под Lo необходимо понимать диаметр оптического элемента 1, яркость излучения, выходящего из световода 2, превышает яркость падающего на оптический элемент 1 излучения. Если вся поверхность, на которую падает излучение с каким-то пространственным распределением интенсивности, покрыта оптическими элементами ука- занного типа, то на выходе из световодов это распределение воспроизводится с увеличенной яркостью. Естественно, размер оптического элемента должен быть меньше размера деталей изображения.

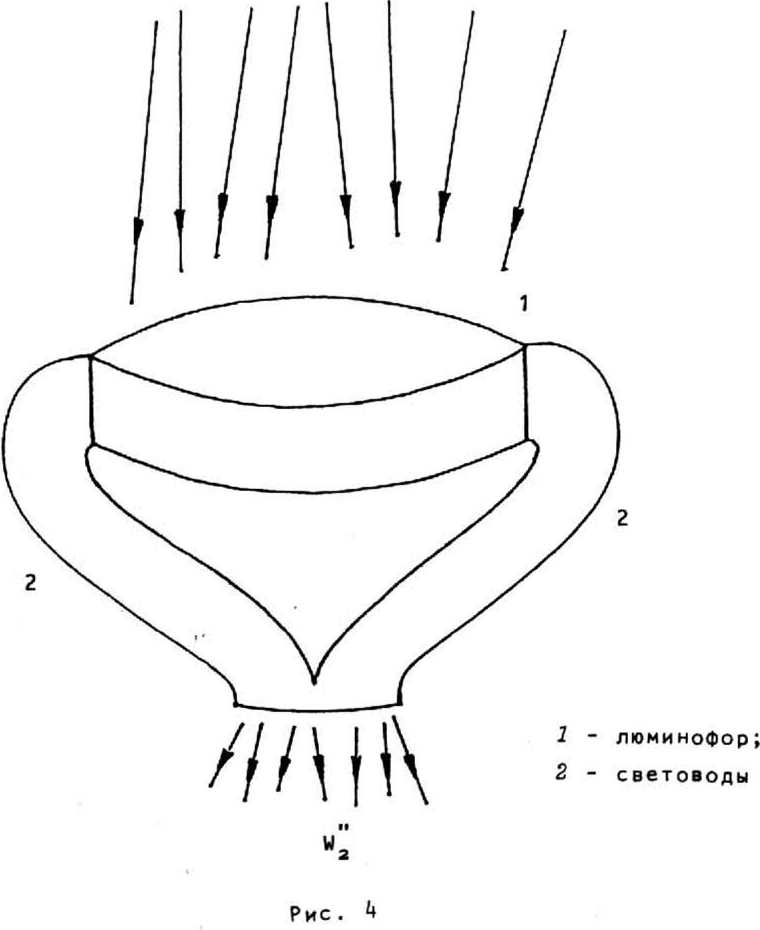
Предельно возможное повышение яркости изображения может быть оценено из соотношения (18). Наиболее оптимальным является увеличение параметра а , так как при этом уменьшается величина Lo, определяющая размер разрешаемых деталей изображения. Этому требованию удовлетворяют ряд полупроводниковых материалов типа All BVI, например CdS, легированный медью и серебром. Для них величина а1 составляет 10^-10® см-1 при возбуждении в область фундаментального поглощения, аа порядка 0,5*1 см 1 для излучения люминесценции с длиной волны 550 нм, а энергетический выход люминесценции и порядка 10-15% [11]. Расчет, проведенный по формуле (15), показывает, что при а1 = 2*10ч см-1, л = 15%, а2 = 1 см-1, П = = 0,05 яркость изображения увеличивается в пять раз при использовании оптического элемента диаметром 0,5 мм.

Возможным вариантом применения повышения яркости излучения при люминесценции является использование этого явления для обнаружения излучения. На рис. 5 приведена схема приемника излучения с люминесцентным спектрально-пространственным преобразователем 1, имеющим клиновидную форму и установленным непосредственно перед входным окном фотоприемника 2. Детектируемое излучение 3, поглощаяо в слое толщиной порядка а”¹, преобразуется в излучение люминесценции 4. Это излучение, отражаясь от боковых поверхностей преобразователя 1, распространяет-

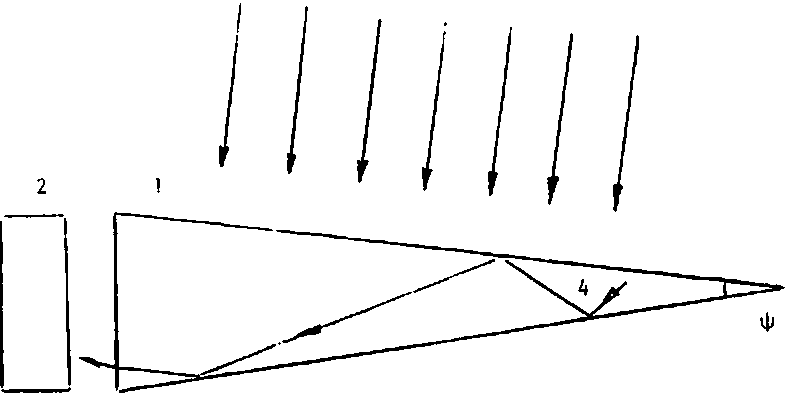
Рис. 5

ся по направлению к фотоприемнику 2. Процесс распространения излучения люминесценции аналогичен распространению излучения в обычном оптическом волноводе с тем важным отличием, что при каждом отражении от поверхности преобразователя направление излучения смещается на угол ф относительно первоначального направления (ф - угол при вершине клина). В результате этого на выходе преобразователя излучение люминесценции сконцентрировано в основном в небольшом угле порядка ф и потери на френелевское отражение становятся пренебрежимо малыми.

Значительное (на 1-2 порядка) увеличение интенсивности излучения достигается за счет того, что в результате люминесцентного преобразования концентрируется излучение со всей поверхности преобразователя, площадь поверхности которого многократно превышает площадь рабочей поверхности фотоприемника.

Важным достоинством изображенного на рис. 5 устройства является большой угол обзора, составляющий 4п стерадиан.

На рис. 6 приведено схематическое изображение устройства обнаружения излучения, отличающегося от предыдущего тем, что люминесцентный преобразователь -концентратор 1 помещен в фокусе отражателя - цилиндрического или параболического зеркала 2. Такое расположение многократно увеличивает величину сигнала, регистрируемого фотоприемником 3, и во столько же раз уменьшает угол приема излучения. Это обстоятельство, при условии поворота отражателя в направлении, показанном на рис. 6 стрелкой, дает возможность определения одного из координатных углов прихода излучения. Очевидно, что два таких устройства с преобразователями, расположенными взаимно перпендикулярно, позволяют полностью определить угловые координаты источника излучения.

В связи с вопросами, обсуждаемыми в данной работе, рассмотрим в заключение понятие антенны оптического излучения. В радиофизике, как известно, антенной называют устройство, позволяющее эффективно преобразовывать падающее излучение и передавать его к приемнику [12]. Традиционно оптические зеркала и линзы к антеннам не относятся. Как отмечалось выше, эти элементы и любые их комбинации не повышают яркость излучения, которая эквивалентна плотности фотонов на моду [13].

Основным свойством антенны является осуществление преобразования поля одного типа (моды, пришедшей из пространства) в моду, бегущую по линии передачи [12]. При этом может повышаться яркость, т.е. количество фотонов на моду [ 1 3} - В отличие от известных оптических устройств описанные выше устройства обладают этим свойством. В частности, устройства, схематически изображенные на рис. 5 и 6, можно рассматривать как волноводы с объемным возбуждением, причем в первом из них осуществлено согласование с приемником.

• 1    - преобразователь;

• 2    - отражатель;

• 3    - фотоприемник

  
  
  

  Рис. 6

  
  

  -Необходимо отметить важное отличие антенны оптического излучения от антенны радиодиапазона. Частоты излучения в радиодиапазоне существенно ниже, чем характерные частоты электронов в металле, поэтому распространяющийся по антенне сигнал совпадает по частоте (и обычно когерентен) с падающим. В устройствах типа описанных выше частота и фаза рассеянного излучения не совпадают с частотой и фазой падающего излучения, поэтому рассеяние является некогерентным и антенна необратима даже в термодинамически нестрогом смысле, т.е. не может использоваться как излучатель. Частотный диапазон приема такой антенны определяется спектрами поглощения и возбуждения люминесценции и может быть как очень широким (от рентгеновского до ИК диапазона), так и весьма узким при использовании фильтрации.                                                                               ¹

• 5.    Гвозде 60 Н.П. , Корки на ..И. Теория оптических систем и оптические измерения. ^м-^: Машиностроение, 1981.

• 6.    Планк У. Введение в теоретическую физику. М.-Л., 1935.

• 7.    Clauai us л. Annalen der Phvsik und- Chemie, v. 121, p. 1-44 (1 864).

• 8.    Планк M. Теория теплового излучения. M., 1935.

• 9-    ПоОслъаа н И.И. УФН , т. 113, в. А, с. 701 (197М.

• 10.    Справочник по лазерам /Под ред. акад. А.М. Прохорова. М.: Сов. радио , 1 978 .

• 11.    Физика и химия соединений All BIV /Под ред. С.А. Медведева. М . : Мир, 1 9 70 .

• 12.    Физическая Энциклопедия. T. 1. M.: Сов. энциклопедия, 1988.

• 13.    Клишко Д.Н. Фотоны и нелинейная оптика. М.: Наука, 1980.