О применении метода Фурье-мод к расчёту локализованных мод интегральных оптических резонаторов

В последнее время большое внимание уделяется изучению оптических свойств резонансных дифракционных структур [1-6]. Простейшим примером периодической резонансной дифракционной структуры является субволновая дифракционная решётка (рис. 1 а ).

а)

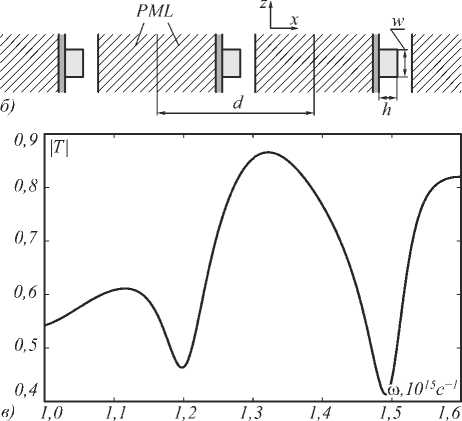
Рис. 1. Геометрия периодической структуры: система ступенек на металлическом слое (структура бесконечна в направлении оси у) (а); геометрия непериодической структуры: двумерный прямоугольный резонатор на толстом металлическом слое (структура бесконечна в направлении оси у) (б); спектр прохождения поверхностного плазмон-поляритона через прямоугольный резонатор (длина w = 900 нм, высота h = 600 нм, диэлектрическая проницаемость е = 5,5 ) на слое серебра толщиной 200 нм (в)

В таких структурах наблюдаются резонансы в виде резких максимумов и минимумов в спектрах отражения и пропускания. Резонансы дифракционных структур обусловлены возбуждением собственных мод структуры [1, 5, 6]. Такие моды описываются комплексным значением частоты [1, 2, 6]. Модами периодической структуры могут быть квазиволноводные моды, распространяющиеся в направлении периодич- ности структуры [1], или локализованные моды (щелей или ступенек) структуры [4]. Одним из наиболее универсальных методов расчёта дифракции света на периодических структурах является метод фурье-мод (в англ. литературе – Rigorous Coupled-Wave Analysis или Fourier Modal Method) [7]. Для расчёта собственных мод периодических дифракционных структур разработана модификация данного метода, основанная на вычислении полюсов аналитического продолжения матрицы рассеяния структуры [1, 6].

С практической точки зрения больший интерес представляет исследование резонансов в непериодических дифракционных структурах. Для расчёта дифракции света на непериодических структурах разработан апериодический вариант метода фурье-мод (в англ. литературе – Aperiodic Fourier Modal Method) [8, 9]. Данный метод основан на рассмотрении периодической структуры, соседние периоды которой оптически изолированы. Изоляция достигается либо применением анизотропных (PML) или градиентных поглощающих слоёв [8], либо введением комплексного преобразования координат [9].

При решении задачи дифракции света на непериодической структуре наблюдаются резонансы, аналогичные резонансам дифракционных решёток, за тем лишь исключением, что они обусловлены возбуждением исключительно локализованных мод. Расчёт локализованных мод непериодических структур – важная задача при проектировании и исследовании элементов интегральной и плазмонной оптики, таких как резонаторы вертикально-излучающих лазеров (VCSEL) и спазеров, элементы для ввода и вывода излучения из волновода. В известных работах предложено несколько методов расчёта локализованных мод [3, 10–12]. Наиболее распространённым является метод, заключающийся в анализе временной зависимости амплитуды электромагнитного поля в рамках FDTD-подхода [10]. Недостатком данного метода является низкая точность расчёта низкодобротных мод и невозможность расчёта распределения поля отдельно взятой моды. В работе [11] рассчитываются моды лазерных резонаторов: для этого используется апериодический метод фурье-мод. Данный метод позво- ляет рассчитывать только лазерные моды с действительной частотой. В работе [12] разработана модификация метода фурье-мод в цилиндрической системе координат, которая позволяет рассчитывать моды радиально-симметричных резонаторов.

В настоящей работе предлагается строгий метод расчёта мод непериодических дифракционных структур, основанный на вычислении полюсов аналитического продолжения матрицы рассеяния. Предложенный метод, основанный на апериодическом методе фурье-мод, позволяет рассчитывать комплексные частоты мод и распределение их поля. Несмотря на схожесть периодического и апериодического методов фурье-мод, задача расчёта мод непериодических структур существенно сложнее и включает ряд особенностей, требующих отдельного рассмотрения.

S —1 ^ scatt = 0

То есть при частоте to p существует нетривиальное решение уравнений Максвелла, не содержащее падающих волн, а это значит, что частоте to p соответствует мода структуры [6]. Зафиксируем теперь падающую плоскую волну и рассмотрим отдельный элемент матрицы рассеяния, соответствующий комплексному коэффициенту пропускания (или отражения) структуры. Если мода, соответствующая полюсу матрицы рассеяния to p , возбуждается падающей волной, то to p также будет являться полюсом коэффициента пропускания (отражения) T ( to ). Тогда для T ( to ) справедливо следующее приближённое соотношение, имеющее смысл отрезка ряда Лорана в окрестности точки to p [14]:

T (to) — a + bj (to-top). (3)

1. Моды и резонансы периодических дифракционных структур

Рассмотрим сначала задачу дифракции электромагнитной волны на периодической структуре (дифракционной решётке) (см. рис. 1 а ). Будем считать, что электромагнитные волны падают на структуру сверху и снизу. Обычно рассматривается падение плоских волн, однако в общем случае можно рассмотреть падение электромагнитных волн, распределение полей которых квазипериодично с тем же периодом, что и у рассматриваемой структуры. Как следует из теоремы Блоха– Флоке, прошедшее и отражённое поле в этом случае можно представить в виде разложения Рэлея, то есть в виде разложения по плоским волнам (распространяющимся и затухающим порядкам дифракции). Падающее излучение также можно представить в виде разложения по плоским волнам. Тогда решение задачи дифракции состоит в нахождении амплитуд рассеянных плоских волн (порядков дифракции) по заданным амплитудам падающих плоских волн. Решение задачи дифракции можно представить через матрицу рассеяния [2, 6, 13]. Матрица рассеяния решётки S связывает комплексные амплитуды волн, падающих на решётку ( T inc ), и амплитуды волн, рассеянных решёткой ( T scatt ), в виде:

Ψ ^scatt = S · Ψ ^inc, (1)

Представление коэффициента пропускания (3), справедливое в окрестности частоты собственной моды структуры, объясняет резонансные особенности в спектре пропускания. Таким образом, задача анализа и объяснения резонансов структуры сводится к задаче расчёта комплексных частот собственных мод структуры. Отметим, что действительная часть комплексной частоты задаёт частоту резонанса, а мнимая часть определяет добротность резонанса Q =Re to p /(-2Im to p ).

где Ψ ^inc

I 1

I 2

_Ψ scatt

R

T

R и T – векторы ком-

плексных амплитуд отражённых и прошедших порядков дифракции, а I 1 и I 2 – векторы комплексных амплитуд плоских волн, падающих на структуру сверху и снизу. Элемент матрицы рассеяния с индексом ( I, j ) задаёт амплитуду рассеяния падающей волны с номером j в рассеянную волну с номером i .

Матрица рассеяния имеет физический смысл только при действительных частотах. Рассмотрим аналитическое продолжение матрицы рассеяния на комплексную to- плоскость. Предположим, что определитель матрицы S ( to ) имеет комплексный полюс при to = to p . В этом случае det S ^-1( to p ) = 0 и существуют нетривиальные решения однородного уравнения:

2. Моды и резонансы непериодических дифракционных структур

Рассмотрим теперь непериодическую задачу, соответствующую дифракции моды плоскопараллельного волновода на неоднородности (резонаторе). В этом случае падающее и рассеянное излучение распространяются не в свободном пространстве, а в среде, содержащей плоскопараллельный волновод. В частности, на рис. 1 б над и под структурой находится металлический (плазмонный) волновод. Анализ непериодической дифракционной структуры может быть сведён к анализу периодической структуры следующим образом. Рассматриваемая непериодическая структура периодически продолжается (см. рис. 1 б ), при этом либо соседние периоды отделяются идеально согласованными поглощающими (PML) слоями (штрихованная область на рис. 1 б ) [8], либо вводится комплексное преобразование координат [9]. При этом соседние периоды становятся оптически изолированными и, соответственно, решение задачи дифракции на периодически продолженной структуре совпадает с решением задачи дифракции на непериодической структуре. Таким образом, над и под структурой вместо однородной подложки (рис. 1 а ) оказывается периодическая среда (рис. 1 б ). Аналогом разложения Рэлея для рассеянного и падающего поля в этом случае служит разложение по модам периодической среды.

В качестве примера рассмотрим задачу прохождения плазмонной моды толстой серебряной плёнки через диэлектрическую ступеньку (рис. 1 б ; параметры структуры приведены в подписи к рисунку). Спектр пропускания представлен на рис. 1 в . При этом под коэффициентом пропускания понимается отношение

комплексной амплитуды прошедшей плазмонной моды к комплексной амплитуде падающей моды. В спектре пропускания наблюдаются выраженные резонансные особенности, поэтому актуальной является задача расчёта (комплексных частот) собственных мод непериодической структуры. Расчёт собственных мод позволит объяснить указанные особенности спектра пропускания и найти численные характеристики резонансов.

Для расчёта полюсов матрицы рассеяния (коэффициента пропускания) необходимо уметь вычислять матрицу рассеяния (коэффициент пропускания) при комплексных значениях частоты. Одним из наиболее универсальных методов расчёта матрицы рассеяния является метод фурье-мод [7, 15]. В следующем разделе приведены основные необходимые формулы метода фурье-мод в случае действительной частоты, а затем рассмотрен вопрос построения аналитического продолжения.

3.    Метод фурье-мод

Метод фурье-мод основан на теореме Блоха– Флоке, из которой следует, что решение уравнений Максвелла в периодической структуре можно представить в виде квазипериодической функции. В рамках метода фурье-мод предполагается, что структура состоит из слоёв, в которых диэлектрическая проницаемость материалов не зависит от переменной z . В этом случае поле в каждом слое можно представить в виде ряда Фурье по переменной x , соответствующей направлению периодичности структуры [7, 15] (см. рис. 1 a , б ). Пусть Φ _i ( z ) – вектор, состоящий из фурье-коэффициентов тангенциальных компонент электромагнитного поля в i -м слое ( i =1,…, L ). Вектор Φ i ( z ) имеет размерность 4 N , где N – используемое число фурье-гармоник. Из уравнений Максвелла следует, что Φ i ( z ) удовлетворяет следующему матричному дифференциальному уравнению:

d Φ z

—/■=Ai •Ф i (z),

где матрица A i e C 4 N ^x 4 N определяется геометрией i -го слоя и параметрами падающей на структуру волны (частота, квазиволновое число) [7, 15]. Решением уравнения (4) является представление поля в i -м слое:

^Ф i ( ^z ) = ^ex P ( ^z A i ) ^C i = W i ^ex P ( ^{z Л} i ) ^C i , (5) где W i – матрица, столбцы которой являются собственными векторами матрицы A i ; ± Л i - диагональная матрица соответствующих собственных значений; C i – вектор произвольных постоянных.

Выражение (5) следует рассматривать как разложение поля в i-м слое по модам этого слоя, распространяющимся в направлении оси z. При этом константа распространения j-й моды в направлении оси z определяется на основе собственного числа %j (при использовании зависимости от времени в виде e-i“‘ получаем, что kz,j = -i%j). Поперечное распределение поля этой моды задаётся j-м столбцом матрицы Wi. При этом элементы j-го столбца являются фурье-коэффициентами в разложении поля по переменной x.

Для решения уравнений Максвелла в многослойной структуре необходимо приравнять тангенциальные компоненты (или, что то же, фурье-коэффициенты тангенциальных компонент) электромагнитного поля на границах раздела слоёв. В результате получается следующая система уравнений:

Ф i ( Z i ) = Ф i +i ( z, ) , i = 0,..., L ,                (6)

где z = z_i – граница раздела слоёв с номерами i и i +1. В системе (6) присутствуют величины Ф ₀( z ₀) и Ф _{L +1}( z_L ), имеющие смысл фурье-коэффициентов в разложениях поля над структурой (на верхней её границе) и под структурой (на нижней границе).

Рассмотрим решение задачи дифракции моды на структуре. Пусть на структуру сверху падает мода, распределение поля которой описывается вектором фурье-коэффициентов V inc . Полагается, что V inc – один из столбцов матрицы W ₀. При дифракции моды на структуре образуется набор рассеянных (отражённых и прошедших) мод. Пусть матрицa V _r состоит из тех столбцов матрицы W ₀, которые описывают отражённые моды, а матрица V _t – из тех столбцов матрицы W L =1 , которые описывают прошедшие моды. Тогда поле над структурой мы можем записать как суперпозицию отражённых мод и падающей моды

Ф о ( z о ) = V_r R + V ine ,

V _r e C

4 N x2 N

V ine e C⁴ N ^{x 1},

R e C2 N x1, где R – вектор комплексных амплитуд отражённых мод. Поле под структурой записывается как суперпозиция прошедших мод:

Ф _{L + 1} ( z_L ) = V , T , V , e C⁴ N ^{x 2} N , T e C² N ^{x 1}, (8)

где T – вектор комплексных амплитуд прошедших мод. Отметим, что в настоящей работе не приведён общий вид матриц A , V _r , V _inc , V _t , Ф _i ( z ) из-за их громоздкости. Однако вид данных матриц приведён в работах [7, 15]. В частности, в работе [15] использованы следующие обозначения: V r = P ^{( U )}, V inc = D , V , = P ⁽ D ) , Ф i ( z ) = [ S TT ( z ) S T ( z ) U T ( z ) U T^T ( z ) ] T .

Уравнения (6), (7), (8) представляют собой систему линейных уравнений относительно неизвестных амплитуд отражённых и прошедших мод ( R и T ). В решении данной системы линейных уравнений и состоит решение задачи дифракции. Отметим, что на практике при решении данной системы применяется ряд методов, позволяющих избежать проблем с численной неустойчивостью [7, 13, 16, 15]. Кроме того, при вычислении матрицы A i также есть ряд особенностей [17, 15].

Если над и под структурой находится однородная среда (см. рис. 1а), модами 0-го и L+1-го слоёв являются плоские волны (распространяющиеся и зату- хающие порядки дифракции). В этом случае матрицы Ao, AL+1 имеют простой вид и матрицы Vt, Vr, Vinc выписываются аналитически. При этом разложения (7), (8) называются разложениями Рэлея.

В общем случае матрицы Vt, Vr, Vinc получаются выбором соответствующих столбцов из матрицы W. Под «соответствующими» здесь понимается следующее. Матрица Vt должна содержать столбцы матрицы WL+1, описывающие прошедшие моды, матрица Vr – столбцы матрицы W0, описывающие отражённые моды, вектор Vinc – столбец матрицы W0, описывающий падающую моду. В большинстве случаев (для взаимных материалов) для каждой моды с константой распространения kz находится «парная» мода с константой распространения – kz. При этом одна из этих мод – падающая, а вторая – рассеянная. Таким образом, для решения задачи дифракции требуется разделить все моды (над и под структурой) на падающие и рассеянные. Моды можно разделять по направлению распространения (по знаку действительной части kz) или по направлению затухания (по знаку мнимой час- ти kz). Разделение мод на падающие и рассеянные – достаточно тонкая проблема, которая решается с учётом физического смысла решаемой задачи.

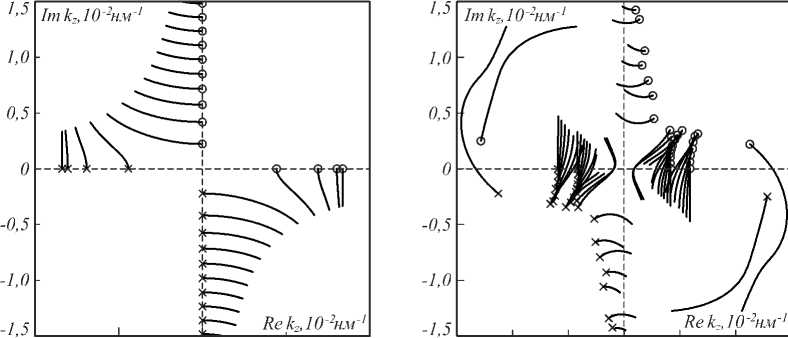
Если над (под) структурой находится однородная непоглощающая среда (рис. 1 а ), то моды (плоские волны) над структурой являются либо распространяющимися, либо затухающими. В этом случае рассеянные моды выбираются из условия, что, будучи распространяющимися, они должны распространяться в направлении «от» структуры, а будучи затухающими, – затухать при удалении от структуры. Например, при использовании зависимости от времени в виде e^{-i m} t отражёнными волнами (в области над структурой) будут распространяющиеся моды (порядки дифракции) c Im k_z =0, Re k_z >0, а также затухающие моды (порядки дифракции) с Re k z =0, Im k z >0. На рис. 2 а крестиками и окружностями показаны значения комплексной константы распространения k_z = ±^ ( ю/ c ) 2 - ( (2л/ d ) • n ) 2 , где d = 5300 нм.

О 0,5    1,0 1,5

Рис. 2. Константы распространения (k_z) мод над структурой: (а) однородная среда (см. рис. 1a) и (б) периодическая среда (см. рис. 1б; показаны не все моды). При действительной частоте to = 1,256x10 15 падающие моды обозначены крестиками, рассеянные – окружностями. Линиями показано изменение констант распространения при добавлении отрицательной мнимой части к частоте в диапазоне от 0 до – 10¹⁵i

Если под структурой находится не однородная, а периодическая среда (бесконечная решётка, рис. 1б), то константы распространения kz, как правило, являются комплексными с ненулевыми действительной и мнимой частями. При этом направление затухания моды (определяемое знаком Imkz) и направление, определяемое по знаку Rekz, могут отличаться. Таким образом, задача определения направления распространения моды требует отдельного рассмотрения. Особенно актуальной эта проблема становится при расчёте локализованных мод плазмонных элементов, когда над (под) структурой одновременно могут присутствовать диэлектрик, металл и анизотропные PML-материалы. В этом случае разделение мод на падающие и рассеянные производится следующим образом: моды с действительным kz по-прежнему можно разделить по направлению их распространения. Остальные же моды (у которых kz комплексно) следует разделить по направлению затухания [8]. Это гарантирует, что поле, полученное как результат решения задачи дифракции, не будет возрастать при удалении от структуры. Таким образом, отражёнными модами будут моды c Imkz = 0, Rekz >0, а также моды с Imkz > 0 (рис. 2б).

Таким образом, выбрав из общего набора мод над (под) структурой отражённые (прошедшие) моды, а также выбрав падающую моду, мы можем решить задачу дифракции. В частности, можно вычислить зависимость коэффициента пропускания моды от действительной частоты ( T ( to )). Как было указано выше, для объяснения резонансов необходимо рассмотреть задачу построения аналитического продолжения функции T ( to ) на комплексную to -плоскость.

4.    Построение аналитического продолжения

Для вычисления коэффициента пропускания при комплексной частоте, как и в вышеизложенном методе фурье-мод, мы должны вычислить собственное разложение матрицы A для областей над (под) структурой и разделить моды (т. е. собственные векторы и соответствующие им собственные числа) на два класса: падающие и рассеянные. Для обеспечения аналитичности T(го) мы должны обеспечить аналитичность элементов матриц Vt, Vr и Vinc, рассматриваемых как функции частоты. Главное отличие от случая действительной частоты состоит в том, что при комплексных частотах мы не можем руководствоваться физическими соображениями при разделении мод на падающие и рассеянные.

На рис. 2 а представлено изменение констант распространения падающих (линии с крестиком) и рассеянных (линии с окружностями) мод над структурой при добавлении к действительной частоте мнимой части (Im ro <0). Из рисунка видно, что рассеянные (отражённые) моды, которые были распространяющими ( k_z е Р ' ), при добавлении мнимой части к частоте становятся экспоненциально возрастающими (приобретают отрицательную мнимую часть). Таким образом, в случае комплексной частоты мы не можем полагаться на направление распространения или затухания мод при построении матриц V _t , V _r и V _inc.

В простейшем случае, когда над (под) периодической структурой находится однородный диэлектрик (рис. 1 а ), представление поля над (под) структурой задаётся аналитически [7]. В этом случае построение аналитического продолжения матриц V t , V r и V inc (а соответственно, и аналитического продолжения T ( го )) является тривиальным [1].

В общем случае, когда над и под структурой находится неоднородная периодическая среда (рис. 1 б ), аналитическое выражение для собственных векторов матрицы A неизвестно и задача построения аналитического продолжения становится существенно сложнее. Единственное условие, исходя из которого следует разделять моды на падающие–рассеянные (т. е. построить вышеуказанные матрицы), можно сформулировать следующим образом. При комплексной частоте мода является падающей (рассеянной) тогда и только тогда, когда при уменьшении мнимой части комплексной частоты до нуля эта мода становится падающей (рассеянной) в смысле определения падающей (рассеянной) моды при действительной частоте.

Таким образом, разделение мод на падающие и рассеянные можно осуществить, разделив моды при действительной частоте, а затем, плавно увеличивая частоту, «проследить» за каждой из мод. На практике достаточно «следить» за изменением констант распространения мод, используя следующий метод.

Сначала следует рассчитать моды среды над (под) структурой в случае действительной частоты Гоо = Rero и разделить эти моды на падаю-щие/рассеянные. Затем следует рассчитать моды при комплексной частоте ro1=Rero+ ilmro. Каждой из мод на частоте ro1 ставится во взаимно-однозначное соответствие «ближайшая» мода на частоте ro0. Мода на частоте ro1 считается падающей (рассеянной), если соответствующая мода на частоте ro0 является падающей (рассеянной).

Предложенный метод позволяет поставить в соответствие каждой моде на частоте ro 1 моду на частоте ro 0 , при этом минимизируется суммарное изменение констант распространения мод. Отметим, что построение взаимно-однозначного соответствия между модами является наиболее времязатратной операцией. Предлагается использовать следующий метод. Формируется матрица «близости» мод, элементы которой определены как

( P )„ = I k - , — ^k J, (9)

где k_z,i – константы распространения мод на частоте ro 0 , k_Zj - набор констант распространения мод на частоте ro 1 . Затем для матрицы P решается задача о назначениях с использованием венгерского алгоритма [18]. Вообще говоря, если мнимая часть частоты рассчитываемой моды достаточно велика, то даже использование предложенного алгоритма может дать неверный результат, так как константы распространения мод на частоте ro 1 могут существенно отличаться от констант распространения мод на частоте ro 0 . В этом случае целесообразно применять предложенный метод K раз, последовательно увеличивая значение мнимой части частоты: ro k = Re ro + i( k / K) Im ro , k = 0… K . «Эволюционные» кривые на рис. 2, показывающие изменения констант распространения, были рассчитаны с использованием данного метода при большом значении K . При расчёте мод использовалось K = 1+[-10^-13Im ro ].

Отметим, что в отдельных случаях разделение мод на падающие–рассеянные может быть осуществлено приближённо [3], например, по знаку величины Re k_z + Im k_z . Однако данный приближённый подход работает не во всех случаях. В частности, такое разделение оказывается неверным при большой мнимой части комплексной частоты (см. рис. 2 б ). Кроме того, приближённое разделение мод приводит к неправильному расчёту поля моды вне резонатора.

В настоящем разделе приведено построение аналитического продолжения коэффициента пропускания T ( ro ). Аналитическое продолжение всей матрицы рассеяния строится аналогично.

5.    Аномалии Рэлея

Выше описан общий метод разделения мод на падающие и рассеянные моды. При этом не рассмотрен один важный случай. Если одна из мод имеет константу распространения k z =0, то в наборе мод должны присутствовать две моды с k z =0. Одну из них следует считать падающей, вторую – рассеянной. Таким образом, мы имеем случай, когда падающую моду не удаётся отличить от рассеянной.

Для дифракционной решётки (рис. 1а) этот особый случай соответствует аномалиям Рэлея. Они наблюдаются на частотах Рэлея одного из порядков дифракции. При частотах, меньших частоты Рэлея, этот порядок дифракции является затухающим (i kz ∈ ℝ ), а при частотах больших частоты Рэлея – распространяющимся (kz ∈ ℝ ). Если говорить в терминах аналитического продолжения функции пропускания, то аномалии Рэлея – точки ветвления функции пропускания. Наличие точек ветвления приводит к ряду интересных особенностей спектра пропускания дифракционных решёток [14].

Такие же аномалии проявляются и в идеально проводящих интегральных элементах [19], в частности, при сочленении идеально проводящих волноводов или при наличии неоднородностей в идеально проводящих волноводах. Это объясняется тем, что дисперсионное соотношение мод плоскопараллельного волновода c идеально-проводящими обкладками совпадает с дисперсионным соотношением плоских волн в разложении Рэлея.

В случае интегральных элементов, работающих в оптическом диапазоне частот, законы дисперсии падающих и рассеянных мод имеют более сложный вид. Поэтому аналоги аномалий Рэлея могут наблюдаться лишь случайно, когда две комплексные константы распространения падающей и рассеянной волны совпадут (при действительной или комплексной частоте). Появление такой ситуации на практике представляется достаточно маловероятным.

6.    Расчёт мод непериодической структуры

В соответствии с (2) моды структуры являются полюсами матрицы рассеяния, поэтому наиболее естественный подход к расчёту мод заключается в отыскании полюса матрицы рассеяния структуры. В простейшем случае расчёт полюса матрицы рассеяния сводится к численному нахождению комплексного корня уравнения

1 det S = 0. (10)

Отметим, что непосредственное решение уравнения (10) приводит к численной неустойчивости. В связи с этим для нахождения полюсов матрицы рассеяния было разработано несколько численноустойчивых методов [6, 3]. Отметим, что некоторые из методов работы [6] требуют вычисления производной матрицы рассеяния, что следует делать осторожно: при вычислении производной по конечноразностным формулам следует убедиться, что соответствующие моды в представлении поля над и под структурой упорядочиваются одинаково при разных значениях частоты [3].

Расчёт мод на основе полюсов матрицы рассеяния является наиболее универсальным подходом. Однако при этом подходе могут найтись не только все локализованные моды структуры, но и, возможно, «фиктивные» моды, локализованные в PML-слоях (англ. Berenger modes), не имеющие физического смысла. Таким образом, при расчёте мод как полюсов матрицы рассеяния приходится рассчитывать распределения поля всех мод, отбрасывая нефизичные.

Если нас интересуют только моды, непосредственно оказывающие влияние на спектр пропускания (рис. 1 в ), то целесообразно вычислять моды как полюсы коэффициента пропускания. В этом случае собственные частоты мод находятся численно как корни уравнения

1 T ( ω ) = 0. (11)

В качестве примера с использованием вышеизложенного метода были рассчитаны моды прямоугольного резонатора на металлической подложке (см. рис. 1 б ). В качестве металла рассматривалось серебро, диэлектрическая проницаемость которого описывалась моделью Лоренца–Друде [20]. Ширина резонатора составляла w =900 нм, высота – h =600 нм, диэлектрическая проницаемость материала резонатора – ε = 5,5, толщина металлического слоя – 200 нм. Моды рассчитывались в диапазоне частот Re toe |^1,0 x 10¹⁵; 1,6 x 10¹⁵ J c ^{- 1}. При этом рассчитывались только высокодобротные моды (Im toe [- 1,5 x 10¹⁴; 0 j c ^{- 1}). Частоты мод были рассчитаны как корни уравнения (11). При этом коэффициент пропускания T ( ω ) при комплексных аргументах вычислялся с использованием вышеизложенного алгоритма, основанного на методе фурье-мод в формулировке работ [7, 13, 17]. При расчёте использовалась N = 75×2+1 фурье-гармоника. Распределение электромагнитного поля мод, рассчитанное с использованием численно-устойчивого метода [11], приведено на рис. 3. Соответствующие комплексные частоты мод приведены в таблице. Отметим, что использование приближённого подхода из работы [3], в рамках которого разделение мод на падающие и рассеянные производится по знаку величины Re k z + Im k z , даёт неправильное распределение поля, которое резко возрастает вне области ступеньки.

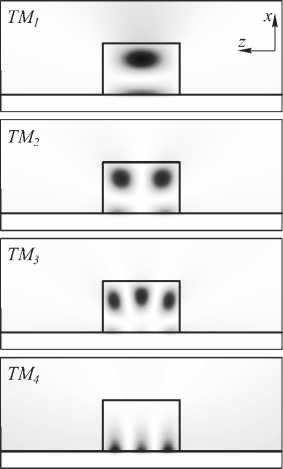
Рис. 3. Распределения поля | H_y |² TM-мод: TM 1 , TM 2 , TM 3 , TM 4

Табл. Параметры мод, рассчитанных предложенным методом и с использованием MEEP (в скобках)

Мода	to p , с - 1	Re X , нм	Q
TM 1	1,011 x 1015 - 1,092 x 1014i	1841,3	4,6
	(1,007 x 1015 - 1,092 x 1014i)	(1848,1)	(4,6)
TM 2	1,201 x 1015 - 4,702 x 1013i	1565,7	12,8
	(1,217 x 1015 - 4,241 x 1013i)	(1545,9)	(14,3)
TM 3	1,505 x 1015 - 3,932 x 1013i	1250,8	19,1
	(1,503 x 1015 - 3,871 x 1013i)	(1252,3)	(19,4)
TM 4	1.290 x 1015 - 1.320 x 1014i	1444,8	4,9
	(1,283 x 1015 - 1,312 x 1014i)	(1453.2)	(4.9)
TE 1	1,049 x 1015 - 8,939 x 1013i	1782,9	5,9
	(1,050 x 1015 - 8,569 x 1013i)	(1782,3)	(6.1)
TE 2	1,068 x 1015 - 4,222 x 1013i	1761,5	12,7
	(1,064 x 1015 - 4,383 x 1013i)	(1767,9)	(12,2)
TE 3	1,466 x 1015 - 7,423 x 1013i	1281,7	9,9
	(1,464 x 1015 - 6,427 x 1013i)	(1283.9)	(11.4)
TE 4	1,241 x 1015 - 4,208 x 1013i	1516,2	14,7
	(1,243 x 1015 - 5,656 x 1013i)	(1512,5)	(11,0)
TE 5	1,522 x 1015 - 2,332 x 1013i	1237,1	32,6
	(1,521 x 1015 - 2,240 x 1013i)	(1238,2)	(34,0)

Наибольшее влияние на спектр оказывают моды (б) и (в). Эти моды обладают наибольшей добротностью, и их возбуждение обуславливает резкие минимумы в спектре пропускания на частотах to ~ 1,2x10 15 c^-1, го ~ 1,5x10 15 c^-1 (см. рис. 1 в ).

Из распределения поля видно, что моды TM 1 , TM 2 и TM₃ являются модами прямоугольного резонатора порядков 1, 2, 3 соответственно. Мода TM₄ является плазмонной модой типа Фабри–Перо. Распределение поля снаружи резонатора показывает, что мода TM 1 рассеивается в волну, направленную по нормали к поверхности, в то время как моды TM₂ и TM₃ рассеиваются по нескольким направлениям. Мода TM 4 по большей части рассеивается в поверхностный плазмон-поляритон. Таким образом, анализ распределения поля моды позволяет определить направления (каналы) рассеяния электромагнитной энергии. Используя теорему взаимности, можно показать, что эти же направления определяют возможные направления, из которых рассматриваемую моду можно возбудить [21]. Более того, метод фурье-мод позволяет численно рассчитать коэффициент связи моды с плазмон-поляритоном. Данный анализ важен при создании элементов нанофотоники для эффективного возбуждения волноводных мод и поверхностных плазмон-поляритонов [21]. В частности, предложенный в настоящей работе метод расчёта мод в совокупности с теоремой взаимности были применены авторами в задаче управляемого возбуждения поверхностных плаз-мон-поляритонов с помощью прямоугольных резонаторов из магнитооптического материала [22].

Как было отмечено выше, расчёт мод на основе уравнения (11) позволяет получить только те моды, которые можно возбудить рассматриваемой падающей модой. В настоящей задаче в качестве падающей волны выбран поверхностный плазмон-поляритон, следовательно, набор рассчитанных мод ограничен только TM-модами. Кроме ограничений по поляризации, выбранный подход может накладывать ограничения на симметрию рассчитываемых мод [2, 5]. Для расчёта всех мод структуры в рассматриваемом диапазоне частот были рассчитаны моды как полюсы матрицы рассеяния. В результате расчёта были получены все моды рис. 3, а также TE-моды, изображённые на рис. 4. Из распределения поля TE-мод видно, что они не связаны с поверхностными плазмон-поляритонами и их рассеяние происходит в свободное пространство над структурой.

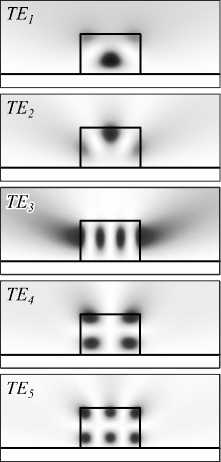
Рис. 4. Распределение поля |E_y|² TE-мод: TE 1 , TE 2 , TE 3 , TE 4 , TE

В таблице приведены комплексные частоты, длины волны и добротности всех рассчитанных мод структуры. Для сравнения в скобках указаны те же величины, рассчитанные с использованием пакета MEEP [23] и библиотеки harminv, которые реализуют метод FDTD и метод работы [10] соответственно. Данные приведённой таблицы подтверждают правильность работы предложенного метода. Отличия частот мод, рассчитанных предложенным методом и пакетом MEEP, не превышает 1,4 %. Отметим, что разработчики пакета MEEP 1.3 указывают на низкую точность расчёта низкодобротных (Q<50) мод. Также отметим, что метод работы [10] не позволяет рассчитать распределение поля отдельно взятой моды, в то время как предложенный в настоящей работе метод позволяет это сделать (см. рис. 3–4).

7.    Расчёт мод намагниченной непериодической структуры

В рассмотренной выше структуре особенности в спектре пропускания объясняются возбуждением лишь TM-поляризованных мод. В случае, если резонатор выполнен из магнитооптического материала, плазмон-поляритон может возбудить TE-поляризо-ванные моды структуры. В этом случае спектры пропускания намагниченной и ненамагниченной структуры могут существенно отличаться.

В качестве примера рассмотрим прямоугольный резонатор (см. врезку к рис. 5 а ) со следующими параметрами: ширина w = 2650 нм, высота h = 2260 нм. Резонатор расположен на серебряной подложке, диэлектрическая проницаемость которой задаётся моделью Лоренца–Друде [20]. Диэлектрическая проницаемость резонатора задаётся следующим тензором:

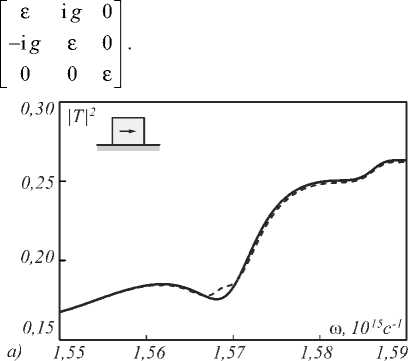
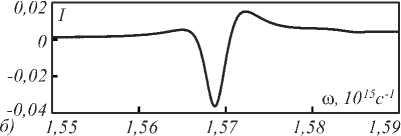
Рис. 5. Спектр пропускания намагниченной (пунктир) и ненамагниченной (сплошная линия) структур (а), величина интенсивностного эффекта (13) (б)

Данный вид тензора соответствует намагничиванию резонатора в направлении оси z . При расчёте использовались следующие параметры тензора (12): £ = 5,0625+4,3 x 10^-4i, g = 0,015319-3 х 10^-5i. Данные параметры соответствуют материалу висмутзамещённый диспрозиевый феррит гранат [24].

На рис. 5 а представлены спектры пропускания намагниченного и ненамагниченного резонаторов. В окрестности длины волны ю = 1,569 х 10¹⁵ с^-1 коэффициенты пропускания намагниченного и ненамагни-ченного резонаторов существенно отличаются. На рис. 5 б представлена величина магнитооптического эффекта, представляющая собой относительное изменение интенсивности прошедшего плазмон-полярито-на, обусловленное намагничиванием образца:

I = ( T ( g )|² - T ( 0 )1²)/ T ( 0 )1² , (13) где | T ( g )|² и | T (0)|² – интенсивность прошедшего плаз-мон-поляритона для намагниченного и ненамагничен-ного резонаторов соответственно. Из рис. 5 б видно, что при частоте и = 1,569 x 10 5 с^-1 намагниченность резонатора существенно влияет на её коэффициент пропускания, а величина магнитооптического эффекта

• (13)    достигает значения | I | = 0,036. Отметим, что вдали от резонанса (нерезонансный) магнитооптический эффект на порядок меньше, чем на указанной частоте.

Для объяснения данного эффекта были рассчитаны моды структуры. В окрестности частоты и =1,569 x 10 5 с^-1 в структуре существует TE-мода с комплексной частотой to p =1,5667x10¹⁵-3,8308x10¹²i с^-1. Данная мода не возбуждается в ненамагниченной структуре, но при намагничивании происходит преобразование поляризации, что приводит к возбуждению указанной моды и возникновению резонансного магнитооптического эффекта [5]. Отметим, что добротность данной моды на порядок выше добротности мод, рассмотренных в разделе 5. Это достигается большим объёмом резонатора и приводит к большой величине магнитооптического эффекта на рис. 5 б .

Заключение

В настоящей работе предложено обобщение метода фурье-мод, предназначенное для расчёта локализованных мод интегральных оптических резонаторов. Обобщение заключается в строгом построении аналитического продолжения матрицы рассеяния, что позволяет рассчитывать моды непериодических структур как полюсы матрицы рассеяния. Строгое построение аналитического продолжения особенно важно при расчёте низкодобротных мод. Представлены результаты расчёта локализованных мод диэлектрической структуры на металлической подложке. При этом показано, что комплексные частоты мод соответствуют резонансным особенностям в спектре пропускания и близки к частотам мод, рассчитанным на основе метода FDTD. Показано, что расчёт мод непериодических структур позволяет объяснить резонансные магнитооптические эффекты, возникающие при прохождении поверхностного плазмон-поляритона через намагниченный резонатор.

В настоящей работе задача расчёта мод сводится к расчёту полюсов матрицы рассеяния. Альтернативным является подход, представленный в работах [11, 25], где моды рассчитываются из условия формирования резонансов типа Фабри–Перо. Отметим, что предложенный в настоящей работе метод построения аналитического продолжения матрицы рассеяния также может быть применён для обобщения метода работ [11, 25].

Работа выполнена за счёт гранта РНФ (14-19-00796).