О применении метода стробоскопических выборок при изучении квадрупольного возбуждения и квадрупольного резонанса

В работе [1] предлагается новая теория для описания квадрупольного резонансного возбуждения ионов в квадрупольных ВЧ электрических полях. Она базируется на анализе методом возмущений огибающих стробоскопических выборок координат и скоростей ионов в радиочастотном квадруполе, который был предложен в [2]. В частности, из предложенной теории очень просто выводится, что расщепление исходной зоны устойчивости происходит по изолиниям в = const диаграммы стабильности уравнения Матьё, а фаза квадрупольного возбуждения не влияет на образование дополнительных полос и островков устойчивости и неустойчивости (результаты, полученные ранее для частного случая рациональных частот возбуждения, и притом гораздо более сложным способом [3, 4]). Кроме того, важным моментом является обобщение теории квадрупольных возбуждений на случай произвольных частот, тогда как до сих пор эффект квадрупольных возбуждений в полном объеме анализировался лишь для частот, находящихся в рациональном отношении к базовой частоте радиочастотного квадруполя (особенность используемого для анализа проблемы математического аппарата матриц монодромии).

Однако при более внимательном рассмотрении в работе [1] обнаруживаются досадные логические неувязки, которые ставят под сомнение надеж- ность полученных формул. Рассмотрим подробнее этот вопрос.

Основой теории [1] является теория огибающих для стробоскопических выборок координат и скоростей траекторий ионов в квадрупольном радиочастотном поле, которая была разработана в [2]. В рамках этой теории рассматривается движение ионов с массой m и зарядом e в квадрупольном радиочастотном поле с потенциалом

Ф ( x , y ) = F ( t )---^                   (1)

r 0 ²

для частного случая F ( t ) = U + V cos О t , где x , y — декартовы координаты; r ₀ — радиус окружности, вписанный между гиперболическими электродами; U — постоянная составляющая напряжения, приложенного к электродам; V — амплитуда синусоидального радиочастотного напряжения, приложенного к электродам; О — круговая частота радиочастотного напряжения. В безразмерных переменных ^ = О t /2 , a = 8 eU ( m m О ² r ₀ ² ) , q = 4 eV /( m О ² r ₀ ² ) движение ионов в рассматриваемом поле описывается парой уравнений Матьё [5, 6] с хорошо известными областями стабильности и нестабильности:

x "( ^ ) + ( a + 2 q cos2 ^ ) x ( ^ ) = 0,            (2)

y "( £ ) - ( a + 2 q cos2 £ ) y ( ^ ) = 0.            (2а)

Эти уравнения являются частным случаем систем линейных обыкновенных дифференциальных уравнений с периодически меняющимися во времени коэффициентами, теория которых достаточно хорошо исследована [7–14].

Рассмотрим движение по координате X . В рамках теории [2] анализируется поведение стробоскопических выборок координат и скоростей x_n = x ( nT ) , v_n = v ( nT ) = x ' ( nT ) , где T = п — безразмерный период приложенного радиочастотного напряжения. Дискретные отсчеты x_n , v_n подчиняются рекуррентному матричному уравнению

зоны стабильности, где в ~ 1, в работе [2] используются знакопеременные стробоскопические биения x _n , v _n , которые определяются по формулам x n = ( — 1 ) " x_n , v_n = ( — 1 ) " v„ , подчиняются рекуррентным матричным уравнениям

f ^x"

V v "

— M

(x xn—1

V v n — 1

= ( — 1 ) ² M ²

f X 1

n — 2

V v n — 2

= ( — 1 ) " M "

(x x0

V v 0

x

" | = M

I v n )

x

" - 1 | = M²

I v n - 1 )

x

" — 2

< v n — 2

= M"

x

⁰ | ,

I v 0 )

и для которых, согласно [2], гладкая синусоидальная огибающая X ( n ) подчиняется приближенному дифференциальному уравнению

где x0 , v0 — начальные значения координат и скоростей, a M =

f m xx

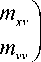
— так называемая

< m vx

матрица монодромии для линейного дифференциального уравнения с периодическими коэффициентами, соответствующая уравнению (2) (см. [1, 2, 11–15]).

Матрица монодромии играет важную роль при анализе уравнений движения в радиочастотных полях. В частности, от значения следа мат- рицы Tr = mxx + myy зависит устойчивость (если

— 2 < Tr <+ 2) или неустойчивость (если Tr <— 2 или Tr >+ 2) движения ионов. Для устойчивого режима движения важную роль играет безразмерный параметр Флоке β , вычисляемый из условия

2cos пв = Tr, лежащий в диапазоне 0 <  в <  1

и определяющий для ионов круговую частоту секулярных колебаний, в безразмерных координатах равную to s = в (см. [15]). Определитель матрицы монодромии равен единице (следствие закона сохранения фазового объема).

В работе [2] для стробоскопических отсчетов xn , vn конструируется гладкая синусоидальная огибающая X (n), V (n) и выводится приближенное дифференциальное уравнение

d2 X (n)     ,           ,

— 2 + 2 ( 1 — cos пв ) X ( " ) = 0.

Это уравнение интерпретируется как секулярные колебания стробоскопических отсчетов и используется в [2] для описания движения ионов в радиочастотном квадруполе по координате Y вблизи вершины зоны стабильности, где в ~ 0. Для описания же движения ионов в радиочастотном квадруполе по координате X вблизи вершины

d2 X (")

— 2 ' + 2 ( 1 + cos пв ) X ( " ) = 0 .

(В какой степени приближенные уравнения (4), (6) действительно справедливы, разбирается в публикациях [16–18])

Аналогичным образом разбирается движение иона по координате Y , где происходит изменение знака у безразмерных параметров a , q , а матрица монодромии M должна будет вычисляться в соответствии с уравнением (2а). С математической точки зрения описания движения с помощью секулярных стробоскопических отсчетов и с помощью биений стробоскопических отсчетов полностью эквивалентны друг другу, и какое из них использовать в конкретном случае — в значительной степени вопрос удобства математических выкладок при рассматриваемых значениях параметра β .

На основании уравнений (4) и (6) в работе [2] выводятся оценки для глубины псевдопотенци-альной ямы по координате Y и по координате X в окрестности вершины первой совместной зоны стабильности для линейного радиочастотного квадруполя. Следует отметить, что уравнения (4) и (6) являются более чем приближенными и имеют смысл только при в ~ 0 и в ~ 1. Этот вопрос анализируется в работах [16–18], где показано, что точное дифференциальное уравнение для синусоидальной огибающей X (n) секулярных стробоскопических отсчетов имеет вид d2X n

+ ( пв ) X ( " ) = 0,             (7)

d n ²

а точное дифференциальное уравнение для синусоидальной огибающей X (n) биений стробоскопических отсчетов имеет вид dXn) + (n(1 - в ))2 X (n ) = 0.          (8)

Уравнение (4) в окрестности в ~ 0 совпадает с уравнением (7) с точностью до кубических членов разложения по малому параметру β . Соответственно уравнение (6) в окрестности в ~ 1 совпадает с уравнением (8) с точностью до кубических членов разложения по малому параметру 1 - в . Отсюда, в частности, следует, что оценки для псевдопотенциальной ямы в окрестности вершины первой совместной зоны устойчивости линейного радиочастотного квадруполя, полученные в [2], справедливы лишь с точностью до кубических членов и имеют смысл лишь в окрестности вершины совместной зоны стабильности, где в ~ 0 для движения по координате у и в ~ 1 для движения по координате x . По-видимому, следует ожидать аналогичные неточности и при использовании этих уравнений при анализе эффекта квадрупольного возбуждения в работе [1]. Подробности вывода точных уравнений (7), (8) для огибающих стробоскопических выборок и сравнение их с приближенными уравнениями (4), (6), полученными в [2], приводятся в [16–18].

При наличии квадрупольного возбуждения функция F (t) для электрического потенциала (1) имеет вид F (t) = U + V cos Оt + Vex cos (rot + a), где Vex — амплитуда квадрупольного возбуждения, ω — круговая частота квадрупольного возбуждения, α — начальная фаза квадрупольного возбуждения. В таком случае уравнения для движения ионов принимают вид x "(%) + (a + 2 q cos 2^) x (5 ) =

= - ² q ex cos ( 2 V^ ^{+ a} ) ^x ( ^ ) ,                  (9)

У "( ⁵ )^-( a + ² q cos ^{2 5} ) у ( ⁵ ) =

= ^{+ 2} q ex cos ( ^{v + a} ) У ( 5 ) ,                (9а)

где v = ГО О , а q_ex = 4 eV ex /( m О ² r ₀ ² ) считается малым параметром, что позволяет анализировать уравнения (9), (9а) с помощью методов теории возмущений. Известно, что в зависимости от значений параметров ν и q_ex происходит сложное расщепление исходной диаграммы стабильности на дополнительные полосы стабильности и нестабильности [4], где число полос нестабильности зависит от параметра ν , а ширина полос нестабильности управляется параметром q_ex .

В работе [1] показано, что с учетом членов первого порядка, полученных методом теории возмущений для уравнения (9), секулярные стробоскопические отсчеты подчиняются матричному уравнению

x n | = Mn I vn J

Г x n - 1

V v n - 1

= ( M + C cos ( 2 nvn

- a ) - S sin ( 2 nvn

—

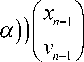
, (10)

где M — матрица монодромии для уравнения Матьё с нулевой правой частью, а C и S — вспомогательные постоянные матрицы. Поскольку для гладкой огибающей стробоскопического ре- шения матричного уравнения

x n | = M

V v n J

x n-1

V v n - 1

с постоянной матрицей справедливо приближенное уравнение (4), которое можно записать в виде d² X ( n )/d n ² + 2 ( 1 - s ) X ( n ) = 0, где s = Tr/2 =

= (mxx + mvv)/2 — половина следа матрицы M , то для матричного уравнения (10) с меняющейся в зависимости от индекса n матрицей авторами работы [1] делается смелый вывод, что гладкая огибающая стробоскопических отсчетов (10) подчиняется похожему дифференциальному уравнению d2X(n)/dn2 + 2(1 -sn)X(n) = 0, где sn — половина следа матрицы Mn . Соответственно огибающая биений xn =(-1)n x„, vn =(-1)nvn для матричного уравнения (10), согласно утверждению авторов работы [1], подчиняется дифференциальному уравнению d2 X (n)/dn2 + +2 (1 + sn) X (n ) = 0.

До этого шага выкладки авторов вполне корректны (за исключением того факта, что для получения более точных результатов вместо приближенного уравнения (4) следует использовать точное уравнение (7), а вместо приближенного уравнения (6) — точное уравнение (8)). Однако данный шаг оказывается не только методически и логически необоснованным и, вообще говоря, слабо связанным с предшествующими выкладками, но, что гораздо опаснее, с большой вероятностью он может оказаться вообще неверным по отношению к получаемым на выходе результатам. Действительно, рассмотрим матричное уравнение Г xn ) Г xn-1 )

| = M | с выбранными для тестового V vn J V vn-1 J примера матрицами M n , определенными как

M2 = = Ma = 2k       a cos пв - ца sin пв

C(V ^Х а ) 7^{1 + Ц} sin ^пв

M 2 к+1 = Mb = cos пв — ць sin пв

c(V ^X b )71 + Ц sin пв

Л а 71 + Ц 2 sin пв cos пв + ц_а sin пв

л

Л 71 + Ц ь sin пв cos пв + ц_ь sin пв

л

где параметр β фиксирован и лежит в диапазоне 0 < в < 1, а параметры Ла, Ль, ца, ць пока остаются неопределенными. (По сути в этом примере матрицы M n представляют собой матрицы моно- дромии, параметризованные с помощью параметров β , λa , λb , µa , µb [15, 19–21], которые попе- ременно переключаются между двумя группами параметров, не связанными друг с другом.) След всех матриц Mn постоянен и равен 2cosπβ . Это означает, что согласно предлагаемой в [1] логике рассуждений гладкая огибающая стробоскопиче-

(x xn - 1

x n | = Mn

I v n 7

ских отсчетов

должна удовлетво-

V v n - 1

рять уравнению d ² X ( n ) /d n ² + 2 ( 1 - cos пв ) X ( n ) = 0

при использовании приближенного уравнения (4) и уравнению d2X(n)/dn2 + (пв)2 X(n) = 0 при использовании точного уравнения (7). Также гладкая огибающая биений стробоскопических отсче- тов, соответствующих матричному уравнению ' xn I ( -1I

_ I = -Mn _ I, должна удовлетворять уравне-V vn 7 _ V vn-17 _ нию d2X (n)/dn2 + 2 (1 + cos пв) X (n ) = 0 при использовании приближенного уравнения (6) и уравнению d2X(n)/dn2 +(п (1 - в))2 X(n) = 0 при использовании точного уравнения (8).

Однако, если только параметры λa , λb , µa , µb для матриц (11) не подобраны специальным образом, то указанные уравнения не совпадают с правильными уравнениями для огибающих стробоскопических выборок даже для малых величин β и (1 - в). Действительно, если рассматривать стробоскопические отсчеты

x n = Mn

V v n 7

(x xn-1

V v n - 1

через

один отсчет, то для определенных, согласно (11), матриц M n будет выполнено соотношение f xn I        xn-2 I

I = M c I с постоянной матрицей

V v n 7       V v n - 2 7

Mc = MbMa . Тогда огибающая Xc (n) стробо- скопических отсчетов xn , рассматриваемых через один отсчет, будет удовлетворять приближенному уравнению d2 Xc (n)/dn2 + 2 (1 - sc) Xc (n ) = 0, где sc — половина следа матрицы Mc , и точному уравнению d2Xc (n)/dn2 +(пвс )2 Xc (n) = 0, где cos пвс = sc. Половина следа матрицы Mc равна величине sc = cos2 (пв) + цаць sin2 (пв)-

- ^Л + ^{Л 1 +} ц 2 V ^{1 +} ц 2 ^sin 2 ( ^пв ) , 2 λ_aλ_b

и это выражение радикальным образом отличается от тех частот, которые входят в уравнения гладких огибающих стробоскопических отсчетов, согласно рассуждениям авторов работы [1], даже с учетом удвоения секулярных частот и частот биений при удвоении шага стробоскопической выборки. Более того выражение (12) при некотором специальном выборе параметров λa , λb , µa , µb может выйти за пределы диапазона -1 < sc <+1, что означает, что матричное уравнение

x n I = Mn

V v n 7

x n-1

V v n - 1

потеря-

ет устойчивость — ситуация, невозможная для матриц вида (11), если придерживаться логики работы [1]. (Заметим, что некоторые случаи расхождения между теорией и численными результатами, на которые обращают внимание авторы работы [1], могут быть связаны именно с этой тон- костью при перемножении матриц, а не с поправками более высокого порядка для формул теории возмущений, как это объясняют авторы работы [1].)

Для решения поставленной задачи нет необходимости использовать столь запутанные и не слишком хорошо обоснованные преобразования, имея конечной целью свести ее к задаче исследования устойчивости решений уравнения Матьё с готовым решением. Вся нужная информация уже есть в приближенных решениях уравнений (9) и (9а), которые получаются в [1] с помощью стандартных методов теории возмущений:

x(^)Lfu1 (^) u2 (^)

V v ( ^ ) J V u;( ^ ) u ‘ ( ^ ) 7

X

X

¹ -^ ^{f ( т} ) u 1 ^{( т} ) u 2 ^{( т} ) ^{d T} _t ' J ^{4 f ( Т} ) u ^{2 ( T} ) ^{d T}

J4 f (t ) u2 (t ) dT

¹ ^ ^f ( ^T ) u 1 ^T ) u 2 ^T ) ^{d T},

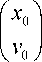
Здесь x ( 4 ) и v ( 4 ) = x '( 4 ) — приближенное решение уравнения (9) с ненулевой правой частью; и₁ ( 4 ) и и 2 ( 4 ) — фундаментальные решения однородного уравнения (2), удовлетворяющие начальным условиям и₁ ( 0 ) = 1, и [ ( 0 ) = 0, и 2 ( 0 ) = 0, и ‘ ( 0 ) = 1; f ( 4 ) = - 2 q_ex cos ( 2v4 + a ) — малое возмущение в правой части уравнения (9); x ₀ и v ₀ — начальная координата и начальная скорость. Решение для (9а) отличается от решения для (9) лишь заменой x ( 4 ) на у ( 4 ) , изменением знака у безразмерных параметров a , q , q_ex и использованием для и ( 4 ) , и ₂ ( 4 ) фундаментальных решений уравнения (2а).

Рассмотрим вопрос, как в рамках формулы (13) можно описать появление внутри зоны устойчивости уравнения Матьё (2) полос неустойчивости, индуцированных в соответствии с уравнением (9) дополнительным квадрупольным возбуждением. Устойчивое решение уравнения Матьё (2) можно представить с помощью матрицы Флоке — Ляпунова [20, 21] в виде

где β , λ , µ — параметры, являющиеся функциями безразмерных параметров a , q , а L_xx ( 4 ) , L xv ( ⁴ ) , L vx ( ⁴ ) , L vv ( ⁴ ) ^— периодические функции с периодом T = п , в первом приближении имеющие вид

L xx ( 4 ) » 1 + A ( 1 - cos 2 4 ) + - , L xv ( ^ ) « B sin2 ^ + - , L vx ( ^ ) « C srn2 £ + - , Lw ( ^ ) « 1 + D ( 1 - ™s2 £ ) + -

(где параметры A , B , C , D также являются функциями безразмерных параметров a , q ). Поэтому фундаментальные решения u ₁ ( ^ ) , и ₂ ( ^ ) для уравнения (2) приобретают вид

^u 1 ( ^ ) = L xx ( ^ )( ^{cos в}^ - ^ ^{sin в}^ ) ⁺

+ L x , ( 4 ) ( - ( 1 ² ) Jb + ^ ^Tsin в4 ) , u 2 ( ⁴ ) = ^Lxx ( ⁴ ) M ^{1 +} ^ 2 sin ^{в4 +}

+ L xv ( 4 )( cos в4 + ^ sin в4 ) ,

x * ^{( 4} ) )Г u ^{1 ( 4} ) ^{и 2 ( 4} )Y x 0 ) ( v * ( 4 ) J ( u ‘ ( 4 ) и 2 ( 4 )Л v 0 J

в котором нет неизвестных функций, а имеются только известные константы, извлекаемые из уравнения (2) с помощью конструктивных вы-

X

L xx ^{( 4} )   L xv ⁴ ) )

tLvx (4 )   L (4 )J

cos в^ - ^ sin в4

M 1 + Ц ² sin в4

(- ( 1 M ) jw sin в4 cos в4 + Ц sin в4 J

X

X

x 0

( ^v 0

числительных процедур.

При выполнении в (13) умножения на матрицу фундаментальных решений

ф(4 ) =

" u 1 ^{( 4} ) u 2 ^{( 4} )^ ( u ‘ ( 4 ) и ‘ ( 4 ) J

результат остается ограниченным, в силу того что рабочая точка выбрана в пределах зоны устойчивости уравнения Матьё. Поэтому неограниченный рост решения ( x ( 4 ) , v ( 4 ) ) может быть связан

только с ростом матрицы

^- J 0 ⁴ f ^{( т} ) u 1 ^{( t} ) u 2 ^{( t} ) d ^{T -} J 0 ⁴ f ^{( t} ) u 2 ^{( t} ) d ^T _t ⁺ J ₀ ^{4 f} ( ^T ) u ² ( ^T ) ^{d T} + J 0 ^{4 f} ( ^T ) u 1 ( ^T ) u 2 ( ^T ) ^{d T} ^

После аккуратного выполнения в (18) внут- и f ( 4 ) = - 2 q ex cos ( 2v4 + a ) , а также преобразова-ренних умножений с учетом условий (15), (16)   _{ния п}р_оизвед_ений _тр_{игономет}р_{ических} фу_нкц_ий

в тригонометрические суммы под знаками интеграла образуются суммы тригонометрических членов со следующими частотами:

2v , 2 ± 2 v , 4 ± 2 v , 2 в ± 2 v , 2 ± 2 в ± 2 v , 4 ± 2 в ± 2 v .

Если все частоты (19) не равны нулю, то после выполнения в формуле (18) интегрирования получится тригонометрическая сумма, ограниченная по амплитуде на всем интервале изменения безразмерного времени ξ . Однако, если какие-то из выражений (19) обращаются в ноль, то в матрице (18) образуются аддитивные члены, пропорциональные безразмерному времени ξ . То есть в этих и только в этих случаях с ростом безразмерного времени ξ будет наблюдаться неограниченный рост матрицы (18) и соответственно неограниченный рост решения (13).

Естественно, это утверждение будет справедливо ровно той мере, в которой приближенное выражение (13) описывает истинное поведение решений уравнения (9). Например, примéним этот же метод возмущений к уравнениям с постоянными коэффициентами и нелинейной осциллирующей правой частью, которые получаются из системы уравнений первого порядка для уравнения (9) после умножения на периодическую матрицу L из метода Флоке—Ляпунова. Тогда можно увидеть, что неограниченный рост приближенных решений вследствие резонанса на секулярной частоте β следует ожидать в том числе и тогда, когда какая-либо из частот (19) совпадает с резонансной частотой ± в .

Полученный результат (нарушение устойчивости лишь в изолированных резонансных точках) противоречит результатам работы [4] о появлении при квадрупольном возбуждении полноценных полос нестабильности конечной ширины. Это противоречие отчасти устраняется следующим рассуждением. Матрица (18) стремится с ростом ξ к бесконечности, если какие-то из частот (19) в точности обращаются в ноль. Однако, когда какие-то из частот (19) близки к нулю, то знаменатели, получающиеся при интегрировании соответствующих тригонометрических членов, приводят к резкому увеличению амплитуды траекторий. Такие траектории ионов быстро выходят за пределы межэлектродного промежутка ± r₀ даже при незначительных отклонениях начальных условий от оси квадруполя. Данный эффект вполне заменяет собой полосы нестабильности, поскольку "вычищает" из объема квадруполя ионы со значениями параметра β , лежащими в определенных континуальных интервалах.

Если выбрать такое малое значение ε , что на расстоянии ± £ от оси квадруполя число ионов пренебрежимо мало, то можно рассчитать в явном виде положение и размеры полос квазинестабильности, для которых траектории, стартовавшие на расстоянии от оси квадруполя, которое превышает ε , оказываются за пределами межэлектродной апертуры ± r ₀. При этом необходимо учитывать не только эффект от матрицы (18), но и умножение в формуле (13) на матрицу (17). Если фронты резонансных пиков достаточно острые, то положение и ширина полос квазинестабильности будут слабо зависеть от конкретного значения малого параметра ε . Отметим, что при переходе от первого приближения теории возмущений (13) к поправкам более старшего порядка в соответствующих выражениях будут появляться более сложные произведения величин и 1 ( ^ ) , и ₂ ( ^ ) и f ( ^ ) , что приведет к появлению дополнительных полос квазинестабильности для уточненной модели.

Полученная модель правильно описывает на качественном уровне основные закономерности квадрупольного возбуждения. При увеличении параметра q_ex происходит уширение имеющихся полос нестабильности, но при этом их положение и их число остаются неизменными (эффект связан с тем, что параметр q_ex является множителем при f ( ^ ) и пропорционально масштабирует траектории матрицы (18), выводя за пределы апертуры ± r ₀ те траектории, которые ранее оставались в межэлектродном промежутке и лежали вблизи границы для полосы нестабильности). Границы полос нестабильности проходят по изолиниям параметра Флоке β (эффект следует из выражений (19) для частот тригонометрических членов и соответственно для знаменателей, описывающих высоту резонансных пиков). Положение и ширина полос нестабильности не зависит от фазы квадрупольного возбуждения, хотя вид траекторий ионов от нее зависит существенным образом (эффект связан с тем, что в выражениях (19) для частот тригонометрических членов и соответственно для знаменателей, описывающих высоту резонансных пиков, фаза квадрупольного возбуждения не участвует). Наконец при варьировании частоты ν квадрупольного возбуждения меняется число полос нестабильности, так как появляется возможность обнулять с помощью выбора параметра 0 <  в <  1 те выражения из списка (19), которые ранее в ноль не обращались.

С помощью похожих рассуждений можно проанализировать и такой любопытный и нетривиальный эффект от использования квадрупольного возбуждения, что при некоторых условиях на месте прежней зоны нестабильности могут возникать дополнительные полосы стабильности. Однако соответствующий анализ потребует применения матриц Флоке—Ляпунова для нестабильного движения [20, 21] и несколько более аккуратных выкладок, и его реализация выходит за рамки целей данной заметки.

К сожалению, описанная выше упрощенная модель квадрупольного возбуждения лишь имитирует возникновение новых зон нестабильности, заменяя полноценную неограниченность траектории и уход ее на бесконечность на гораздо более слабое условие — а именно, на локальный выход траектории иона за пределы фиксированной геометрической зоны, ограниченной электродами, при сохранении глобальной ограниченности рассматриваемой траектории некоторым предельно достижимым радиальным расстоянием. В то же время хорошо известно [4], что при квадрупольном возбуждении должны возникать полноценные дополнительные зоны устойчивости и неустойчивости, уводящие траектории ионов экспоненциально быстро на бесконечность. С физической точки зрения такое поведение траекторий ионов принципиальным образом не совпадает с описанной выше имитацией неустойчивости, при которой ионы время от времени возвращаются обратно в межэлектродную область пространства, чтобы через некоторое время (с полиномиальной скоростью убегания вместо экспоненциальной скорости убегания) снова уйти за ее пределы.

Насколько можно судить, этот не слишком обнадеживающий результат является следствием того факта, что при наличии резонансных явлений методы теории возмущений не должны применяться "в лоб" и требуют особой аккуратности. А именно: корректная схема применения методов теории возмущений для таких случаев, по всей видимости, должна выглядеть следующим образом: а) в правой части в явном виде выделяются компоненты, ответственные за резонансные эффекты; б) указанные компоненты присоединяются к основному уравнению и полученное уравнение решается как единое целое; в) остаток в правой части рассматривается как малая поправка, а решение неоднородного уравнения с малой поправкой в правой части конструируется с помощью методов теории возмущений, используя для этой цели полученное ранее базовое решение "резонансного" уравнения. К сожалению, выделение в правой части уравнения критических резонансных членов, причем в такой форме, для которой у итогового резонансного уравнения можно найти аналитическое решение, является скорее предметом математического искусства, чем готовой отработанной методологией (в качестве примеров см.

разбор теории параметрических резонансов в [22] и [14, 23]).

Как легко можно заметить, метод, использованный в работе [1], ограничивается вполне формальным и прямолинейным применением стандартной схемы теории возмущений, не обращая внимания на тонкости, связанные с резонансными эффектами. В силу этого полученная на выходе модель даже после устранения логических нестыковок не способна в полной мере отразить физику процессов, происходящих при квадрупольном возбуждении ионов, а лишь имитирует определенные аспекты данного явления. Фактически же теория [1], основанная на методе возмущений огибающих стробоскопических выборок координат и скоростей ионов в квадрупольном поле, претендует на решение лишь тех задач, которые в настоящий момент уже решены другими методами. Например, к таковым можно отнести определение положения полос нестабильности, описание движения ионов в квадрупольных полях под действием резонансного воздействия квадрупольных полей и так далее [3, 4].

Представляется, что в своем нынешнем состоянии теория, предложенная в [1], мало пригодна для практических приложений и что в силу этого для изучения тонких моментов квадрупольного резонанса будет надежнее и эффективнее напрямую использовать уравнения (9), (9а). Кроме того, тот факт, что из уравнений (13) после предлагаемых авторами математических преобразований получаются результаты, в исходной системе уравнений (13) напрочь отсутствующие, наглядно доказывает как методическую и логическую ошибочность используемого авторами подхода, так и ненадежность получаемых на этом пути результатов (см. также [16–18]).

Полезно отметить, что близкие по своей математической природе эффекты рассматриваются также в [24–27], а для квадрупольного возбуждения — в [28–30].

РЕЗЮМЕ

Приведенный анализ показывает, что в выкладках работы [1] имеются два важных пробела в логике рассуждений: а) нельзя применять метод возмущений в той форме, в которой его используют авторы работы, если предварительно не выделить в нелинейном возмущении члены, ответственные за параметрический резонанс (см. [22]); б) преобразования, используемые авторами, не могут не содержать существенной методической ошибки, поскольку в результате из системы уравнений (13) с дополнительными неустойчивостями в виде изолированных точек получаются неэквивалентные им уравнения с неустойчивостями в виде контину- альных полос. По-видимому, до устранения указанных недостатков вряд ли можно использовать итоговые формулы работы [1] при анализе поведения радиочастотных квадруполей.

Данная работа частично выполнена в рамках гос. задания № 075-00780-19-00 для ИАП РАН и гос. задания Минобрнауки России № 3.9506. 2017/8.9.