О применении пакета ANSYS для исследования деформирования здания с учетом трещинообразования

ДЕФОРМИРОВАНИЯ ЗДАНИЯ С УЧЕТОМ ТРЕЩИНООБРАЗОВАНИЯ

В работе исследуется модель образования трещин в хрупких материалах, представленная в конечно-элементном комплексе ANSYS. Тестирование модели при задании свойств материала различными способами рассматривается на задаче о шарнирно опертой балке, на основании которой выбирается наилучший способ приложения нагрузки и задания свойств материала. На следующем этапе исследуемая модель применяется к расчету трещинообразования в здании, выявляются наиболее неблагоприятные зоны и определяется характер и направление образовавшихся трещин.

Изучение эффектов, возникающих вследствие значительных неравномерностей осадок, например трещинообразования, на сегодняшний день является актуальной проблемой. Решение данных задач может дать ответ на вопрос о надежности, несущей способности и возможности дальнейшей эксплуатации зданий и сооружений.

Численная реализация поставленной задачи производилась в конечно-элементном комплексе ANSYS. Для учета нелинейных свойств бетона и кирпичной кладки использовалась модель Concrete, описывающая упруго-хрупкое поведение данных материалов. Модель Concrete реализует алгоритмы объемно-напряженного состояния бетона в соответствии с [1]. Данная модель допускает образование трещин (сколов) на площадке, нормальной к действующим главным напряжениям, при превышении данным главным напряжением заданного предела прочности на растяжение (сжатие).

Для дискретизации трехмерных областей использованы объемные восьмиузловые конечные элементы первого порядка с Лагранжевой аппроксимацией SOLID65. Такой элемент представлен на рис. 1.

Элемент SOLID65 используется для трехмерного моделирования объемных тел, имеющих или не имеющих арматуру. Объемный элемент имеет возможности образования трещин при растяжении и дробления при сжатии. Например, в расчетах железобетонных конструкций объемные возможности элемента могут использоваться для моделирования бетона, в то время как возможность учета арматуры применяется для моделирования свойств подкрепления конструкции. Элемент определяется восемью

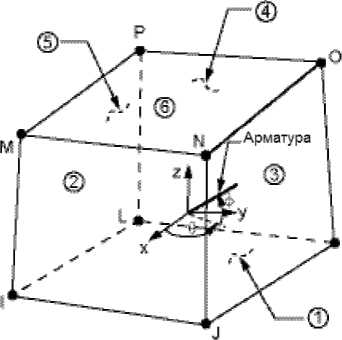
Рис. 1. Конечный элемент SOLID65. Геометрия

к

узлами, имеющими по три степени свободы: перемещения в направлении осей X, Y и Z. Также в элементе можно указать до трех направлений армирования [2].

Элемент железобетона аналогичен объемному элементу задач МДТТ с добавлением специальных возможностей образования трещин и скалывания. Самой важной особенностью этого элемента является использование нелинейных свойств материала. Бетон имеет возможность образования трещин (в трех ортогональных направлениях), скалывания, пластического деформирования и ползучести. Арматура имеет возможность растяжения и сжатия, но не сдвига, также поддерживает свойства пластического деформирования и ползучести.

Геометрия, расположение узлов и система координат элемента показаны на рис. 1. Элемент определяется восемью узлами и свойствами изотропного материала. К специальным возможностям элемента относятся: пластичность, ползучесть, образование трещин и сколов, большие перемещения и деформации, изменение жесткости при приложении нагрузок, рождение и смерть [3]. При образовании трещины в элементе можно посмотреть, в каком направлении она развивается и ее состояние: закрыта или открыта трещина.

Далее для демонстрации свойств элемента с возможностью трещинообразования рассмотрим задачу о шарнирно опертой балке, представленной на рис. 2. Исследуемая модель представляет собой шарнирно закрепленный брусок размерами 10 × 1 × 1 м, к центру которого по всей ширине приложено вертикальное перемещение. Для наглядности и лучшей сходимости решения нами был выбран кинематический способ приложения нагрузки. Во всех примерах прикладывалось одинаковое перемещение u_y =- 0,01м.

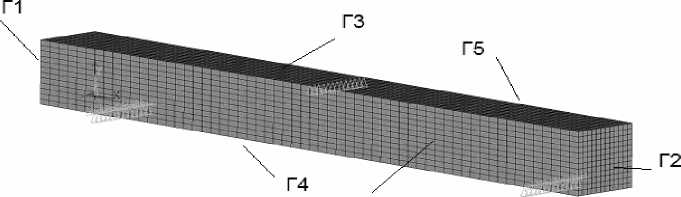
Гб

Рис. 2. Свободно опертая балка. Закрепление и нагрузка

Трехмерная модель балки занимает объем V , ограниченный поверхностью Г = Г1 ∪ Г2 ∪ Г3 ∪ Г4 ∪ Г5 ∪ Г6 (см. рис. 2). Система балки отнесена к прямоугольной декартовой системе координат, начало которой расположено в левом дальнем углу плоскости Г4 (нижняя плоскость).

Для определения напряженно-деформированного состояния имеем следующую систему уравнений.

• ■    Уравнения равновесия:

σ _{ij , j} ( x ) +ρ ( x ) F_i = 0, x ∈ V ,                              (1)

где x – радиус-вектор пространственного положения частицы, ρ ( x ) – плотность материала, ρ F_i – компоненты вектора внешних массовых сил.

Здесь и далее по умолчанию запятая с индексом означает частную производную по соответствующей координате xi; индексы при компонентах тензоров, набранные малыми латинскими буквами, принимают значения от 1 до 3. По повторяющемуся индексу (называемому немым индексом) предполагается суммирование также от 1 до 3, если не оговорено другое.

■ Геометрические соотношения (соотношения Коши).

Полагаем, что во всех точках деформируемой области деформации будут

достаточно малыми: eij(x) = 2(ui, j(x) + uj,i(x)), x e V,                              (2) где ui – компоненты вектора перемещения.

• ■    Физические (определяющие) соотношения.

Определяющие соотношения МДТТ для случая линейной связи между напряжениями и деформациями имеют вид обобщенного закон Гука:

° у = С ум ^{( x ) e} ki , ^{x e} V ,                             ⁽³⁾

где С _ijkl – компоненты тензора упругих констант.

• ■    Граничные условия заданы в перемещениях в виде шарнирного опирания по нижней поверхности и вертикальных перемещений в центре верхней поверхности по всей ширине балки. Остальные поверхности свободны от нагрузок:

ux (x) = 0, uz(x) = 0,                      x = 0,9L e Г4, uy(x) = -0,001-L,                        x = L/2e Г3,             (4)

ux(x) = 0,uy(x) = 0, uz(x) = 0,             x = 0,1 Le Г4, где L – длина балки.

° i ^{( x )} n j ^{( x )} = 0.

Также учитывалось нелинейное поведение, связанное с изменением состояния материала конструкции (появление трещин, раскрашивание). Жесткость в таких случаях меняется скачком и может зависеть непосредственно от нагрузки или определяться некоторыми внешними причинами. При этом учитывались такие характерные виды разрушения бетона и кирпичной кладки, как раскалывание и раскрашивание .

Растрескивание материала или появление «трещины» в плоскости, перпендикулярной одной из координатных осей, приводит к падению жесткости материала в данном направлении. Под «трещиной» понимается образование в бесконечно малом элементе среды зоны со сниженными механическими характеристиками в результате накопления повреждений [5].

В центре балки приложено перемещение по всей ширине (см. рис. 2), армирование отсутствует, но с помощью таблиц данных введены нелинейные свойства бетона (учтена зависимость модуля упругости материала от деформации (рис. 3)).

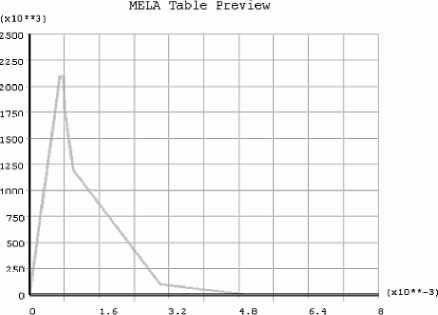
В          2.4         4           5.6         7.2

FPS

Рис. 3. Кривая зависимости напряжений и деформаций

На рис. 4–6 приведены изополя деформаций ε _y , главных напряжений σ ₁ и вертикальных перемещений u_y . Из рис. 5 видно, что в зоне образования трещины напряжения равны нулю, таким образом, «треснувшие» элементы перестают работать и нагрузка перераспределяется на соседние элементы.

Рис. 5. Напряжения σ ₁ , Па, σ _max = 15 МПа

Рис. 4. Деформации ε _y

Рис. 6. Изополя вертикальных перемещений u _y , м, u _max = 0,01м

В результате приложения нагрузки в зонах наибольших растягивающих напряжений образовались трещины. Так как приложенная нагрузка действует в одном направлении, то, как и следовало ожидать, все трещины перпендикулярны действию этой нагрузки, т.е. перпендикулярны площадке главных напряжений σ ₁ . На рис. 7 показаны картины трещин при различных сгущениях сетки. Самая глубокая трещина на рис. 7, в, так как в этом случае самая мелкая сетка, следовательно, жесткость конечноэлементной конструкции ниже.

Также было рассмотрено поведение данной тестовой модели при задании различных свойств, т.е. помимо задания диаграммы деформирования материала решались задачи при учете опции армирования конечного элемента и без учета каких-либо свойств, задавались только пределы прочности материала на сжатие и разрыв (рис. 9, 10). На рис. 8 показано направление армирующего материала.

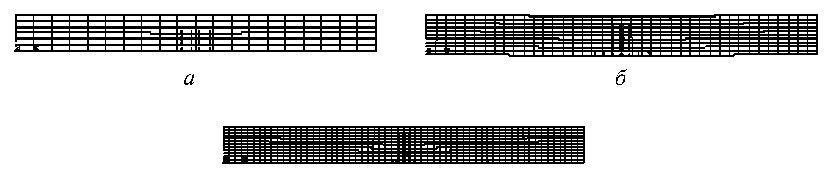
в

Рис. 7. Картина трещин в зависимости от размера КЭ сетки: а – при 720 элементах; б – при 4000 элементах; в – при 8640 элементах

Рис. 9. Картина трещин при учете армирования (4000 элементов)

Рис. 8. Направление армирования

Рис. 10. Картина трещин при учете только пределов прочности материала

Результаты тестовых примеров показали, что выбранный конечный элемент чувствителен к размеру сетки и способу приложения нагрузки.

В качестве расчетной модели для исследования напряженно-деформированного состояния более сложной конструкции взято здание с фундаментом без моделирования грунтового массива, представленное на рис. 11. Влияние основания учитывается с помощью кинематических граничных условий, приложенных к фундаментной плите здания. Из-за неравномерности поля перемещений в здании начался процесс трещинообразования. Для упрощения модели и в силу того, что кирпичная кладка имеет более низкие прочностные характеристики, чем бетон, трещинообразование учитывалось только в материале кирпичной кладки.

Физико-механические свойства бетона и кирпичной кладки приведены в таблице [5].

Рис. 11. Геометрическая модель сегмента здания

Физико-механические характеристики материалов

Материал	Модуль упругости, МПа	Коэф-т Пуассона	Расчетное сопротивление растяжению, МПа	Расчетное сопротивление сжатию, МПа	Плотность, кг/м 3
Кирпичная кладка	750	0,25	0,21	9	1900
Бетон	23500	0,22	7,5	28,5	2800

Поскольку свойство трещинообразования для данной расчетной схемы учитывалось только в кирпичной кладке, на рис. 12 приведена картина распространения трещин для материала кирпичной кладки на уровне первого этажа здания. Чтобы избежать лишних концентраторов напряжений, из расчетной схемы были исключены оконные проемы.

Рис. 12. Картина и статус трещин в кирпичной кладке стен первого этажа:

– свойства материала не изменились;

– трещина открыта в направлении σ ₁ , в направлениях σ ₂ и σ ₃ отсутствуют

– трещина открыта в направлении σ1 , в направлениях σ2 и σ3 есть закрытые трещины

Из полученного напряженно-деформированного состояния можно судить о наиболее неблагоприятных зонах, в которых может развиваться трещина. С помощью пакета ANSYS был оценен характер (закрыта или открыта) и направление трещины. Таким образом, можно сделать вывод, что данная расчетная схема подходит для прогнозирования развития трещин в здании и выявления их локализации.