О применении разрывного метода Галёркина для решения двумерного уравнения переноса на ортогональной структурированной сетке

Традиционно конечно элементные методы на основе метода Галёркина для решения гиперболических и параболических уравнений строятся на неструктурированных сетках [1;  2]. Но немаловажный интерес представляет использование структурированной ортогональной сетки, в частности, при решении задач на локально-адаптируемых сетках. Рассмотрим двумерное уравнение переноса:

в области П = [0; 1] X [0; 1] с соответствующими начальными и периодическими граничными условиями.

Введем в области П структурированную прямоугольную сетку ^ , и в каждой ячейке л зададим базис {^к}к=0 из пространства полиномов степени не выше к . Приближенное решение системы (1) в ячейке л будем искать в виде [1]:

u_h(^x’t) = ^o^kCO^kW.                    (2)

Коэффициенты :;;<:■ в (2) найдем из условия ортогональности всем базисным функциям невязки, получаемой после подстановки (2) в (1):

Л _ — .^лт-- - , _ з-зз _ - - ■ -   = : - = :   . -          (3)

Далее получим

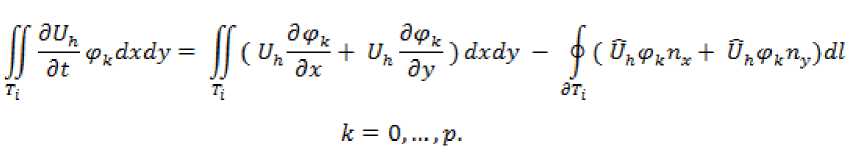
Обозначив за Зи матрицу масс, составленную из значений скалярных произведений базисных функций, за -:. С':. : - правую часть, получим систему:

^=ЖЯ

Выпишем расчетные формулы для ячейки ■ . Пусть К = _, рассмотрим следующий базис:

_   = - ..\ = Т - А. Т- =   . -   ; ,(5)

где .. . .. . - координаты центра ячейки.

Тогда приближенное решение принимает вид:

^■. = -< --<■<- ^з - -<у - з^(6)

Подставляя (6) в формулы (3) - (4), получим следующие системы уравнений:

Ят. 1Т ’ ldxdy + Я^ div^ ■1 dxdy = 0

Яг. ~^"(.х~ xc)dxdy + Яг. div^h ■ О - xc) dxdy = °

Яг. ^'(У~ yjdxdy + Ял div^ ■ (у - Ус) dxdy = 0

Далее получим iu0          dur                    du2 ff

— I dxdy + —— i (x - xc) • 1 dxdy + -— (y - yc) ■ 1 dxdy

J J          dt J J                      dt J J

Ti                  Ti                                 Ti

+ j(U_hln_x+ U_h-l-n_y)dl =0 dli

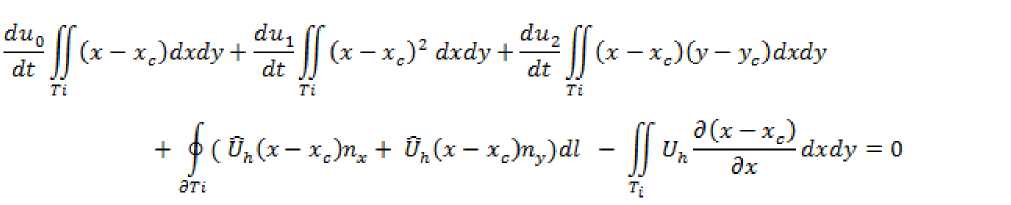
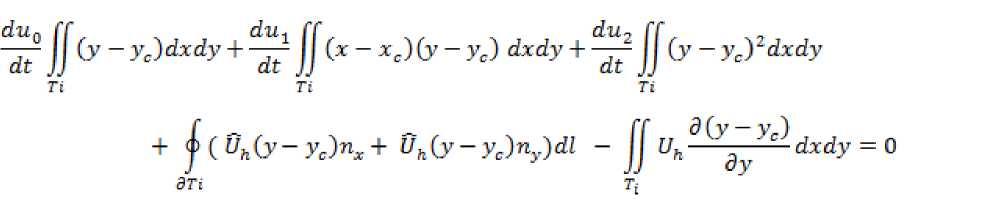
Тогда система (4) принимает вид:

M^ = dt

/            fdTi(Uh-l-nx+ Uh-l-ny)dl            \

$dTi(°h(^X~^XJⁿx+ U_h(x ~ xjnjdl - Я_г. Uh ^g^ ^dxdy \&_n( U_h(y- y_c)n_x + u_h(y- y^n^dl - Я_т. U_h ^^dxdy J

Дискретизация по времени осуществляется методом Эйлера, что приводит к явной схеме:

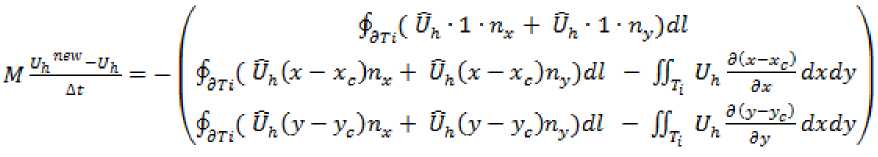
Была выполнена серия расчетов для определения порядка сходимости. Решалось уравнение (1) с начальными условиями следующего вида:

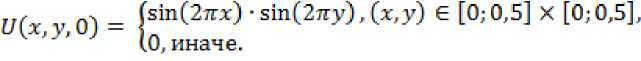
Решив систему (8) получим значение приближенного решения Uh .Зная точное решение U уравнения (1) найдем следующие нормы погрешностиr= Uh-U

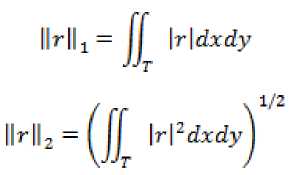
Порядки сходимости исследуемого метода будем определять по правилу Рунге:

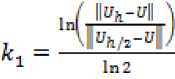
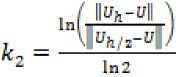
Таблица 1

Порядок сходимости

N	ML	Ml2		^2
25	0,010233	0,029926	-	-
50	0,002775	0,009574	1,8826694842	1,6442057456
100	0,000762	0,003231	1,8646248686	1,5671410555
200	0,000223	0,001125	1,7727472876	1,5220557492

Представленные результаты показывают, что рассмотренная методика позволяет получать решения с порядком сходимости выше первого на структурированных прямоугольных сетках. Что позволяет сделать вывод о применимости разрывного метода Галеркина для решения задач на блочных структурированных локально-адаптируемых сетках.