О применении WENO-схем к моделированию реагирующих газовых потоков

Введение. В настоящее время широкое распространение получило исследование газодинамических течений в задачах химической промышленности, поскольку технологам для получения целевых продуктов необходимо знать большое количество параметров проведения реакции. Наиболее значимым методом исследования стало математическое моделирование, которое позволяет рассмотреть поведение различных реакций в разных условиях без проведения лабораторных экспериментов. Аппарат математического моделирования расширяется и улучшается в прямой зависимости от появления новых задач: создаются новые математические модели, эффективные вычислительные алгоритмы, повышается точность расчетов. Настоящая работа направлена на исследование применения схем высокого порядка точности (WENO-схема 5 и 7 порядка) к решению задач многокомпонентной газовой динамики с учетом вязкости, диффузии, теплопроводности и химических реакций.

Математическая модель и численный алгоритм. Поскольку нас интересует исследование возможности повышения порядка точности расчетов с помощью WENO-схем, в настоящей работе мы рассматриваем одномерную модель уравнений вязкой дозвуковой динамики химически активной газовой смеси:

dU d(F(U)- H(U) dt ⁺       дх

= W(U).

Векторы U, F(U) H(U) W(U) имеют следующий вид:

(pYm\       / puYm\        (jr U = l pu  ,F(U)=   pu 2  ,H(U)= Г \ ph /         \ phu /          \q /pYm\  , .  puYmm\        jjr U = \pu  ,F(U)=   pu 2  ,H(U)= Г \ ph /         \ phu /          \q

'x), W(U) = ( 0 m ). "x\   ,     RRm\ ,xl.W(U) = ( 0 1. ' x /             0 0 /

В этой системе уравнений т = 1,... ,М, М - число компонент в газовой смеси, р - плотность смеси, Ym- массовая доля - ой компоненты смеси, и - скорость, h - энтальпия смеси, Jmx -диффузионный поток, Rm - скорость образования или расхода т - ой компоненты смеси, п =

Р — Р 0 - динамическая составляющая давления, р ₀ - термодинамическая составляющая давления, постоянная в области, T _xx - вязкий поток, q _x - потока тепла.

Система дополняется условием на дивергенцию вектора скорости:

4^ = -1- ( У' АУТ + У pDm,mix^YmVhm ^У^Ч*' Р»т,т1х™т) рСрТ\         Z-i    ,           I  p^i^m,,

\          mmm

+ -У ( Mwh

) ^Rm .

⁺ p ^y \M _Wm   С _р Т

m

Здесь С _р - теплоемкость смеси при постоянном давлении, Т - температура смеси, А -теплопроводность смеси, D _m,_mix - коэффициент диффузии, h _m - энтальпия образования компоненты смеси, M _w - молекулярная масса смеси, M _wm - молекулярная масса компоненты смеси. Более подробно математическая модель представлена в работе [1].

Для построения вычислительного алгоритма используем равномерную сетку отрезков: ^ △ x   { △ i , i 1, ., ^N , △   ^[x i-i , ^х ; ]> |^ i l ^xi   ^Xi—1   ^hx , ^hx^Nx    ^ x^}

Численный алгоритм строится по схеме расщепления по физическим процессам [2]. На первом этапе в этом расщеплении решается система уравнений химической кинетики, на втором этапе интегрируются уравнения законов сохранения без учета давления, далее рассчитывается поле поправок к давлению из решения уравнения Пуассона, на последнем этапе корректируются поле давления и поле скорости [2]. Поскольку мы исследуем применение WENO-схем, приведем подробно алгоритм второго этапа. Для интегрирования законов сохранения используется разностная схема вида:

Ц^ ¹ - Ц?  ^Pi+1/2 - ^Pi-1/2 _ ^Hi+1/2 - ^Hi-1/2 _ ₀

△ t              h _x                 h _x           ’

Здесь H i₊₁/₂ , H _i-1/₂ - диффузионные, вязкие и тепловые потоки на границе i и i + 1, i — 1 и i ячейками соответственно, которые рассчитываются по схеме с центральными разностями,

Pi+1/2, Pi-1/2 — конвективные потоки на границе i и i + 1, i — 1 и i ячейками соответственно, которые рассчитываются с использованием потоков Русанова [3]:

Pi+1/2 = 0.5 (P(ur+1/2) + РЩ+иг) — «Щ+1/2 — Uw))-а = тах(1и1+1/21,1и{+1/21), где U[+1/2 и Ul+1/2 - значения вектора переменных U справа и слева от границы между i и i+1 ячейками, которые рассчитываем с использованием WENO схем 5 и 7 порядка точности [4; 5].

Их суть заключается в следующем. Для нахождения значения вектора переменных U справа и слева от границы между i и i+1 используется выражение:

к

U i+1/2 = £ а™ №,?

v=1

Здесь К = 3 для случая схемы 5-го порядка, К = 4 для схемы 7-го порядка точности, H ^(v) -оптимальные весовые коэффициенты, U (Vi/₂ — значение на границе, полученное на шаблоне

^S   {^ i-v , ---’Хь -■, X i-v+K-1 }:

к-1

(vi ui+1/2

^ "   ^cvp ^ i-v+p .

р=0

В случае использования весовых коэффициентов с индикаторами гладкости значения вектора переменных U справа и слева от границы между i и i+1 находятся из выражения:

К

ч                ^(v)                  a(v)

^ ^Ui+1/ 2 , ^ = ^«^(yy^ = [_e + _IS(yy]p- v=1                      ^v=1

Здесь IS(v  - это индикаторы гладкости, г - некоторое малое число, вводимое, чтоб предотвратить деление на ноль. Величины cvp, Q(v\ IS(v) для К = 3, К = 4 приведены в работах [4; 5].

Вычислительные эксперименты. Рассмотрим следующую одномерную постановку задачи. Размер области 0.2 м, шаг по пространству 2 • 10-3 м, шаг по времени 1 • 10-5 с, расчет ведем до 0.2 секунд. Принимаются следующие начальные данные: в области от 0 м до 0.1 м температура газа 800⁰С; в области от 0.1 м до 0.2 м температура газа 1200⁰С; скорость потока 0.1 м/c; давление 101325Па; состав газовой смеси – метан 100% (CH4). Граничные условия: на границе слева со скоростью 0.1 м/c втекает метан с температурой 800⁰С, на границе справа задаются условия вытекания. Такая постановка задачи принята для того, чтобы выяснить какая из схем будет лучше считать в области перепада температур. В этой же области начнут происходить интенсивные реакции с расходом метана и образования продуктов реакции.

Рассматриваем 3 варианта расчета значений вектора U на границе ячеек: 1) схемой первого порядка точности, т.е. U [₊₁/₂ = U _i+1 , U ■₊₁/₂ = U , ; 2) WENO схемой 5-го порядка аппроксимации; 3) WENO-схемой 7-го порядка аппроксимации. На рисунках 1 и 2 представлены распределения температуры и метана. Из графиков можно сделать вывод, что схема первого порядка аппроксимации сглаживает решение в областях резкого изменения газодинамических параметров, разница температур составляет величину 10⁰С. Такой результат является достаточно большим расхождением в случае проведения лабораторных экспериментов. Расчет по схемам WENO 5-го и 7-го порядка практически совпадает, что говорит о преимуществе схемы WENO5, поскольку она использует более компактный шаблон. На рисунках 9 и 10 представлены расчеты по WENO-схемам с оптимальными весами и с расчетом индикаторов гладкости. Из графиков можно сделать вывод, что для рассматриваемых задач использование WENO-схем с оптимальными весами является преимущественным, поскольку графики полностью совпадают, а они являются менее трудоемкими. Полученный результат полного совпадения графиков можно объяснить преобладанием диффузионных процессов над конвективным переносом.

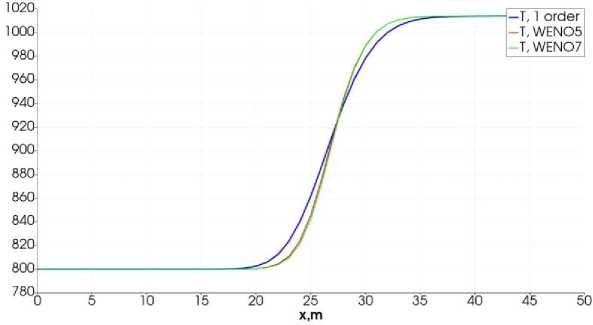
Рис. 1. Распределение температуры. Расчет по схемам 1-го порядка (синяя линия), WENO5 (красная линия), WENO7 (зеленая линия).

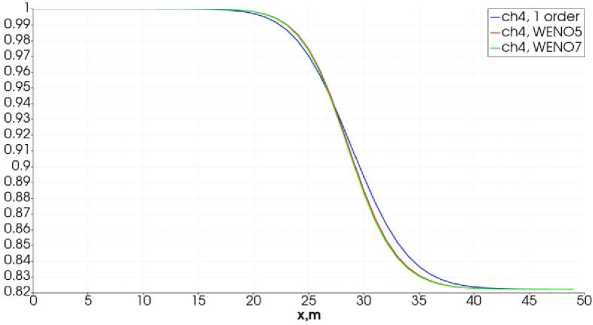
Рис. 2. Распределение метана. Расчет по схемам 1-го порядка (синяя линия),

WENO5 (красная линия), WENO7 (зеленая линия).

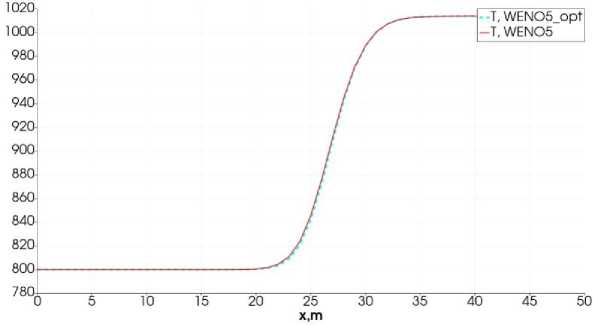
Рис. 3. Распределение температуры. Расчет по схеме WENO5 (красная линия) и схеме WENO5 с оптимальными весами (бирюзовый пунктир).

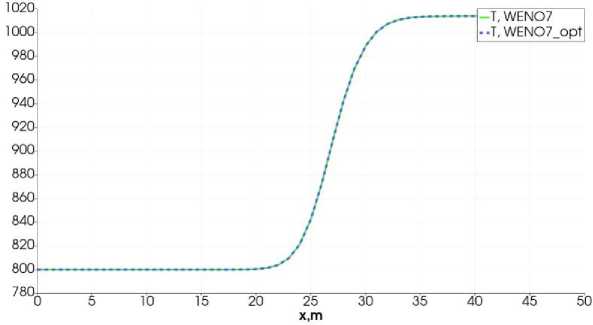
Рис. 4. Распределение температуры. Расчет по схеме WENO7 (зеленая линия) и схеме WENO7 с оптимальными весами (синий пунктир).

Выводы. В работе проведено исследование применения WENO-схем 5-го и 7-го порядка точности с оптимальными весовыми коэффициентами и с весовыми коэффициентами, рассчитанными с использованием индикаторов гладкости к задачам многокомпонентных реагирующих течений с вязкостью, диффузией и теплопроводностью. Показано, что по сравнению со схемами первого порядка точности WENO-схемы меньше сглаживают решение в областях резкого изменения газодинамических параметров и концентраций компонент смеси. Сравнение результатов вычислительных экспериментов, в которых весовые коэффициенты в WENO-схеме принимались оптимальными и рассчитывались с индикаторами гладкости показало, что результаты расчетов совпадают. Таким образом, можно сделать вывод о преимуществе использования оптимальных весовых коэффициентов в WENO-схеме, поскольку в данном случае алгоритм является менее трудоемким.