О природе параметра уравнения Енкеля для вязкости стеклообразующих жидкостей

Сандитов Д. С., Дармаев М. В., Машанов А. А. О природе параметра уравнения Енке-ля для вязкости стеклообразующих жидкостей // Вестник Бурятского государственного университета. Химия. Физика. 2019. Вып. 1. С. 3–8.

Отсутствие общепризнанной теоретической формулы для своеобразной температурной зависимости вязкого течения стеклообразующих жидкостей привело к появлению серии эмпирических соотношений [1]. Меерлендер [2] в результате сравнения наиболее распространенных пяти уравнений вязкости [Vogel-Fulcher-Tamman (1921–1925), Waterton (1932), Jenkel (1939), Bradbury (1951), Cornelissen и др. (1957) [1]] с опытными данными приходит к заключению, что уравнение Енкеля (Jenckel) [3]

П = A exp

BC

+ exp

TT

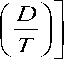
наилучшим образом описывает вязкое течение стеклообразующих жидкостей в широком интервале температуры.

Настоящее сообщение посвящено обсуждению природы постоянной этого уравнения D в рамках модели делокализованных атомов [4], что может дать определенную информацию о вязком течении и стекловании жидкостей.

Вывод уравнения Енкеля (1) с привлечением развиваемой модели позволяет связать эмпирический параметр D с энергией делокализации атома ∆ε e (k — постоянная Больцмана) [5, 6]

ДЕ = kD

Энергия ∆ε e выражается через температуру стеклования T g и долю флуктуационного объема f g , замороженную в области температуры T = T g [4],

Д=. = kT, ln(V f» )

Величина fg определяется по данным о вязкости и слабо зависит от природы стеклообразных систем; у аморфных веществ одного класса она практически постоянна [4]

f g =

Д V e

V

® const

T = T g

Флуктуационный объем ∆ V e обусловлен тепловыми смещениями (делокализацией) атомов: ∆ V e = N e ∆v e , где N e — число делокализованных атомов, ∆v e — элементарный флуктуационный объем, необходимый для предельного смещения атома (объем делокализации атома).

Расчет ∆ε e по формуле (2) из данных об эмпирической постоянной D = 2500 K [2] для силикатного стекла ( R — газовая постоянная)

Де = RD = 21 кД^ / моль находится в согласии с результатами расчета по уравнению модели (3) для ще-лочносиликатных стекол [4]

Д е = RT_g ln ( y f ) ~ (19 - 23) кДж/моль .

Из соотношений (2) и (3) при f g ≈ const следует, что параметр D должен быть пропорционален температуре стеклования ( D ~ T g )

^D = l ln ⁽y fg, ^{) ]} T g .                           (5)

На основе данных о температурной зависимости вязкости [7] мы определили значения D для ряда неорганических стекол и проверили линейность зависимости D от Tg. Как и следовало ожидать, у силикатных и германатных стекол пара- метр D действительно линейно зависит от температуры стеклования Tg (рис. 1 и 2). Однако прямые D — Tg у этих стекол не проходят через начало координат. Развиваемое представление можно привести в соответствие с экспериментом, если в соотношение (5) введем эмпирическое слагаемое D0 физический смысл которого остается не совсем ясным и требует в дальнейшем детального рассмотрения. Ниже ограничимся одним из возможных вариантов его интерпретации, согласно которому D заметно больше D0.

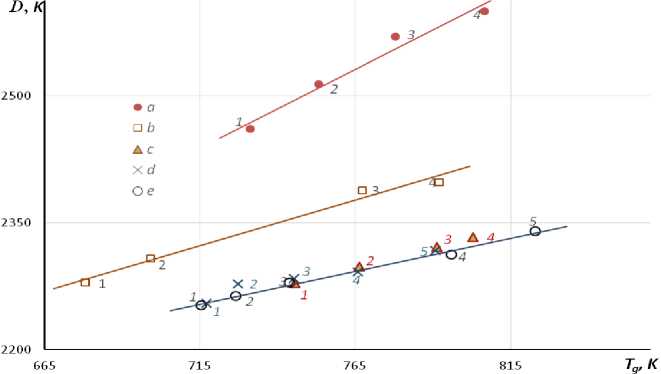
Рис. 1. Линейная корреляция между эмпирическим параметром уравнения Енкеля D и температурой стеклования T g для двухкомпонентных силикатных и германатных стекол при различных содержаниях окислов.

a — GeO 2 –Na 2 O (содержание Na 2 O, мол. %: 1 — 30, 2 — 25, 3 — 20, 4 — 15); b — SiO 2 –PbO (PbO, мол. %: 1 — 50, 2 — 45, 3 — 30, 4 — 24,6); c — SiO 2 –K 2 O (K 2 O, мол. %: 1 — 25, 2 — 20, 3 — 15, 4 — 13); d — SiO 2 –Na 2 O (Na 2 O, мол. %: 1 — 33, 2 — 30, 3 — 25, 4 — 20, 5 — 15); e — SiO 2 –Li 2 O (Li 2 O, мол. %: 1 — 33,3, 2 — 30, 3 — 25, 4 — 14, 5 — 10).

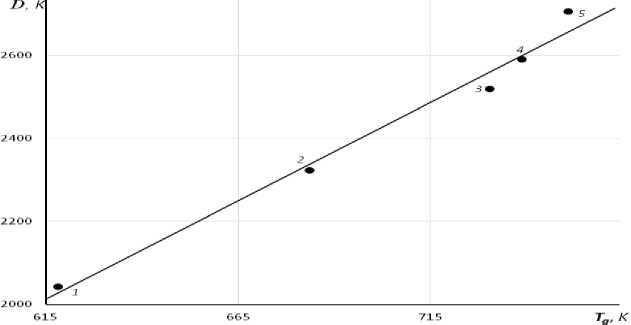
Рис. 2. Линейная корреляция между эмпирическим параметром уравнения Енкеля D и температурой стеклования T g для двухкомпонентных натриево-боратных стекол при различных содержаниях окислов (содержание Na 2 O, мол. %: 1 — 10, 2 — 15, 3 — 20, 4 — 25, 5 — 30).

D = Н/ f_e ) J T g + D 0 ^,

Предположим, что делокализация атома — его предельное упругое смещение из равновесного положения — служит необходимым условием реализации элементарного акта вязкого течения. Без делокализации атома (пускового механизма текучести) невозможно вязкое течение. Поэтому замораживание процесса делокализации атома в области стеклования приводит к прекращению вязкого течения и к переходу расплава в стеклообразное состояние. Этот момент наступает тогда, когда энергия тепловых колебаний решетки, отнесенная к атому, становится равной или меньше энтальпии делокализации атома: (г/2)kT < AH, отку- да следует условие перехода жидкость — стекло

A H = ikT , e ₂ g

где i — число степеней свободы кинетической единицы, ответственной за стеклование, а энтальпия ∆ H e равна работе по предельному упругому смещению атома, совершаемой против внутреннего p i и внешнего p давлений (∆ε = p i ∆v e ) [4]

^He = (Pt + P)Av e = A^e + PAv e (8)

Критерий стеклования (7) с учетом (8) преобразуется в выражение

A^e = |kTg — PAVe ,                      (9)

откуда, принимая во внимание равенство (2), для параметра D приходим к уравнению прямой

^D = |T g — 1 P A v e ,                     (10)

которое идентично соотношению (6), где D 0 получает следующую трактовку

D 0

P ^{A V} e k

Знак минус в равенстве (10) означает, что внешнее давление p действует на поверхность системы снаружи во внутрь, а тепловое давление Pt = (z/2)kTg Ave — наоборот, изнутри системы навстречу p. Равенство (10) [или (9)] представляет собой фактически уравнение состояния — баланс давлений [1]: pi + p = pt. При постоянном атмосферном давлении p = const, параметр D0, согласно (11), является однозначной функцией величины ∆ve.

В силикатных стеклах «делокализация атома» представляет собой предельное смещение мостикового атома кислорода в мостике Si-O-Si, связанное с локальной упругой деформацией кремнекислородной сетки из валентных связей [4, 5]. Поэтому объем делокализации атома ∆v e у этих стекол определяется объемом мостикового атома кислорода. У стеклообразных систем одного класса ∆v e ≈ const.

Обращает внимание то обстоятельство, что у трех щелочносиликатных стекол SiO2 — MeO2 (Me = K, Na, Li) экспериментальные точки на рис. 1 ложатся практически на одну прямую. Это означает, что параметры уравнения прямой (6) для них одинаковы, откуда следует, что fg ≈ const и D0 ≈ const. В самом деле, значения fg и ∆ve у этих щелосносиликатных стекол примерно одинаковы [4]: fg ≈ const ≈ 0.025 — 0.028 и ∆ve ≈ const ≈ (4-5) Å3, откуда и D0 является постоянной величиной.

Внутреннее давление жидкостей и твердых тел p i , обусловленное силами межатомного (межмолекулярного) притяжения, существенно больше обычного атмосферного внешнего давления p ≈ 1 атм [1]. При малых p в сравнении с p i в равенстве (8) энтальпия ∆ H e приближается к энергии делокализации атома ∆ε e . Поэтому в данном случае вторые слагаемые в соотношении (9) и в равенствах (6) и (10) относительно малы.

Таким образом, эмпирическая постоянная D в уравнении Енкеля (1) оказывается тесно связанной с температурой стеклования T g . Обоснование указанного обстоятельства приводит к определенному критерию стеклования.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования РФ (грант № 3.5406.2017/8.9).