О природе связи коэффициента поперечной деформации с неупругими характеристиками твердых тел

Коэффициент поперечной деформации (коэффициент Пуассона) µ определяется отношением поперечной деформации тела ε z = Δ d / d 0 к его продольному удлинению ε x = Δ l / l 0 при одноосном растяжении

A

£

z

£

x

и прежде всего характеризует приращение объема тела при одноосной деформации

К V

= ^£ x ( 1 -

2 A ) ^.

По определению параметр Грюнайзена γD выражает изменение частоты колебаний решетки в зависимости от изменения объема и обычно вычисляется из экспериментальных данных о коэффициен- те объемного теплового расширения β, адиабатическом модуле объемного сжатия ВА, молярной массе

µ, плотности ρ и молярной теплоемкости Cp вВ a A .

P C p

Y d

Он служит характеристикой ангармонизма колебаний решетки и нелинейности силы межатомно- го и межмолекулярного взаимодействий [1-6]. Принято считать, что гармонические и ангармониче- ские коэффициенты в разложении потенциальной энергии решетки по деформации являются независимыми параметрами [6]. Однако недавно [2] установлено, что ангармонический параметр Грюнайзе- на является однозначной функцией гармонической величины µ – параметра линейной теории упругости

3 ( 1 + A ) Y n = — I ------— I .

^D 2 ( 2 - 3 a )

Для многих металлов, ионных и молекулярных кристаллов оценка γ _D по этой формуле находится в первом приближении в удовлетворительном согласии с результатами расчета по уравнению Грю-найзена (1). Ранее были получены несколько иные варианты взаимосвязи между величинами γ D и µ [7, 8].

Настоящая работа посвящена дальнейшему исследованию связи коэффициента поперечной деформации с параметром Грюнайзена другими нелинейными неупругими свойствами кристаллических и стеклообразных материалов.

Результаты расчетов

С целью детальной проверки соответствия формулы Беломестных-Теслевой уравнению Грюнай-зена мы построили график зависимости γ D от функции коэффициента Пуассона (3/2)(1 + µ) / (2 – 3µ) для различных кристаллов. Сплошной линией на нем (рис. 1) представлена теоретическая зависимость γ D (µ) в соответствии с формулой Беломестных-Теслевой (3). На эту линию – прямую ложатся экспериментальные данные (светлые кружочки) в основном щелочногалоидных кристаллов с решеткой типа ионного кристалла NaCl, которые характеризуются преимущественно квазиизотропной структурой и центральными силами взаимодействия частиц (группа тел I). Данные для второй группы кристаллов с заметной анизотропией располагаются на пунктирной прямой, проходящей ниже теоретической прямой, практически параллельно последней. Таким образом, по отношению к данной зависимости рассмотренные кристаллические твердые тела делятся на две группы.

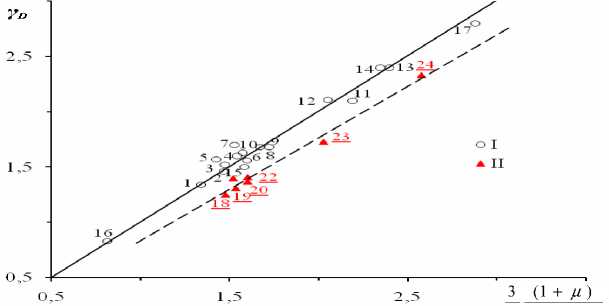
Рис.1. Зависимость параметра Грюнайзена у D от (3/2)(1+«)/(2-3^) для различ*2™2 „ р.~ )аллов. Использованы данные [1, 2]. Группа I: 1- LiF, 2- NaCl, 3- LiCl, 4- KCl, 5- NaF, 6- NaBr, 7- LiBr, 8- KBr, 9- Fe, 10- KI, 11- Co, 12- Al, 13- Ag, 14 - Pd, 15- RbBr, 16- Be, 17- Au; Группа II: 18- Y, 19- NaNO 3 , 20- NaClO 3 , 21- Th, 22- Mg, 23- Ta, 24-

AgBr

Для кристаллов, приведенных на рис. 1, были использованы значения γ _D , вычисленные по уравнению Грюнайзена (2) [1, 2]. Для стекол не всегда удается найти необходимые данные о величинах, входящих в это уравнение, особенно данные о тепловых характеристиках β и C_V . Поэтому для них вместо (2) мы пользовались формулой Леонтьева [9]

3 I B а | ,

A

/ D

² I P V k )

где v_K – среднеквадратичная скорость, которая не зависит от направлений распространения акустических волн,

2 v 2 + 2 v 22 v 2 = —-------,

K 3

v_L и v_S – скорости продольной и поперечной звуковых волн .

С помощью этой формулы для десяти различных стекол были рассчитаны параметры Грюнайзена и построены аналогичные графики в соответствии с соотношением Беломестных-Теслевой (3). Установлено, что все исследованные стекла хорошо описываются данным соотношением. В качестве примера на рис. 2 приводится рассматриваемая зависимость для натриевоалюмосиликатных стекол с различным содержанием окислов Na 2 O, Al 2 O 3 и SiO 2 . Как видно, экспериментальные точки ложатся на теоретическую прямую с тангенсом угла наклона, равным единице.

Представляют интерес другие варианты зависимости параметра Грюнайзена от коэффициента поперечной деформации, которые дают возможность высказать определенные суждения о природе этой зависимости γ D (µ) [10]. С этой целью обратимся к подходу Берлина-Ротенбурга-Басэрста [11], где дается анализ механического поведения ансамбля случайно упакованных сферических частиц, линейноупруго взаимодействующих друг с другом в месте контакта взаимно перпендикулярными силами: нормальными к плоскости контакта (центральными) f_L и тангенциальными (силами трения) f_S . Эти силы пропорциональны соответствующим смещениям ( x L и x S ) от положения равновесия f L = k L x L и f S = k S x S , где k_L и k_S – нормальная и тангенциальная жесткости.

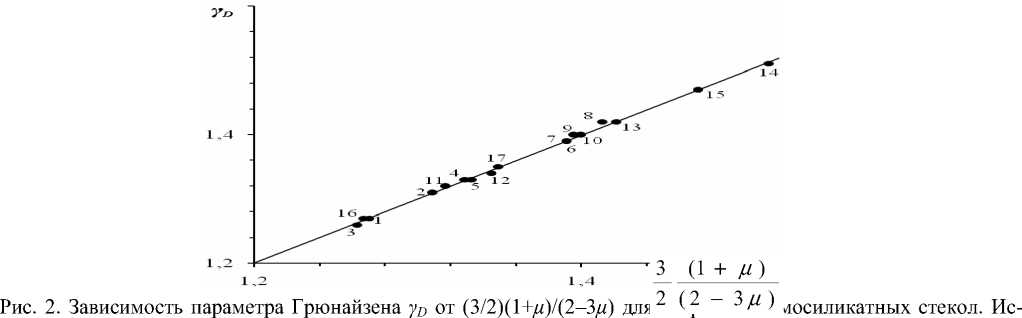
пользованы данные [25]. Содержание Na₂O/Al₂O₃/SiO₂, мол.%: 1- 15/0/85, 2- 15/5/80, 3- 15/10/75, 4- 15/15/70, 5 15/20/65, 6- 15/25/60, 7- 25/0/75, 8- 25/5/70, 9- 25/10/65, 10- 25/15/60, 11- 25/25/60; 12- 25/25/50, 13- 25/30/45, 14 35/0/65; 15- 30/5/65, 16- 20/15/65, 17- 17.5/17.5/65

Для такой системы коэффициент поперечной деформации µ определяется отношением этих жесткостей λ = k S / k L [11]

1 - 2

•

^{A _} 3  7

4 + 2

Подставив ц из данного соотношения в формулу Беломестных-Теслевой (3), приходим к заключению, что параметр Грюнайзена является функцией параметра 2

_     3

^Y D "" 2 (1 + 2 )

•

Мерой отношения тангенциальной (сдвиговой) и нормальной (изгибной) жесткостей межатомных связей, на наш взгляд, может служить отношение квадратов скоростей поперечной и продольной звуковых волн

2 = k kL

G

E

P v S Р v L

^v S , v L

где G - модуль сдвига, Е - модуль одностороннего растяжения [12, 13], E = B A + (4 G /3). В свою очередь, из известной формулы молекулярной акустики, устанавливающей связь между коэффициентом Пуассона и скоростями звука v_L и v_S , для отношения ( v_L ² / v_S ² ) следует выражение

vL vS

_ 2(1 -

A ) •

(1 — 2 A )

Принимая во внимание равенства (7) и (8), соотношение (6) можно представить в виде следующей функции у D (и)

_Y _ 3(1 - a ) .

(3 - 4A)

Как и следовало ожидать, данная зависимость оказывается линейной (рис. 3 и 4)

Y D

C 1

3(1 - A ) (3 - 4 a )

+ C ₂ ’

где С 1 и С₂ - эмпирические постоянные. Например, у натриевоалюмосиликатных стекол С 1 ~ 6.2 и С₂ ~ 5.5. Этот результат свидетельствует об оправданности в определенной степени модели Берлина-Ротенбурга-Басэрста при рассмотрении взаимосвязи между у _d и и.

Таким образом, с этих позиций можно предположить, что одной из причин тесной взаимосвязи между у_D и и может служить их зависимость от отношения сдвиговой и изгибной жесткостей межатомных связей.

О природе связи а с неупругими свойствами твердых тел . Коэффициент поперечной деформации как параметр теории упругости не должен быть связан с нелинейными неупругими свойствами твердых тел. Тем не менее из экспериментальных данных следуют вполне определенные корреляции между величиной и и пластической деформацией металлов [14] и стекол [15], между и и температурой размягчения стекол [16], а также между и и фрагильностью - характеристикой вязкости этих систем в области стеклования [17]. По-видимому, тот факт, что коэффициент Пуассона определяется деформациями, происходящими во взаимно перпендикулярных направлениях, выражает своеобразную зависимость и от интенсивности развития процессов неупругости в реальном деформируемом теле

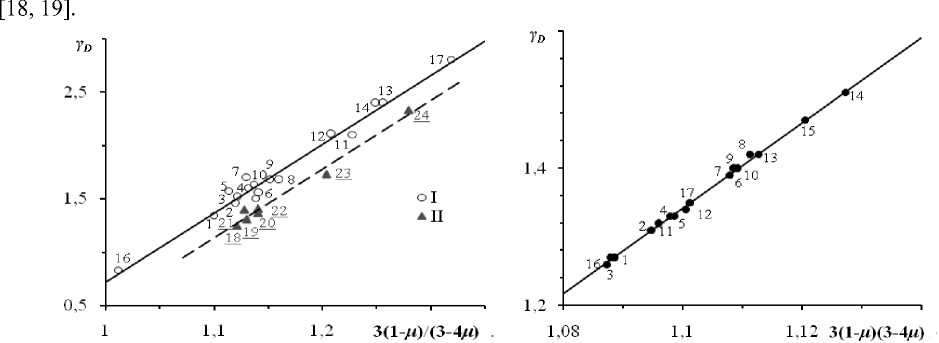
Рис. 3. Зависимость уD от 3(1-д)/(3-4д). Номера точек Рис. 4. Зависимость уD от 3(1-д)/(3-4д) для на-соответствуют номерам твердых тел на рис. 1          триевоалюмосиликатных стекол. Номера точек соответствуют номерам стекол на рис. 2

В этом отношении интересна связь коэффициента поперечной деформации с так называемой размерностью областей локализации и диссипации энергии, запасаемой деформируемым телом за счет работы внешних сил [20, 21]

₌ 2 ( 1 - ц ) . (10) f ( 1 - 2 ц )

Это соотношение получено из следующих соображений. Поведение деформируемого тела зависит от процессов образования и эволюции диссипативных структур, обеспечивающих рассеяние энергии [21]. К особенностям таких структур относится существование универсальной иерархии пространственных масштабов (структурных уровней), что обусловлено фундаментальным свойством твердого тела - его сдвиговой устойчивостью, определяющей различие характерных пространственных масштабов областей локализации и рассеяния энергии, запасаемой деформируемым телом.

Отношение пространственных масштабов диссипативных структур соседних уровней, иначе, размерность областей локализации энергии D f , определяется соотношением [21]

D = L . = L = v l, (11) f L, L s v 2

где L l ~ pv_L ² - характерный размер областей локализации энергии, L_S ~ рv_S ² - характерный размер областей, в которых рассеивается энергия (за диссипацию энергии в деформируемом теле ответственны только сдвиговые напряжения [22]). Из соотношений (8) и (11) следует выражение (10) для D f .

Естественно предположить, что с ростом размерности областей локализации и диссипации запасаемой энергии D f будет возрастать ангармонизм колебаний решетки у D . В самом деле, зависимость параметра Грюнайзена от D f (и) - функции коэффициента Пуассона (10) для ряда кристаллов и стекол оказывается линейной (рис. 5 и 6).

Остается открытым вопрос: почему параметр линейной теории упругости - коэффициент Пуассона зависит от неупругих свойств твердых тел? Известны различные попытки выяснить природу коэффициента Пуассона. Однако сегодня приходится признать, что нет полной ясности относительно физического смысла этой величины [1-8, 10-19]. Теория упругости при строгом подходе справедлива только для идеальной изотропной сплошной среды. Для реальных твердых тел с неоднородными анизотропными структурами могут наблюдаться отклонения от выводов этой теории (рис. 1). В связи с этим вызывает интерес представление Кузьменко [18, 19] о процессе деформирования материалов. Он показал, что можно успешно рассмотреть ряд нерешенных проблем, оставаясь в рамках классической механики твердого деформируемого тела, если наделить однородную бесструктурную сплошную среду некоторыми свойствами реальных материальных систем. В теорию упругости он вводит понятие о противодействии системы ее деформированию, что позволяет по новому подойти к эффекту поперечных деформаций твердого тела.

Под противодействием или «реакцией» понимается ответное действие вещества (возникающее в результате перестройки структуры) в направлении обеспечения устойчивого существования системы в изменившихся условиях. Процесс деформирования делится на два этапа: первый, где ведущую роль играет внешнее воздействие, и второй, связанный с силами противодействия вещества. В отличие от третьего закона Ньютона здесь противодействие отделено от действия (хотя они и тесно связаны).

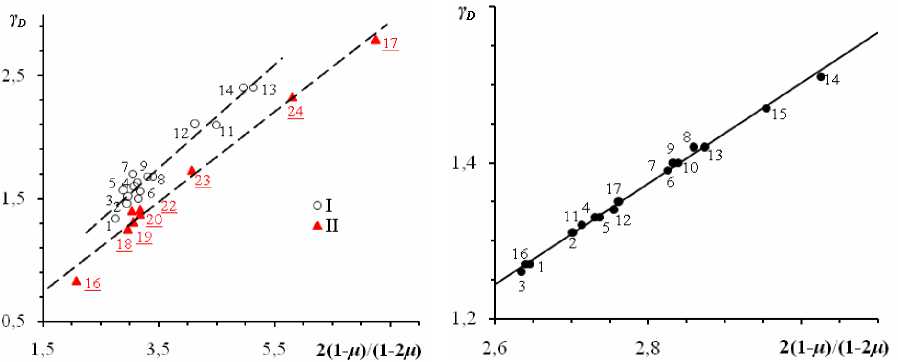
Рис. 5. Зависимость у D от 2(1-д)/(1-2д) для кристал- Рис. 6. Зависимость у D от 2(1-д)/(1-2д) для стекол. лов. Номера точек соответствуют номерам твердых Номера точек соответствуют номерам стекол на рис. 2 тел на рис. 1

Если изменение размеров вещества под действием, например, односторонних сил происходит в одном направлении, то изменение размеров тела под действием реакции всегда происходит всесторонне («гидростатически»). Кузьменко доказывает, что поперечные деформации, характеризующиеся коэффициентом Пуассона, обусловлены силами реакции и возникают лишь на втором этапе процесса деформирования. Коэффициент Пуассона отражает способность вещества противодействовать изменению объема. Например, большая величина µ означает способность материала эффективно компенсировать изменение объема, возникающее на первом этапе деформирования, так что чем больше µ, тем меньшей оказывается итоговая величина изменения объема твердого тела и тем меньшей должна быть энергия изменения объема. Верхний предел µ = 0,5 получается из условия, что изменение объема при деформировании компенсируется полностью реакцией вещества (1), при µ = 0,5, ΔV = 0). Это условие относится к жидкостям, а для твердых тел всегда µ < 0.5, ибо для них полной компенсации изменения объема не бывает. Установлено, что коэффициент поперечной деформации характеризует удельный вес энергии сдвига в общей энергии деформирования. Чем больше µ, тем меньше энергия сдвиговых деформаций, тем меньше сопротивление сдвигу оказывает данный материал, тем ближе он в этом отношении к жидкости (µ = 0,5) [18, 19].

С этих позиций коэффициент Пуассона вполне может быть связан определенным образом с такими неупругими свойствами материала, как предел пластичности (текучести) [15] и размерность областей локализации и диссипации энергии D f (µ), запасаемой деформируемым телом.

Материалы с повышенной мягкостью и пластичностью (золото, серебро, медь) имеют большие значения µ, приближающиеся к 0,5, а материалы с повышенной твердостью и хрупкостью (бериллий, стекла) имеют сравнительно небольшие значения µ, лежащие в пределах 0,20–0,30 [15]. Например, у твердого и хрупкого кварцевого стекла µ = 0,17.

С этой точки зрения становится понятной зависимость коэффициента Пуассона твердых тел от отношения сдвиговой и изгибной жесткостей межатомных связей λ, что определяется отношением квадратов скоростей распространения поперечной и продольной звуковых волн λ = v S ² / v L ² . В самом деле, в мягких материалах с большим значением µ скорость звука в поперечном направлении ( v_S ) оказывается существенно меньше, чем в продольном направлении ( v_L ). Большим значением коэффициента Пуассона (µ ≈ 0,40-0,45) обладают такие пластичные материалы, как золото, серебро, медь, характеризующиеся небольшими значениями λ ≈ 0,1-0,2, а низкое значение µ наблюдается у бериллия (µ = 0.034) с большим значением λ = ( v S / v L ) ² ≈ 0,5.

Недавно Пинеда [4] в рамках модели Кнута [23] рассмотрел влияние структурных изменений на коэффициент Пуассона металлических стекол. Потенциал межатомного взаимодействия в данной модели состоит из гармонической и ангармонической частей

U (r) = a (r –r0)2 – b (r –r0)3, где а – гармонический, а b – ангармонический коэффициенты, r0 – межатомное расстояние, соответствующие минимуму потенциала. Модель основана на предположении о Гауссовом распределении расстояния между ближайшими соседями (атомами) в идеальном однокомпонентном металлическом стекле. Предполагается, что упругие свойства определяются непосредственным окружением атомов – первой координационной сферой. Функция радиального распределения RDF(r) положения атомов в аморфном металле описывается соотношением

RDF

( r ) =

r

(2 п )^,/2

N' f

------I exp r i ^G i (

⁽ r ^- r 1 ^{) 2}

2 ^ 12

где r 1 и σ 1 – средний радиус и ширина первой координационной сферы, N 1 – число атомов в первой координационной сфере.

В окончательные формулы мгновенных модулей объемного сжатия В и сдвига G входят a , N 1 , r 0 , v at и безразмерные параметры

5 = ^ , r ₀

^ i

G = —L, r0

p

br ₀

a

где σ = ( r ₁ – r ₀), v_at = V / N – атомный объем. Величины s и σ описывают среднее отклонение атома от r ₀ и среднюю дисперсию вблизи этого значения, соответственно. Параметр р характеризует степень

ангармоничности потенциала.

Примечательно то, что такая простая модель находится в согласии с экспериментально наблюдаемым поведением упругих модулей В и G и их отношения B / G , которым определяется коэффициент Пуассона µ. Полученные результаты были использованы Пинедо для объяснения экспериментов по структурной релаксации (при уменьшении фиктивной температуры T f ) и по всестороннему сжатию металлических стекол. В обоих процессах плотность стекла увеличивается. Следовательно, уменьшается среднее межатомное расстояние, что приводит к возрастанию упругих модулей. Однако коэффициент Пуассона в результате структурной релаксации уменьшается (снижение параметра σ оказывается сильнее), но увеличивается при сжатии под давлением (здесь эффект уменьшения s явля-

ется доминирующим). В целом модель качественно правильно описывает изменения упругих характеристик в этих опытах.

Согласно полученным уравнениям, B и G напрямую зависят от числа атомов в первой координационной сфере N ₁, а отношение B / G не зависит от изменения N ₁. Это означает, что при структурной релаксации предсказываемое уменьшение коэффициента Пуассона µ происходит в основном за счет изменений параметра σ, но не из-за изменений координационного числа N 1 первого пика RDF. В соответствии с моделью упругие модули B и G пропорциональны гармоническому коэффициенту а – параметру межатомного потенциала, а их отношение B / G (следовательно, и коэффициент Пуассона µ) не зависит от а и определяется только параметром ангармоничности р.

Этот результат согласуется с однозначной зависимостью коэффициента поперечной деформации µ от параметра Грюнайзена γ – меры ангармонизма (3), а также с линейной корреляцией между γ и отношением скоростей продольной и поперечной звуковых волн ( v L / v S ) [24].

Заключение

Таким образом, как у кристаллических, так и у стеклообразных материалов между коэффициентом поперечной деформации и параметром Грюнайзена наблюдается вполне определенная взаимосвязь. Основной причиной существования такой взаимосвязи между этими величинами может оказаться их связь с отношением сдвиговой (тангенциальной) и изгибной (нормальной) жесткостей межатомных связей. Зависимость коэффициента Пуассона от неупругих свойств твердых тел можно объяснить, если его рассматривать как величину, характеризующую противодействие деформируемого тела изменению его объема.