О проблеме построения математических моделей для оптимизации параметров фрикционных демпферов на примере лопаток газотурбинных двигателей

Известно, что фрикционные демпферы используются как эффективный метод для снижения колебаний лопаток газотурбинных двигателей. Один из принципов действия ФД заключается в том, что под действием центробежной силы F Д демпферы ФД давят на полки, создавая силы трения, и приводят к снижению колебаний лопаток (рис. 1). Одной из важных проблем при проектировании ФД является оптимизация их параметров.

Рис. 1. Структура лопаток с фрикционными демпферами и виды демпферов

Для решения этой задачи прежде всего необходимо построить математическую модель, которая описывает динамические характеристики системы «ло-патка–ФД». Эта модель должна отвечать следующим требованиям:

– точно отображать динамические характеристики системы «лопатка–ФД».

– обеспечивать простоту решения динамических уравнений системы.

Построение полной математической модели состоит из следующих этапов.

Этап 1. Построение математической модели, которая отображает динамические характеристики лопаток без ФД.

Этап 2. Построение математической модели, которая отображает контакт между лопатками и ФД.

Этап 3. Построение системы математических уравнений, отображающих динамические характеристики системы «лопатка–ФД».

Этап 4. Построение алгоритмов для оптимизации параметров ФД.

Этап 5. Решение полученной системы математических уравнений.

Проблема этапа 1 состоит в необходимости исследования динамических характеристик лопаток. Имеется достаточно много работ по построению подобных математических моделей. Из них можно выделить модель пружинного маятника [1], балочную модель, пластинчато-оболочечную модель и др. В последние годы с развитием вычислительной техники широко используется модель конечных элементов. Согласно методу конечных элементов (МКЭ), в зависимости от формы лопатки можно применять двухмерные и трехмерные конечные элементы. Применение МКЭ для исследования колебаний лопаток газотурбинных двигателей показано в работе [2].

Особенность этапа 2 состоит в необходимости рассмотрения контактной задачи деформированных тел. Исследованию этой задачи посвящены работы [3; 4]. Самое обобщенное решение может быть получено при рассмотрении системы «лопатка–ФД» как единой механической системы. При этом необходимо решить два класса задач: статическую контактную задачу в зоне контакта между лопаткой и ФД и динамическую задачу системы. Результаты решения контактной задачи являются входными данными для решения динамической задачи. Однако эта модель требует очень большого количества вычислений, причем возникает проблема сходимости численных решений, поэтому в большинстве случаев такая модель будет неэффективна. Более эффективным может быть построение модели данной задачи в упрощенном виде на основе стандартных фрикционных демпферных элементов (ФДЭ) [5]. Работа [5] также показывает построение ФДЭ и моделирование режимов контакта по плоскостям или линиям через контактные дискретные точки. ФДЭ могут быть трехмерные или одномерные. Трехмерные ФДЭ используются, как правило, в трехмерных задачах. Однако в отдельных случаях использование таких моделей ФД нецелесообразно. Иногда более целесообразно использовать одномерные модели, чтобы уменьшить затраты компьютерного времени.

Такая модель (рис. 2) характеризуется следующими параметрами: жесткостью KД и максимальной силой трения FД = µN. Данная модель соответствует движению вида «макроскольжение» (рис. 3, а). Для модели с микроскольжением используются соотношения, показанные на рис. 3, б, в, г, д [6-8].

Для исследования колебания лопатки с ФД можно предположить, что скольжение является макроскольжением.

Для этапа 3, в соответствии с МКЭ, математическая система уравнений, отображающая динамические характеристики системы «лопатка-ФД» с N степенями свободы и N Д ФДЭ, имеет вид

[ M ] { X } + [ C ] { X } + [ К ] { x } + { f _ф } = { P ( t ) } , (1)

где [M], [C], [К] - обобщенные матрицы масс, вязкого демпфирования и жесткости; {X},{X},{x} - обобщен ные векторы узловых ускорений, скоростей и перемещений; {P(t)} - обобщенный вектор внешней динами ческой нагрузки; t - время; {/р} - обобщенный вектор силы трения (см. рис. 2);

F ¹

тр

F1

тр

^{ f _т н • •

. F N

Fтр =КД zj (t) = = ' Xj(t) - Xmjax + ZД при 0 < tot < a; = K- - Z Д при a < tot < n; Д Xj(t) + XPax - Z Д при n < tot < n + a; 73 Z Д при n + a < tot < 2n, где

F Д ^j

Z j = —Ч-, K j - жесткость j -го ФДЭ, F j - мак-

Д KД   Д                       Д симальная сила трения j-го ФДЭ. Для степеней свободы нет ФДЭ, Fj = 0 .

Система (1) состоит из N уравнений. Из них N Д уравнений являются нелинейными (в уравнениях присутствует трение) и ( N - N Д ) уравнений являются линейными (в уравнениях отсутствует трение). Решение системы (1) дает динамические характеристики системы.

На этапе 4 важной проблемой при проектировании ФД является выбор параметров ФД, к которым относятся форма, размеры, материал, масса и местоположение ФД на лопатке. Согласно одномерной модели ФДЭ (см. рис. 2), двумя важными параметрами ФД являются жесткость ФДЭ ( К д ) и максимальная сила трения ФДЭ ( F д ).

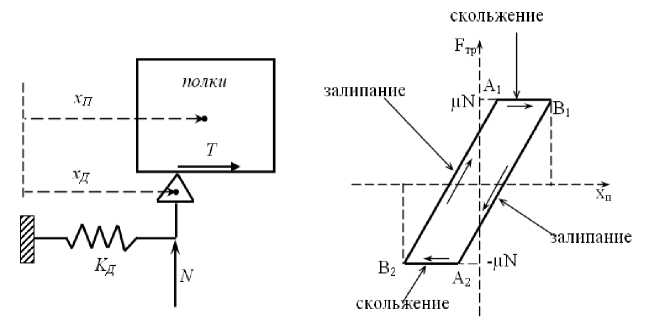
Рис. 2. Одномерная модель ФДЭ

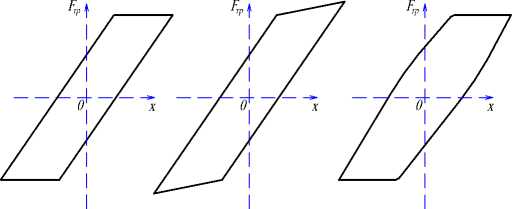
а                  б                   в

Рис. 3. Соотношения между силой трения и перемещением с макроскольжением ( а ) и с микроскольжением ( б , в , г , д )

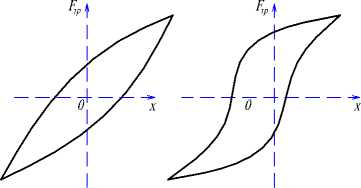
г                      д

Выбор K Д в общем зависит от характеристик материалов ФД, конструкции ФД, качеств поверхности ФД и полки лопаток в месте контакта, месте ФДЭ на конструкции и других факторов. Точное определение их значений является затруднительным. Для определения значения K Д необходимо рассмотреть статическую контактную задачу. Согласно работам [4; 9], значение контактной перпендикулярной жесткости должно быть подобрано так, чтобы обеспечить достаточную точность и сходимость результатов. Величина касательной жесткости имеет вид K τ ∈ [0,01 K N ; K N ], где K_N – перпендикулярная жесткость ФДЭ. Для большинства контактных задач величина K_N принимается на три порядка большей, чем максимальное значение жесткости соседних узлов. Много большее значение K N может отрицательно сказаться на сходимости процесса или даже привести к его дивергенции, а много меньшее значение K N может служить причиной некорректного результата. Увеличение значения K Д более чем на два порядка ( K Д >  K ·10²) не приводит к дальнейшему изменению амплитудно-частотной характеристики системы (рис. 4).

В работах [9; 10] представлен алгоритм для считывания значения K_N на каждом шаге вычисления, и в нашей задаче мы можем считать K Д = K τ . В работе [8] представлена модель для вычисления значения контактной жесткости по качеству поверхности ФД и полки лопаток. По мнению авторов этой статьи, при определении значения контактной жесткости можно выделить два случая: микроскольжение и макроскольжение. При микроскольжении значение контактной жесткости значительно зависит от качества поверхности ФД, а при макроскольжении – от жесткости конструкции. Они могут быть получены по соотношению между перемещением и нагрузкой. Схема определения значения K τ при макроскольжении показана на рис. 5, а при микроскольжении величина K τ детально описана в работе [8].

Выражение для определения K Д в любой точке А имеет вид

K = ^{δ F} , (3) Д _δ S

где δ F – сила, действующая в точке А; δ S – перемещение ФД в точке А по направлению силы δ F .

В программном комплексе ANSYS выполнен расчет δ S при δ F = 1 Н (см. рис. 5). Для расчета приняты следующие характеристики материала ФД: модуль Юнга E = 2,0·10⁵ МПа; коэффициент Пуассона µ = 0,3; плотность ρ = 7 700 кг/м³.

С учетом выражение (3) имеем:

– для трапециевидного демпфера:

KД =

δ F δ S

0,174 ⋅ 10 ^{- 7}

= 5,75 ⋅ 10⁷Н/м;

– для круглого демпфера:

KД =

δ F δ S

¹       = 4,329 ⋅ 10⁷Н/м.

0,231 ⋅ 10 ^{- 7}

Когда значение K Д определено, проблема оптимизации ФД рассматривается как оптимизация значения максимальной силы трения ФДЭ – F Д или массы ФД. Очевидно, что значение F Д должно быть принято таким, чтобы амплитуды колебания лопатки были минимальные. Для систем с одной степенью свободы можно легко определить оптимальное значение F Д по аналитическим выражениям [1]. Однако для модели лопатки по МКЭ (с большим числом степеней свободы) не может быть аналитического решения. Согласно работам [6–8; 11–13], задача оптимизации значения F Д решается определением амплитуд колебаний лопатки, при этом выбор значения F Д должен быть таким, чтобы значение амплитуд колебаний было минимальным. Рассмотрим результаты определения амплитуд колебаний на примере одной модели лопатки (рис. 6) с одним определенным условием нагрузки при различных значениях F Д ( F Д = 26, 30, 34, 38, 80, 150 Н). Для каждого значения F Д получим одну кривую частотно-амплитудной характеристики колебания верха лопатки. По этим результатам видно, что минимальные значения амплитуды колебаний получены при F Д = 38 Н. Можно сделать предположение, что для этой модели лопатки и условий нагружения оптимальное значение F Д равно 38 Н.

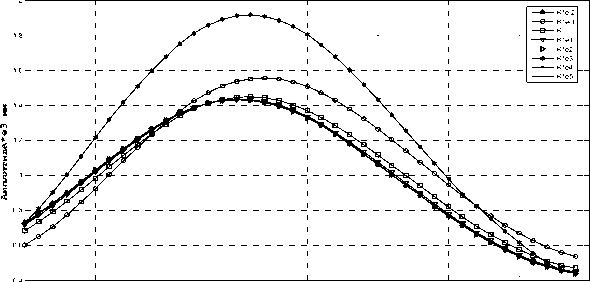
190                195                200

Частота-рад/с

Рис. 4. Влияние значения K Д на амплитуды колебания

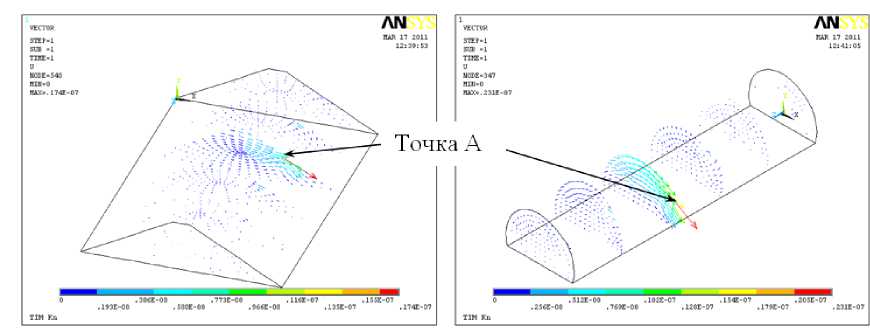
Рис. 5. Результаты определения δ S при δ F =1 Н

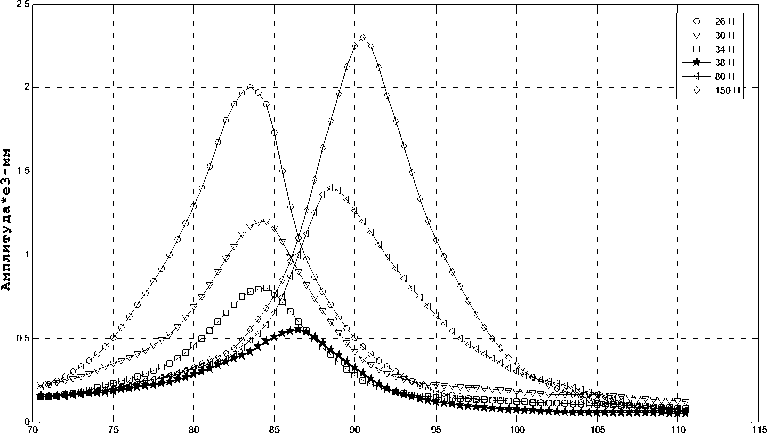
Частота-рад/с

Рис. 6. Влияние значения F _д на амплитуды колебаний

На этапе 5 необходимо решить систему уравнений (1). Для этого можно применить метод прямого численного интегрирования (ПЧИ) [14; 15], что требует больших затрат компьютерного времени. В отдельных случаях как эффективный метод для уменьшения затрат времени расчета использовался метод гармонического баланса (ГБ) [2; 14; 15]. Но для этой модели использование данного метода проблематично, так как функция силы трения задана не в явном виде.

Авторы этой статьи предложили метод гармонического баланса во временной области (ГБВО). Данный метод эффективен для уменьшения затрат времени расчета при решении системы уравнений (1) и может с успехом применяться при расчете реальных конструкций. При расчете конструкций со многими степенями свободы затраты времени расчета значительно уменьшаются.

Для определения оптимальных параметров фрикционных демпферов лопаток газотурбинных двигате- лей предлагается использовать схему (рис. 7), согласно которой необходимо корректно выбрать материал, форму ФД, вид соотношения между силой трения и перемещением и интервал изменения FД.

Материал ФД выбирается с учетом прочности ФД при тяжелых режимах работы двигателей и технологичности его изготовления. Форма ФД выбирается исходя из формы полки и диска (см. рис. 1). Вид соотношения между силой трения и перемещением принимается исходя из выбранного материала ФД, видов и значения перемещения ФД (см. рис. 3). Интервал изменения F Д выбирается на основе значения вынужденной силы.

Значение выбранной максимальной силы трения F Д определяется массой m ФД, коэффициентом трения µ, угловой скоростью ротора двигателя Ω и формой ФД в месте контакта. Когда значение µ, Ω и форма ФД выбраны, очевидно, что значение F Д зависит только от m и оптимизация F Д является также оптимизацией m .

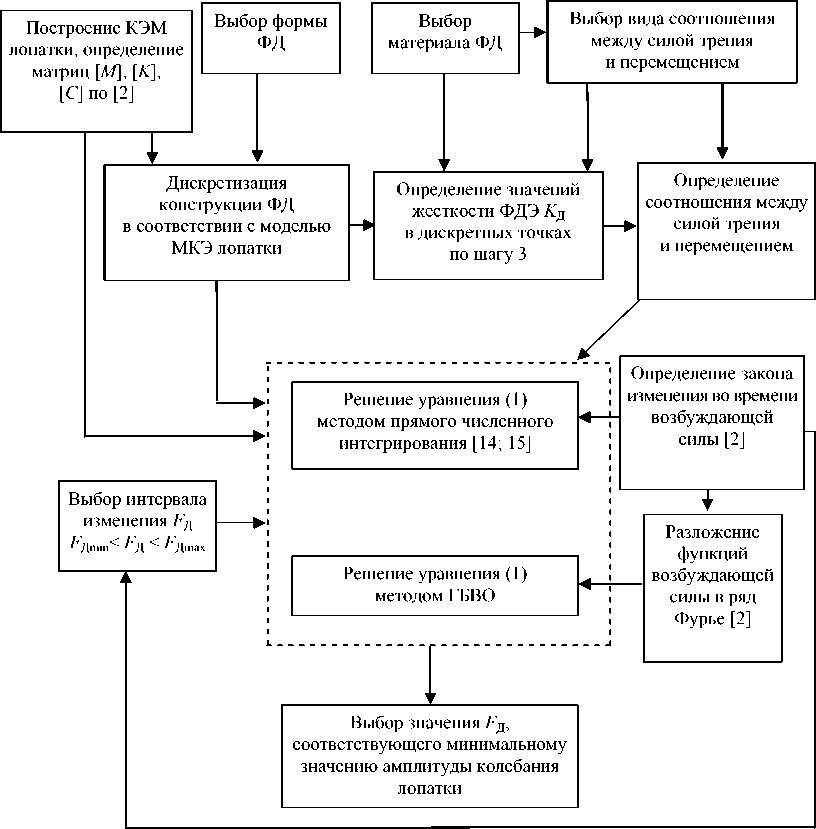
Рис. 7. Схема выбора значения F Д

Известно, что задачи проектирования ФД могут быть решены другими приближениями и имеют много решений. Однако проведенные исследования показывают, что задача оптимизации ФД сводится к задаче оптимизации значения максимальной силы трения F Д или массы ФД. По мнению авторов, это самое экономное приближение, потому что значение массы ФД легко изменяется и значительно влияет на работу ФД.

Использование этой схемы с моделированием режима контакта по плоскостям или линиям через контактные дискретные точки и стандартные фрикционные демпферные элементы и использованием метода ГБВО приводит к значительному уменьшению затрат времени расчета при проектировании ФД. Величина уменьшения затрат времени расчета зависит от количества степеней свободы системы: часто она в 10 раз меньше, чем при использовании метода прямого численного интегрирования и в 100 раз меньше, чем при совместном решении статической и динамической контактной задач. Точность методов почти совпадает. Поэтому, по мнению авторов, данная схема является эффективной и может быть использована для задачи проектирования ФД.